이 글은 칸아카데미-선형대수학 강의를 듣고 일부를 요약한 글입니다.

용어의 정의

1) 집합과 사상

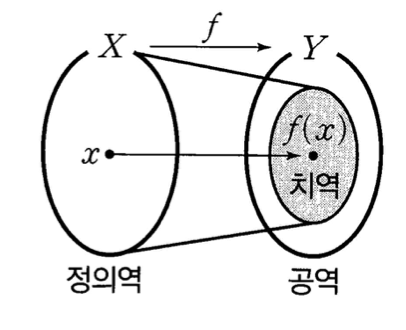
• 집합
  • 정의역 : 대응시키려는 집합 X
  • 공역 : 대응되는 집합 Y
  • 치역 : 정의역에 대응되는 공역의 원소의 집합
• 사상
  • 전사 : 공역과 치역이 동일한 사상
  • 단사(일대일 사상) : 정의역의 원소가 다르면 대응하는 상도 다른 사상
  • 전단사(일대일 대응) : 전사이면서 단사인 사상

2) 행렬

• 정방행렬 : 행과 열의 수가 같은 행렬 (행과 열의 수가 n인 행렬은 n차 정방행렬)
• 주대각 성분 : n차 정방행렬에서 (1,1) 위치부터 (n,n) 위치까지의 성분
• 대각행렬 : 주대각 성분을 제외한 모든 성분이 0인 행렬
• 단위행렬(항등행렬) : 주대각 성분이 모두 1이고 나머지 성분이 모두 0인 행렬
• 대칭행렬 : 본래의 행렬과 전치 행렬이 같은 행렬

벡터와 공간

선형 결합

X = c1x1 + c2+x2 + ... + cnxn 일 때, X를 벡터 x1,x2, ... ,xn의 선형 결합이라고 한다.
(V1에 대해 연산을 통해 만들어낸 Vn을 선형 결합이라고 함)

선형 독립/종속

선형 독립이란?
S = {x1, x2, ..., xn} 부분집합의 벡터 간 결합을 통해 부분집합의 다른 벡터를 만들 수 없는 경우.
(c1x1 + c2+x2 + ... + cnxn = 0 / c1 = c2 = ... = cn = 0 인 경우)

선형 종속이란?
부분집합의 벡터 간 결합을 통해 부분집합의 다른 벡터를 만들 수 있는 경우.
(c1x1 + c2+x2 + ... + cnxn = 0 에서, 상수(c1,c2,cn) 중 하나라도 0이 아닌 경우)

부분 공간 / 생성

부분집합 필요 충분 조건

• 덧셈에 닫혀 있어야 함
  (부분 집합 내 벡터 간 덧셈 결합 벡터는, 부분 집합에 포함되어야 함)
• 곱셈(스칼라배)에 닫혀 있어야 함
  (부분 집합 내 벡터의 스칼라 배 결합 벡터는, 부분 집합에 포함되어야 함)
• 0 벡터 포함

생성
W = span(S) ... S의 벡터 간 일차 결합으로 만들 수 있는 모든 벡터의 집합

기저 (basis)

기저 조건

• 집합 S는 선형 독립
• span(S) = Rn

※ S는 Rn의 기저(basis), 단 Rn의 기저는 여러 개.
T (표준 기저) = {[1 0], [0 1]}

벡터

벡터의 길이 (Norm)

벡터의 내적 (dot product)
내적의 결과 = scalar

※ 벡터 x, y 직교할 때 x, y 내적의 결과는 0

• 내적의 성질
  $\vec x \cdot \vec y \; = \|\vec x\|\, \|\vec y\|\,cos\theta \\ |\vec x \cdot \vec y| \le \|\vec x\|\, \|\vec y\| \\ \vec x = c\vec y, \quad (|\vec x \cdot \vec y| = \|\vec x\|\, \|\vec y\|)$

벡터의 외적 (cross product)
외적은 $R^3$(3차원 벡터)에서만 계산 가능
외적의 결과 = vector (주어진 벡터들의 직교 벡터)
※ $|\vec a \times \vec b|$ = $\vec a, \vec b$ 로 만들어진 사각형의 넓이

행렬

REF(행 사다리꼴) / RREF (기약 행 사다리꼴)

1. REF 성질
   1) 선분이 모두 0인 행은 행렬의 맨 아래에 위치
   2) 각 행에서 처음으로 나타나는 성분은 1 (= 선행성분)
   3) i행, i+1행 모두 선행성분이 존재하면 i+1행의 선행성분은 i행의 선행성분보다 오른쪽에 위치

   $\begin{bmatrix} 1\; 5\; 3\; 4 \\ 0\; 1\; 0\; 5 \\ 0\; 0\; 1\; 2 \\ \end{bmatrix} \quad \begin{bmatrix} 1\; 4\; 5 \\ 0\; 1\; 2 \\ 0\; 0\; 0 \\ \end{bmatrix}$

2. RREF 성질
   1) REF 성질을 모두 만족하고, 선행성분을 포함한 열은 선행성분 외 모든 성분은 0

   $\begin{bmatrix} 1\; 0\; 0\; 3 \\ 0\; 1\; 0\; 5 \\ 0\; 0\; 1\; 2 \\ \end{bmatrix} \quad \begin{bmatrix} 1\; 0\; 0 \\ 0\; 1\; 0 \\ 0\; 0\; 1 \\ \end{bmatrix} \quad \begin{bmatrix} 0\; 0\; 0\\ 0\; 0\; 0 \end{bmatrix}$

영공간 (Null Space)
(m x n 행렬) Ax = 0의 해공간
Ax = 0 첨가행렬의 RREF 구한 뒤, 기저와 차원 확인