자료구조 #2 순환(Recursion)

이 글은 이소연 교수님의 자료구조 강의를 듣고 정리한 내용입니다.

---

순환 알고리즘

1️⃣ 순환(Recursion)이란?

순환(Recursion)이란, 알고리즘이나 함수가 자기 자신을 다시 호출하여 문제를 해결하는 기법을 말한다. 아래의 적용 사례에서 자세히 다루겠지만, 팩토리얼(N부터 1까지의 곱셈 연산)과 같이 일정한 수 또는 패턴이 반복되는 경우에 적용할 수 있다.

2️⃣ 순환 vs 반복

어떤 패턴이 반복된다면, 그냥 흔히 쓰는 반복문을 적용하면 되지 않나라는 의문이 들 것이다.

우리가 어떤 문제를 다루냐에 따라 순환이 효율적일 수 있고, 반복이 효율적일 수 있는데,
아래의 표에서 각 알고리즘의 특징을 알 수 있다.

Item	순환(Recursion)	반복(Iteration)
Basic	함수 호출(Function Call)	반복(Loop)
Format	종료 조건(Termination Condition) 함수 호출(Function Call)	초기화(Initialization) 제어 조건(Control Condition) 구문(Statements)
Infinite Repetition	System Crash	Infinite Loop
Stack	Yes	No
Overhead	Stack Frame	No
Speed	Slow	Fast
Code Size	Reduced	Make Longer

순환 알고리즘의 경우 반복되는 패턴을 함수 호출을 통해 처리하는데,
호출 과정에서 발생되는 Overhead로 인해 처리 속도가 상대적으로 느리다는 단점이 있다.
단 처리 과정에 대한 Code를 보다 효율적으로 작성할 수 있다는 이점이 있다.

반복 알고리즘에서는 반복되는 패턴을 Loop(for, while)를 통해 처리한다.
이는 순환 알고리즘에서처럼 함수로 인한 Overhead가 없어 수행 속도가 빠르지만
비교적 복잡한 문제를 다루기엔 Code가 길어져 어렵다는 단점이 있다.

순환 알고리즘 적용 사례

이론으로 순환 알고리즘을 이해하기는 쉽지 않다.
아래의 다양한 사례에서의 Code를 통해 순환이 어떤식으로 구현되고 활용되는지 살펴보자.

1️⃣ 팩토리얼

먼저 팩토리얼 문제를 수식으로 정의해보면 다음과 같다.
자연수 n이 주어졌을 때, n부터 1까지의 숫자를 모두 곱하는 것을 팩토리얼이라고 말한다.

팩토리얼에서는 1을 제외한 모든 수에서 $n \cdot (n-1)!$ 이라는 패턴을 가지고 있고,
이를 순환 또는 반복 알고리즘을 통해 처리할 수 있다.

순환 알고리즘

이를 순환 알고리즘으로 풀이하면, n=1 외의 조건에서는 n·(n-1)! 패턴을 함수 호출하여 해결한다.

int factorial(int n) {
    if (n <= 1)  return 1; // 종료 조건
    else return n * factorial(n - 1);
}

반복 알고리즘

반복 알고리즘에서는 1부터 n까지 반복문을 통해 곱셈 연산을 수행한다.

int factorial(int n) {
    int result = 1;
    for (int i = 1; i <= n; i++) {result *= i;}
    return result;
}

2️⃣ 피보나치 수열

피보나치 수열을 수식으로 표현하면 아래와 같고,
0과 1을 제외한 나머지 수에서는 이전 2개 항을 더한 값을 반환하는 것을 의미한다.

순환 알고리즘

위의 수식을 기준으로 종료 조건은 n=0 또는 n=1 인 경우이며, n>1인 경우에는 함수 호출을 통해 계산할 수 있다.

int fibonacci(int n) {
    if (n == 0)  // 종료 조건
        return 0;
    else if (n == 1)
        return 1;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

그런데 위와 같은 방식에서는 중복 계산이 많이 일어난다는 단점이 있다.
아래 그림은 n=6인 경우, 함수 호출이 일어나는 순서인데 fib(3)의 경우 같은 값을 계산하는 함수임에도 불구하고 3번이나 호출되는 것을 볼 수 있고, fib(2), fib(1) ... n이 작아질수록 중복 호출 횟수가 더 많아지는 것을 알 수 있다.

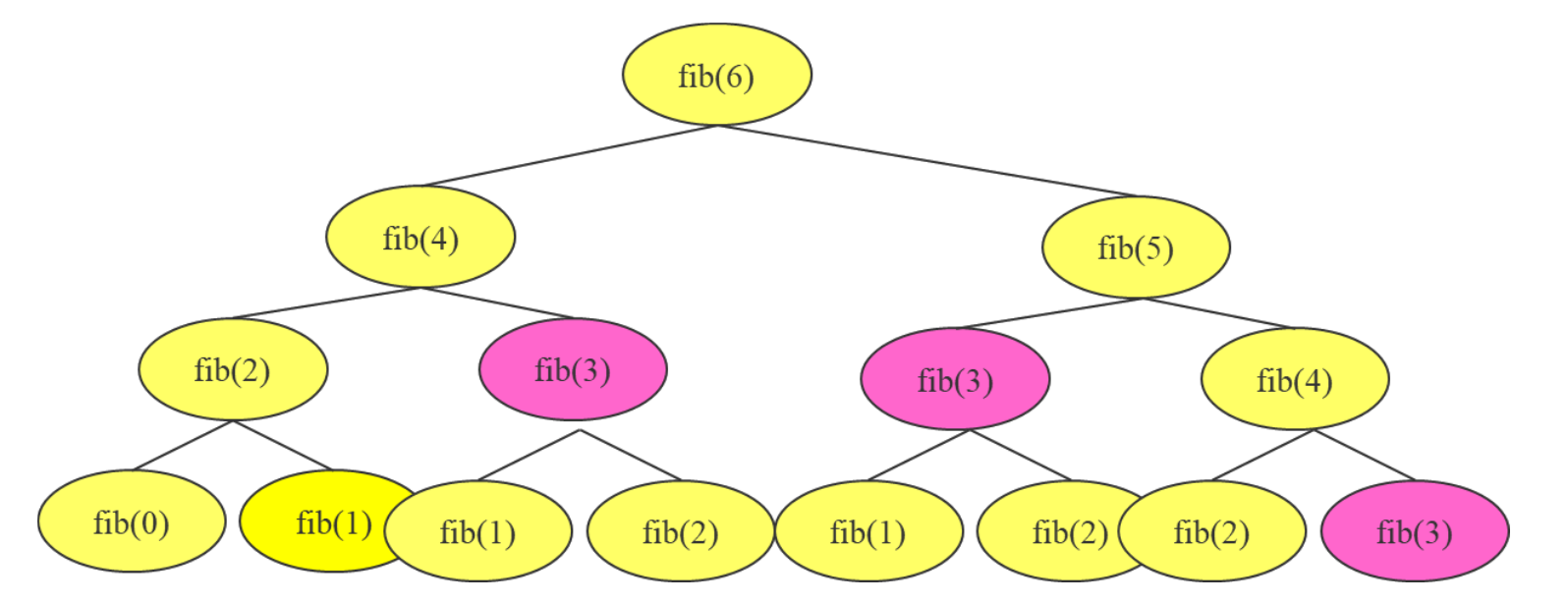
이런 중복 호출 문제를 해결하기 위해 1번 계산한 값은 변수에 저장하여 이후에 활용하는 메모이제이션을 사용할 수 있으며, 아래와 같이 이미 계산된 값이면 함수 호출을 하지 않고 저장된 값을 활용할 수 있다.

unordered_map<int, int> memo;

int fibonacci_memoization(int n) {
    if (memo.find(n) != memo.end())  // 이미 계산된 값 반환
        return memo[n];
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    memo[n] = fibonacci_memoization(n - 1) + fibonacci_memoization(n - 2);
    return memo[n];
}

반복 알고리즘

반복 알고리즘의 경우, a와 b에 이전 2개 항의 값을 계속 저장해가며 n번째 수열 값을 계산하는 방식이다.

int fibonacci(int n) {
    int a = 0, b = 1, temp;
    for (int i = 0; i < n; i++) {
        temp = a + b;
        a = b;
        b = temp;
    }
    return a;
}

3️⃣ 이진 검색

이진 검색은 크기 순으로 정렬된 데이터에서 특정 값을 검색하기 위한 효율적인 방법이다.
아래의 그림과 같이 데이터가 정렬되어 있다면, 데이터를 2개로 나누어가면서 원하는 값을 찾아낼 수 있다.

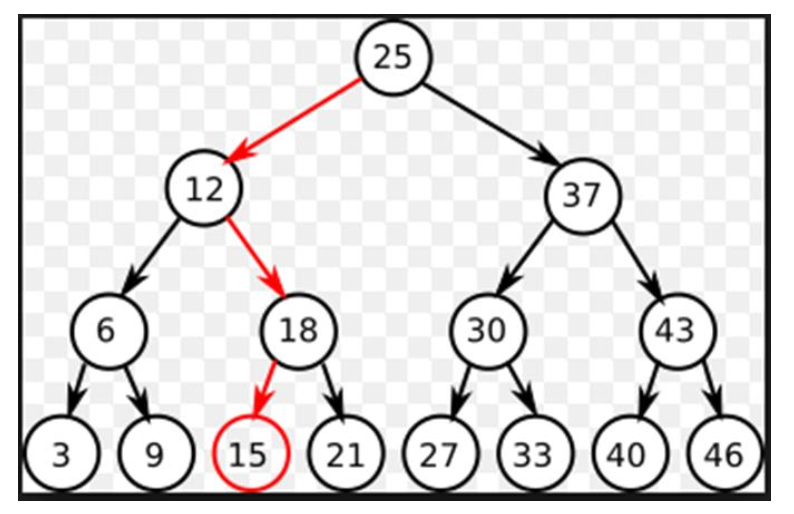
이를 각각 순환, 반복 알고리즘으로 구현한 코드는 다음과 같다.

순환 알고리즘

int binary_search(int arr[], int left, int right, int key) {
    if (left > right)  // 종료 조건: 검색 실패
        return -1;

    int mid = left + (right - left) / 2;

    if (arr[mid] == key)  // 검색 성공
        return mid;
    else if (arr[mid] > key)  // 왼쪽 부분 검색
        return binary_search(arr, left, mid - 1, key);
    else  // 오른쪽 부분 검색
        return binary_search(arr, mid + 1, right, key);
}

반복 알고리즘

int binary_search(int arr[], int n, int key) {
    int left = 0, right = n - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (arr[mid] == key)  // 검색 성공
            return mid;
        else if (arr[mid] > key)  // 왼쪽 부분 검색
            right = mid - 1;
        else  // 오른쪽 부분 검색
            left = mid + 1;
    }

    return -1;  // 검색 실패
}

순환 알고리즘 성능 분석

각각의 알고리즘에서의 성능(시간 복잡도)를 확인해보자.

1️⃣ 팩토리얼

먼저 팩토리얼의 경우 순환/반복 알고리즘의 시간 복잡도는 동일하다.
빅오표기법으로는 $\text{O(n)}$으로 표기하는 것이 맞고, 순환 알고리즘의 경우에는 함수 호출로 인한 오버헤드가 존재하기 때문에 아래 표에서는 $\alpha$를 추가해준 것이라고 보면 된다.

알고리즘 유형	시간 복잡도	비고
순환	$\text{O(n)} + \alpha$	함수 호출 (n)번 실행
반복	$\text{O(n)}$	반복문 (n)번 실행

팩토리얼의 경우에 순환 알고리즘을 사용하는 것은 적합하다라고 말할 수 있다.

2️⃣ 피보나치 수열

피보나치 수열의 경우 앞서 언급했듯이 단순 순환 알고리즘을 적용하면 중복 함수 호출이 발생하고,
이로 인해 시간 복잡도가 순환 $\text{O(2}^\text{n})$ vs 반복 $\text{O(n)}$과 같이 차이가 발생한다.

알고리즘 유형	시간 복잡도	비고
순환	$\text{O(2}^\text{n})$	중복 함수 호출로 인한 지수적 증가
반복	$\text{O(n)}$	반복문 (n)번 실행
메모이제이션	$\text{O(n)}$	중복 호출을 제거하여 선형 시간 소요

이를 보완하기 위해 순환 알고리즘에 메모이제이션을 적용한 경우에는 반복 알고리즘과 동일한 시간 복잡도를 가지는 것을 알 수 있다.
따라서 피보나치 수열의 경우 순환 알고리즘을 사용하는 것은 적합하지 않다라고 말할 수 있다.

3️⃣ 이진 검색

이진 검색의 경우도 마찬가지로 순환/반복 알고리즘 모두 $\text{O(log n)}$을 가지마ㅕ,
순환 알고리즘을 사용하는 것은 적합하다라고 말할 수 있다.

알고리즘 유형	시간 복잡도	비고
순환	$\text{O(log n)}$	배열을 절반으로 나누어 검색
반복	$\text{O(log n)}$	배열을 절반으로 나누어 검색