Propagation Kinetics

chain 중합은 chain의 active center에 monomer들이 붙어나가면서 chain이 성장하게 된다. chain 중합의 3단계 중 propagation은 수백, 수천 개의 monomer 분자가 연속적으로 추가되어 $M_1 \bullet$이 성장하는 것으로 구성된다. monomer가 추가될 때마다 moonmer 단위가 하나 더 크다는 점을 제외하면 이전과 동일한 새로운 radical을 생성하며 이때 아래와 같이 표현된다.

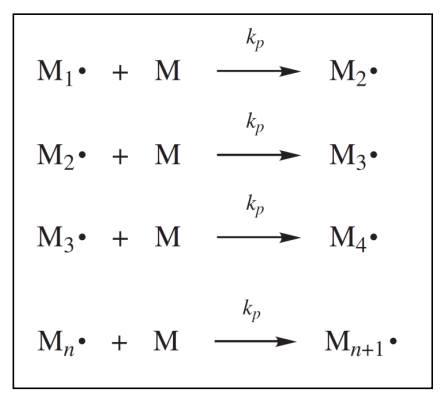
이 propatation step에서는 initiation에서 생성된 각각의 초기 라디칼 화학종에 대하여 많은 수의 monomer가 위와 같이 추가되면서 polymer로 변환된다. propagation의 속도 상수는 $k_p$로 표기하며 propagation step에서 monomer가 추가되는 모든 반응은 같은 $k_p$를 갖는 반응이라고 가정한다.

그렇다면 중합 전반에 대한 반응 속도 식을 세우면 어떻게 될까? 우선 $k_i$와 $k_p$가 라디칼의 크기에 무관한 값이라는 가정하에, monomer 분자가 소모되는(사라지는) 속도가 곧 중합 속도(rate of polymerization)이 됨을 알 수 있다. 그렇기에 다음과 같이 표기할 수 있다.

여기서 분자량이 큰 polymer가 되는 중합 반응은 initiation에서 반응하는 monomer 수보다 propagation에서 반응하는 monomer의 수가 훨씬 많다. 그렇기에 $R_p \ll R_i$이므로 다음과 같이 다시 쓸 수 있다.

그럼 이제 $R_p$는 어떻게 쓸 수 있는지 알아보자. propagation의 속도는 중합 속도와 동일하다고 하였으므로, 각 propagation step의 합으로 나타낼 수 있다.

여기서 $[M], [M\bullet]$은 각각 monomer 농도와 모든 chain radical species의 전체 농도가 된다.

Termination Kinetics

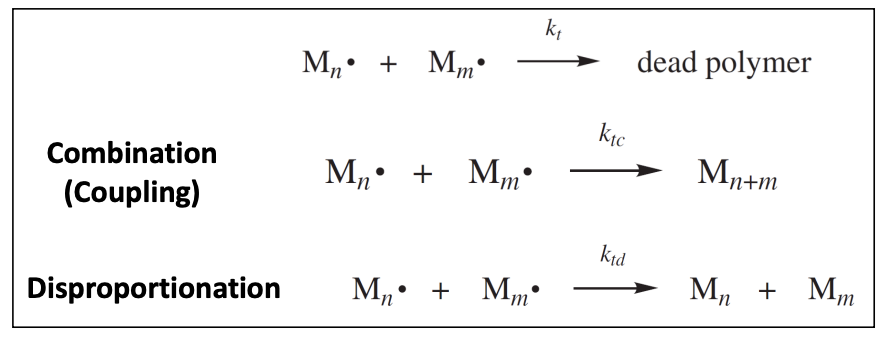
앞에서 termination step에 대해 배울 때, 위와 같이 3가지 경우의 식으로 나타낼 수 있었다. combination에 의해 라디칼 chain의 성장이 종료되는 반응 식의 속도 상수를 $k_{tc}$, disproportionation에 의한 반응 식의 속도 상수를 $k_{td}$라고 쓰면 결국 termination의 속도는 다음과 같이 쓸 수 있다.

Steady-State Assumption(Approximation)

위에서 $[M\bullet]$은 모든 chain radical species의 전체 농도라고 하였는데 이는 반응 전반에서 매우 빠르게 반응에 참여하고 초기 개시제의 농도도 매우 낮아, 아주 작은 값이므로 측정하기 힘들다. 그렇기 위해 우리는 $[M\bullet]$을 다른 변수로 치환해줄 필요가 있다. 이때 필요한 것이 Steady-State Assumption(SSA)이다. 라디칼 농도값은 초기에 증가하지만, 일정 값에 도달하게 되면 더 이상 증가하지 않는다. 즉, 상수값이 된다는 것이고 라디칼 농도의 변화 속도는 0에 수렴한다는 의미이다. 이때의 값을 steady-state value라고 하며, 개시 속도 $R_i$와 정지 속도 $R_t$가 같다는 의미가 된다.

위 식을 $[M\bullet]$에 대해 정리하면,

위 식을 $R_p$에 대입해주면, 다음과 같이 다시 쓸 수 있을 것이다.

이 결론으로 알 수 있는 것은 중합 속도는 monomer의 농도에 비례하고 개시 속도와 개시제의 농도의 제곱근에 비례한다는 것이다. 즉, 개시 속도를 2배로 증가시켜도 중합 속도는 2배 증가되지 못하고 $\sqrt{2}$배만큼 빨라진다.