[고분자 화학] 3-6a Effect of Chain Transfer

jmt·2024년 6월 23일

고분자화학

목록 보기

18/27

Chain Transfer Reaction

많은 중합 시스템에서 고분자의 molecular weight는 예상한 것보다 낮게 나오는데 그 이유는 라디칼 체인 중합에서 initiation / propagation / termination 3단계의 반응만 일어나지 않고 chain transfer와 같은 예상치 못한 추가적인 반응이 존재하기 때문이다. chain transfer의 효과는 성장하는 체인이 계에 존재하는 다른 화합물로부터 수소나 다른 원자 또는 다른 종의 이동에 의해 정상적인 termination보다 더 빠르게 성장이 멈추기 때문에 일어난다. 이러한 라디칼의 위치가 바뀌는 반응을 chain transfer reaction이라고 한다. 다음과 같은 도식도를 보자.

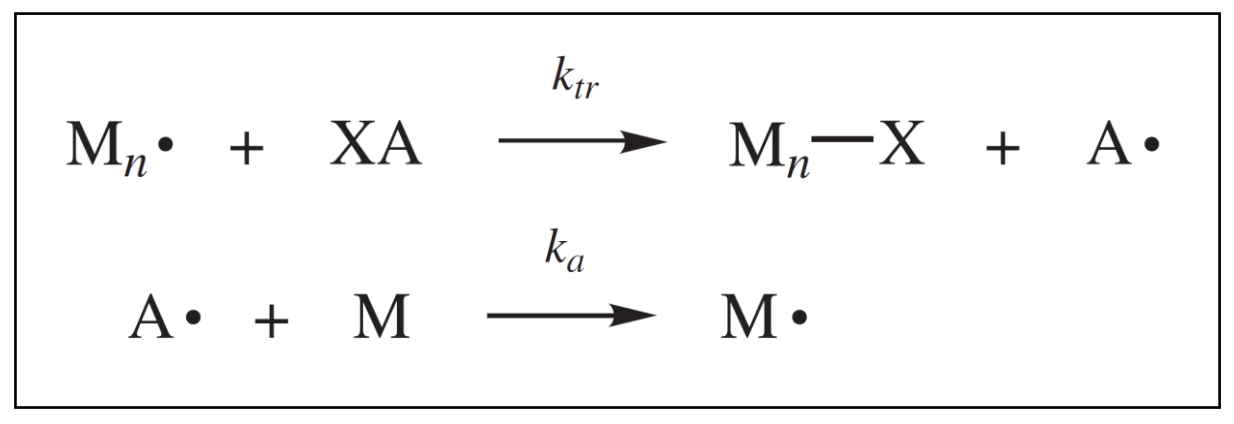
여기서 $XA$ 는 monomer, initiator, solvent, chain transfer agent 혹은 그 외의 물질이 될 수 있다. $X$ 는 전이(transfer)가 일어나는 원자나 화학종이 된다. $M_n \bullet$ 과 같이 성장하는 chain이 $XA$ 와 반응하게 되면 성장 중인 chain의 라디칼이 제거되어 $A\bullet$ 으로 이동하게 된다. 이 반응 생성물인 $M_n-X$ 는 active center(radical)이 사라졌기에 여기서 더 이상 성장하지 못하고 반응이 종료된다. 그리고 생성된 $A\bullet$ 은 monomer를 공격하여 $M\bullet$ 을 생성하여 다시 새로운 chain이 성장하게 된다. 이러한 반응에 따라 예상했던 것보다 더 낮은 molecular weight의 고분자가 생성되는 것이다.

Rate of Chain Transfer Reaction

이번엔 chain transfer 반응의 속도를 알아보자. 우선 첫번째 반응식에 따라 다음과 같이 쓸 수 있다.

R_{tr} = k_{tr}[M\bullet][XA]

여기서 $k_{tr}$ 은 chain transfer 반응의 속도 상수가 된다. 그리고 chain transfer의 결과로 새로운 라디칼 $A\bullet$ 이 생산되고 이는 다시 중합 반응을 시작하게 한다. 이것이 위 chain transfer reaction의 두번째 식이 되고 이 반응의 속도 상수를 $k_a$ 로 표시한다. 위에서 이야기했듯이 chain transfer는 결국 propagating 고분자 체인의 크기를 감소시키게 되고 이는 $R_p$ 나 $\bar{X}_n$ 에도 영향을 주게 될 것이다. 다만 아래와 같은 4가지 경우에 따라 chain transfer effect가 중합 속도와 수평균 중합도에 어떤 영향을 끼치는 지는 달라진다.

위 표에서 $k_a$ 와 $k_{tr}$ 의 대소관계에 따라 4가지로 경우를 나누었다. 우선 case 1, 2와 case 3, 4를 보면 새로운 라디칼 $A\bullet$ 에 의해 중합 반응이 다시 개시되는 속도가 기존의 중합 반응의 propagation 속도 $k_p$ 와 비슷한 지 혹은 $k_p$ 보다 느린지에 따라 분류하였다. 그리고 case 1과 2 그리고 case 3과 4를 각각 $k_p$ 와 $k_{tr}$ 의 대소 관게에 따라 분류하였다. case 1과 3은 chain transfer reaction의 속도보다 기존의 성장 중인 chain이 propagation하는 속도가 훨씬 큰 경우가 된다. case 2와 4는 이와 반대로 chain transfer reaction의 속도가 훨씬 큰 경우가 된다. 차례로 case1부터 어떻게 될지 예상해보자.

Case 1

우선 case1의 경우에는 $k_p \gg k_{tr}$ 이므로 chain transfer가 비교적 많이 일어나지 않을 것이다. 또한 $k_p \approx k_a$ 이므로 중합 속도( $R_p$ )에는 큰 영향을 주지 않는다. 즉 이 경우는 일반적인 chain transfer가 가끔 일어나는 경우로 수평균 중합도( $\bar{X}_n$ )의 값은 예상치보다 약간 감소하게 될 것이다.

Case 2

case 2의 경우에는 case 1과 다른 점이 $k_p \ll k_{tr}$ 이다. 즉, chain transfer reaction의 속도가 빠르기에 훨씬 빈번하게 chain transfer가 발생하게 된다. 이는 성장 중인 chain이 propagation step을 통해 높은 molecular weight의 고분자가 되지 못하고 비교적 연결되는 monomer의 수가 낮기에 낮은 molecular weight의 화학종이 되게끔 할 것이다. 이러한 형상을 Telomerization이라고 부른다. 우리가 step 중합에서 monomer, dimer, trimer, ... 의 화학종이 계속 진행되면서 어느정도 monomer가 중합된 chian을 oligomer라고 부르는데, 이 oligomer의 수평균 중합도는 $\bar{X}_n > 10$ 정도가 된다. 그런데 telomer는 수평균 중합도가 $\bar{X}_n = 1 \sim 5$ 정도로 고분자라고는 정의할 수 없다. 이렇게 telomer를 형성하는 과정을 telomerization이라 한다. 그러므로 중합 속도( $R_p$ )에는 영향을 주지 못하지만, telomerization에 의해 전체 반응의 수평균 중합도는 매우 크게 감소하게 될 것이다.

Case 3

case 3은 case 1과 비슷하게 chain transfer가 빈번하게 일어나지는 않지만, $k_a < k_p$ 이므로 새롭게 형성된 라디칼 $A\bullet$ 에 의한 반응보다 기존의 반응속도가 빠르다는 의미가 된다. 즉, $A\bullet$ 이 반응하여 이루어지는 $M\bullet$ 의 성장이 지연(retardation)된다. 그러므로 전체 중합 속도( $R_p$ )는 감소하게 되고 chain transfer에 의해 예상치보다 수평균 중합도( $\bar{X}_n$ )도 감소하게 될 것이다.

Case 4

case 4는 case 2처럼 chain transfer가 매우 빈번하게 발생함과 동시에 case 3처럼 $k_a < k_p$ 이므로 chain transfer에 의해 서로 성장하는 chain $M\bullet$ 의 성장속도가 매우 느리다. 이는 Degradative Chain Transfer를 유발하는데, 그 결과로 중합 속도( $R_p$ )와 수평균 중합도( $\bar{X}_n$ ) 두 값 모두 매우 감소한다.

Chain Transfer Kinetics

이제 chain transfer의 영향을 알아보았으니, 라디칼 체인 중합에서 Initiation, Propagation, Termination 3단계외에도 chain transfer를 고려하여 수평균 중합도 $\bar{X}_n$ 을 새로 정의해보자. 우선 중합 system에서 일어날 수 있는 모든 반응 중 chain의 성장이 종료되는 반응을 모두 써보면 기존의 2개에 chain transfer reaction 3개가 추가될 것이다.

combination
disproportionation
chain transfer to monomer
chain transfer to initiator
chain transfer to compound S(= chain transfer agent)

이 의미는 기존의 $\bar{X}_n$ 의 정의가 성립하지 않는다는 소리이다.

\bar{X}_n \neq \frac{2k_t v}{(k_{tc} + 2k_{td})}

Mayo Equation

우선 위에서 언급한대로 chain transfer reaction을 termination에 추가하게 되면 rate of termination, $R_t$ 의 값을 다음과 같이 새로 정의할 수 있다.

R_t = k_{tc}[M\bullet]^2 + 2k_{td}[M\bullet]^2 + k_{tr}[XA][M\bullet]

그리고 수평균 중합도 정의에서 SSA에 의해 $R_i = R_t$ 임을 고려하면,

\begin{aligned} \bar{X}_n &= \frac{R_p}{R_t} = \frac{k_p[M][M\bullet]}{k_{tc}[M\bullet]^2 + 2k_{td}[M\bullet]^2 + k_{tr}[XA][M\bullet]}\\ &= \frac{k_p[M]}{k_{tc}[M\bullet] + 2k_{td}[M\bullet] + k_{tr}[XA]}\\ &= \frac{k_p[M]}{k_{tc}[M\bullet] + 2k_{td}[M\bullet] + k_{tr, M}[M] + k_{tr, I}[I] + k_{tr, S}[S]}\\ \end{aligned}

chain transfer reaction에서 monomer, $[M]$ 로 라디칼이 이동하는 경우(즉, [XA]가 monomer인 경우)와 initiator, $[I]$ 로 라디칼이 이동하는 경우, chain transfer agent $[S]$ 로 라디칼이 이동하는 경우를 각각 고려하면 $k_{tr}$ 에 대한 항을 마지막 식처럼 3개의 항으로 나눠 쓸 수 있다. 그리고 이때의 속도 상수 값은 각각 $k_{tr, M}, k_{tr, I}, k_{tr, S}$ 로 모두 다른 값임에 유의하자. 마지막 식에서 $[M\bullet]$ 를 $R_p$ 의 정의로 부터 유도하여 대입해주자.

R_p = k_p[M][M\bullet] \rightarrow [M\bullet] = \frac{R_p}{k_p[M]}

그리고 분자, 분모에 $k_p[M]$ 을 곱해주면,

\begin{aligned} \bar{X}_n &= \frac{k_p^2[M]^2}{k_{tc}R_p + 2k_{td}R_p + k_{tr, M}k_p[M]^2 + k_{tr, I}k_p[I][M] + k_{tr, S}k_p[S][M]} \end{aligned}

위 식에서 역수를 취해주면,

\begin{aligned} \frac{1}{\bar{X}_n} &= \frac{k_{tc}R_p + 2k_{td}R_p + k_{tr, M}k_p[M]^2 + k_{tr, I}k_p[I][M] + k_{tr, S}k_p[S][M]}{k_p^2[M]^2}\\ &= \frac{R_p}{k_p^2[M]^2}\left(k_{tc} + 2k_{td} \right) + \frac{k_{tr, M}}{k_p} + \frac{k_{tr, I}[I]}{k_p[M]} + \frac{k_{tr, S}[S]}{k_p[M]}\\ &= \frac{R_pk_t}{k_p^2[M]^2} + \frac{k_{tr, M}}{k_p} + \frac{k_{tr, I}[I]}{k_p[M]} + \frac{k_{tr, S}[S]}{k_p[M]} \end{aligned}

마지막 식에서 $R_p^2 = k_p^2 [M]^2 [M\bullet]^2$ 임을 이용해보자. 우선 양변을 적절히 나누면,

\frac{1}{k_p^2[M]^2} = \frac{[M\bullet]^2}{R_p^2}

이다. 여기서 SSA에 의해 $[M\bullet] = \left(\frac{R_i}{2k_t} \right)^{1/2}$ 이므로 이 값을 위 식에 대입해주면,

\frac{1}{k_p^2[M]^2} = \frac{R_i}{2k_tR_p^2}

이다. 이제 이 값을 이용하여 수평균 중합도 식에 대입해주면,

\begin{aligned} \frac{1}{\bar{X}_n} &= \frac{R_iR_pk_t}{2k_tR_p^2} + \frac{k_{tr, M}}{k_p} + \frac{k_{tr, I}[I]}{k_p[M]} + \frac{k_{tr, S}[S]}{k_p[M]}\\ &= \frac{R_i}{2R_p} + \frac{k_{tr, M}}{k_p} + \frac{k_{tr, I}[I]}{k_p[M]} + \frac{k_{tr, S}[S]}{k_p[M]} \end{aligned}

가 된다. 이렇게 수평균 중합도 $\bar{X}_n$ 에 chain transfer reaction을 고려한 식을 Mayo Equation이라 부른다. 여기서 좀 더 깔끔하게 식을 표현하기 위해 아래와 같은 속도 상수를 정의하자.

C_M = \frac{k_{tr, M}}{k_p};\quad C_I = \frac{k_{tr, I}}{k_p};\quad C_S = \frac{k_{tr, S}}{k_p}

이 chain transfer constants를 이용하여 Mayo Equation을 다시 쓰면,

\begin{aligned} \frac{1}{\bar{X}_n} &= \frac{R_i}{2R_p} + C_M + C_I\frac{[I]}{[M]} + C_S\frac{[S]}{[M]}\\ &= \frac{R_pk_t}{k_p^2[M]^2} + C_M + C_I\frac{[I]}{[M]} + C_S\frac{[S]}{[M]}\\ &= \frac{R_pk_t}{k_p^2[M]^2} + C_M + C_I\frac{k_tR_p^2}{k_p^2fk_d[M]^3} + C_S\frac{[S]}{[M]} \end{aligned}

이 Mayo equation은 다양한 chain transfer reaction의 효과가 수평균 중합도 $\bar{X}_n$ 에 어떤 정량적인 영향을 주는지를 알려준다. 그리고 반응 매개변수 $R_i, C_M, C_I, C_S, R_p$ 를 통제함으로 원하는 $\bar{X}_n$ 을 구할 수 있게 해준다.