Introduction

중합 반응을 어떻게 진행할지를 결정하는데 있어 온도가 중합 반응의 속도와 수평균 중합도에 미치는 영향이 가장 중요하다. 일반적으로 대부분의 step 중합은 온도가 증가함에 따라 중합 속도가 증가하고 molecular weight($\approx$ 수평균 중합도)도 증가하게 된다. step 중합은 functional group이 반응하면서 다양한 species들끼리의 반응으로 진행되기 때문에 side reaction이 일어날 확률이 직기 때문이다. 반면 radical chain 중합의 경우에는 온도가 증가함에 따라 중합 속도는 증가하지만 molecular weight는 낮아지는 것을 확인할 수 있다. 이는 아래의 그래프에서 $x$축을 $T^{-1}$로 두고 $y$축을 $R_p$로 plot했을 때를 보면 확인할 수 있다.

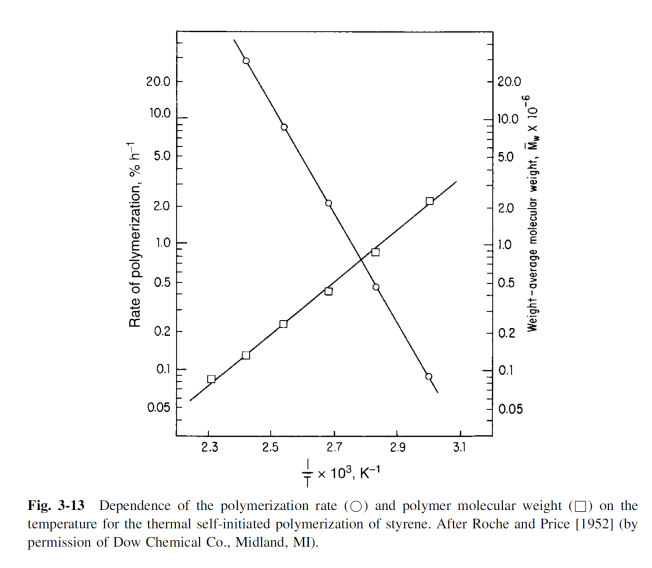
그 이유는 chain 중합, 그 중에서도 radical chain 중합의 경우에는 반응성이 높은 radical(radical이 아니여도 reactive species)에 의한 side reaction이 일어날 확률이 높기 때문이다. 그렇기에 온도가 증가하면 중합 속도가 증가하면서 side reaction이 일어날 확률도 같이 높아진다. 중합 속도 $R_p$와 수평균 중합도 $\bar{X}_n$은 $k_d, k_p, k_t$ 3개의 반응 속도 상수에 의존하는 값이므로 온도의 정량적인 영향을 유도하는 것은 매우 복잡하다. 그렇기에 chain 중합에서의 3단계, initiation, propagation, termination의 속도 상수를 Arrhenius 형태의 식을 사용하여 표현한다.

Arrhenius-type Relationship

Arrhenius-type relationship은 온도와 활성화 에너지(activation energy)를 통해 반응 속도 상수를 표현하게끔 해준다. Arrhenius 식은 다음과 같다.

여기서 당연히 $k$는 속도 상수이고, $A$는 충돌 빈도를 나타내는 상수이고, $E$가 Arrhenius 활성화 에너지가 된다. $R$과 $T$는 각각 기체 상수와 온도를 나타낸다. 이 식을 이용하여 $k_d, k_p, k_t$를 표현하면 다음과 같다.

반응 속도를 계산하기 위해서는 $k_d, k_p, k_t$를 모두 구해야하고 이때 온도가 미치는 영향을 구하기 위해서는 더 복잡해진다. 하지만 Arrhenius 식을 이용하면 $R_p$는 다음과 같이 정리된다.

이때 $E_R$을 중합 속도를 계산하기 위한 전반적인 activation energy로 정의하자. 여기서 주의할 점은 중합 반응에 전체적으로 필요한 activation energy가 아닌 $E_d, E_p, E_t$를 묶어 표현하기 위한 activation enenrgy이다. 그러면 $E_R$을 다음과 같이 표현할 수 있다.

위 값을 그대로 $R_p$에 대입하면,

Rate of Polymerization

이제 $R_p$의 온도에 대한 영향을 알아보기 위해서 양변에 $\ln$을 취하면,

위 식에서 $y$를 $R_p$, $x$를 $T^{-1}$로 두고 선형회귀/외삽을 하면 기울기와 $y$절편을 구할 수 있게 되고 이 값을 통해 $E_R$과 $A_p\left(\frac{A_p}{A_t} \right)^{1/2}$를 구할 수 있다. 또한 온도가 증가함에 따라 중합 속도, $R_p$가 증가하는 이유도 밝힐 수 있다. 위 식을 온도에 대해 편미분하면,

이므로 만약 $E_R > 0$이라면, 온도에 대해 편미분한 값이 항상 양수이므로 $T$가 증가함에 따라 $R_p$도 증가하는 관계임을 알 수 있다. 다만 여기서 $E_R > 0$임을 어떻게 알 수 있을까? 우선 $E_d$는 개시제의 thermal decomposition에 의한 activation energy이다. 이 값은 대부분의 initiator에 대해 $110 < E_d < 160$이고, $E_p$은 propagation step에 필요한 activation energy로 $15 < E_p < 40$이다. 마지막으로 $E_t$는 termination step에 필요한 activation energy로 $30 < E_t < 80$의 값을 갖는다. 그렇기에 중합 속도를 계산할 때 $E_R > 0$이므로 온도가 증가함에 따라 중합 속도도 증가한다고 결론 지을 수 있다.

Degree of Polymerization

수평균 중합도와 온도의 관계는 어떻게 될까? 우선 위에서 온도가 증가함에 따라 side reaction이 일어날 확률이 증가하여 molecular weight가 감소한다고 하였으므로 $\bar{X}_n$과 온도는 반비례 관계가 될 것임을 예상할 수 있다. 이번에도 Arrhenius 식을 활용하여 증명해보자. 우선 수평균 중합도의 정의에 따라 아래와 같이 정의할 수 있다.

여기서 SSA에 의해 다음이 성립한다.

이 식을 $[M\bullet]$에 대해 정리하면,

이므로 이 식을 수평균 중합도 식에 대입하고 마찬가지로 Arrhenius 식으로 표현하면,

중합 속도에서 $E_R$을 정의했던 것과 동일한 방식으로 $E_R$을 정의하면 수평균 중합도를 계산할 때 $E_R$은 다음과 같다.

그럼 수평균 중합도 $\bar{X}_n$은 다음과 같다.

온도가 증가함에 따라 어떻게 변화하는 지 알아보기 위해 양번에 $\ln$을 취한다.

$T$에 대해 편미분하면,

수평균 중합도를 계산할 때 정의한 $E_R$은 $E_R < 0$이므로 온도가 증가함에 따라 $\bar{X}_n$은 감소하는 관계를 갖는다. 즉, 라디칼 chain 중합에서 온도가 증가함에 따라 수평균 중합도는 감소하기에 molecular weight가 감소한다고 결론내릴 수 있다.

Thermodynamics of Polymerization

열역학에서 반응이 자발적인지 비자발적인지 알아보기 위해서는 $\Delta G$을 알아보면 된다. $\Delta G <0$이면 자발적이다. $\Delta G = \Delta H -T \Delta S$이므로 enthalpy의 변화와 entropy의 변화를 각각 알아보자. 우선 라디칼 chian 중합은 라디칼이 vinyl monomer의 $\pi$ 결합을 공격하여 $\sigma$ 결합으로 바뀌면서 고분자에 monomer가 추가된다. 이때 상당한 열이 발생하기 때문에 발열 반응(exothermic)이고, $\Delta H < 0$이 된다. entropy의 변화와 같은 경우에는 무질서도로 entropy를 정의하게 되면, monomer 분자들의 높은 무질서도에서 고분자로 변하면서 하나의 정렬된 구조가 된다. 그렇기에 무질서도는 감소하게 되고 $\Delta S <0$이라 할 수 있다. 그럼 중합 반응은 enthalpy의 관점에서는 중합 반응은 자발적이지만, entropy 관점에서는 비자발적일 수 있게 된다. 하지만 중합은 자발적인 반응이 되는데 그 이유는 아래의 표를 통해 알 수 있다.

대부분의 monomer에 대해서 $-\Delta H < -\Delta S$이므로 $\Delta G < 0$이 되고 중합 반응은 자발적이다. 여기서 monomer에 따라 $\Delta H$의 차이를 보이는 이유는 vinyl기에 붙어 있는 치환체(substituent)가 다르기 때문이다.

Kinetic Feasibility

하지만 중합 반응이 열역학적 측면에서 선호된다고 하여도 속도론적 측면에서도 선호되는지 확인이 필요하다. chain 중합은 radical, cationic, anionic initiation이 충분히 빠른 속도로 일어날 수 있는 지에 따라 구분된다. 이는 앞에서 radical versus ionic polymerization 에서 다루었던 부분이다. 아래의 표는 속도론적 관점에서 개시 반응이 충분히 빠른 속도로 일어날 수 있는지에 따라 가능한 chain 중합을 나타낸 것이다.

Effect of Monomer Structure

$\Delta H$는 monomer의 종류에 따라 달라진다고 하였는데, 이는 치환기가 제각각이기 때문이다. ethylene, propene, 1-butene의 구조를 살펴보자. (이들은 $\alpha$-olefin이다.)

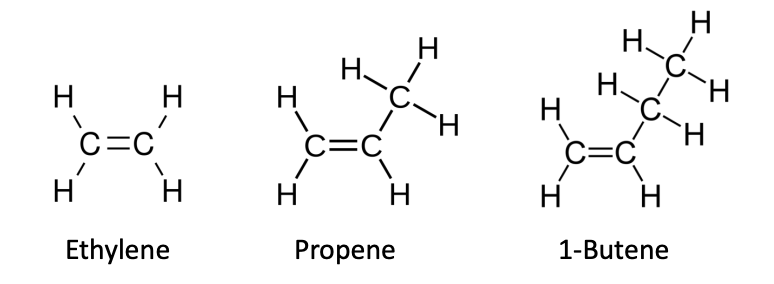
alkene의 $\pi$ bond의 에너지와 $\sigma$ bond의 에너지의 차이가 $\Delta H$의 차이와 비슷하다. 하지만 이것으로 $\Delta H$를 정의할 수는 없다.

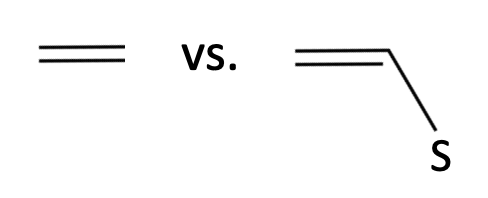
치환체($S$로 표기)가 있는 ethylene 경우에는 $\Delta H$ 값에 큰 차이를 보이기 때문이다. 이 경우의 $\Delta H$의 차이는 아래와 같은 원인들로 계산된다.

1. 공명 안정화(resonance stabilization)
2. 입체 방해(steric strain)
3. 수소 결합 혹은 쌍극자 상호작용(hydrogen bonding or dipole interaction)

Resonance Stabilization Effect

위 그림과 같은 benzene ring이나 alkene double bond, carbonyl linkage, nitrile group을 갖는 치환체에 있는 탄소-탄소 이중 결합은 공명 구조를 가질 수 있게 하여 반응물인 monomer를 안정화시킨다. 그 결과로 반응물의 enthalpy가 감소하기에 중합 반응의 $\Delta H$도 감소한다.

Steric Strain Effect

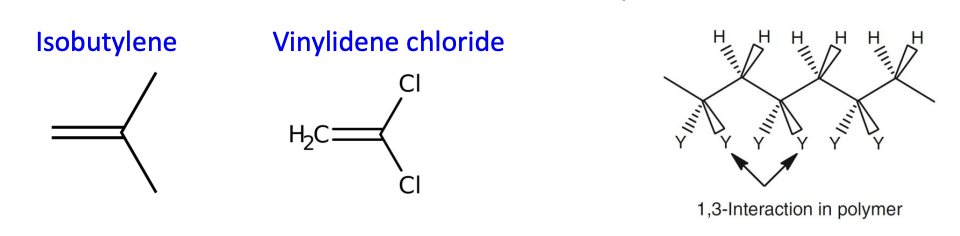
위와 같은 1,1-이중치환(distirbution)도 $\Delta H$를 감소시킨다. 그 이유는 중합 후 형성된 polymer의 구조가 불안정해지기 때문에 반응 생성물의 enthalpy가 증가한다. 그러므로 $\Delta H$는 감소하는 것이다.

Hydrogen Bonding Effect

acrylic acid나 acylamide와 같은 monomer는 monomer 간의 intermolecular force가 작용하여 수소 결합이 일어날 수 있다. 이로 인해 monomer가 안정화되기 때문에, 반응물의 enthalpy가 감소하여 $\Delta H$가 감소하게 된다.

결론적으로 $\Delta H$ 값은 monomer에 따라 넓은 범위의 값을 갖지만 $\Delta S$의 값은 monomer의 구조에 덜 민감하고 비교적 일정하게 $100 \sim 120 \text{JK}^{-1}\text{mol}^{-1}$의 범위내에 존재한다. 그러므로 $\Delta G$에 대한 entropy term, $T\Delta S$의 기여도는 작다고 볼 수 있다. 더 자세히 설명하면, 중합의 $\Delta S$는 주로 monomer의 translational entropy의 손실에 의해 일어난다. 분자의 운동 중 rotational과 vibrational entropy의 변화는 고분자의 rotational, vibrational entropy의 증가로 $\Delta S$에 큰 영향을 주지 않기 때문이다. 그러므로 monomer의 translational entropy에 의해 중합의 $\Delta S$가 계산되는데, translational entropy는 monomer의 구조에는 비교적 관계가 없다.

Polymerization of 1,2-Disubstituted Ethylenes

한 종류의 치환체를 갖는 monomer로 일어나는 중합, homopolymerization은 입체 방해에 의해 잘 일어나지 않는다. 그 이유는 propagating radical이 monomer의 구조에 의해 강한 입체 방해를 받기 때문에 monomer를 쉽게 공격할 수 없기 때문이다. 하지만 copolymerization(공중합)은 가능하다.

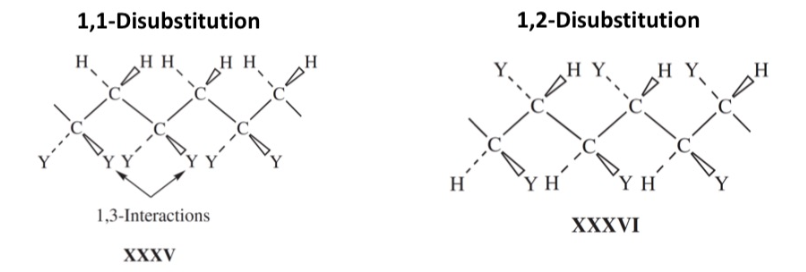
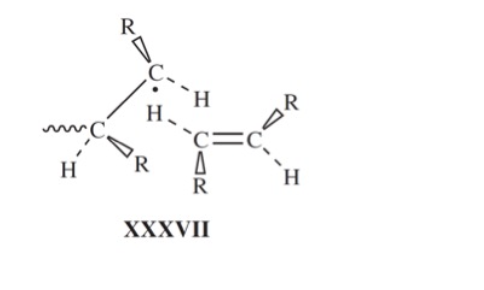
위 그림을 보면 알 수 있듯이, 1,2-disubstituted ethylene으로 중합된 고분자 $\text{XXXVI}$는 1,1-disubstituted ethylene으로 얻어진 $\text{XXXV}$보다 비교적 적은 입체 방해를 받는다는 것을 알 수 있다. $\text{XXXV}$와 $\text{XXXVI}$는 같은 수의 1,3-interactionㅇ 존재하지만, 그 분포가 다르다. 실제로 $-\Delta H$ 값을 비교해보면, 1,1-disubstituted ethylene인 isobutylene보다 1,2-disubstituted ethylene인 maleic anhydride가 $48 < 59\text{kJ}\text{mol}^{-1}$로 훨씬 중합에 유리한 값을 갖는다는 것을 확인할 수 있다. 하지만 1,2-disubstituted ethylene의 중합 반응이 자발적이지 못한 이유는 열역학적 요인에 더하여 속도론적 요인 때문이다. monomer로 propagating radical이 공격할 때 아래와 같은 구조로 인해 입체 방해를 받기 때문에 충분한 속도로 중합 반응이 일어나기 힘들다.

Polymerization-Depolymerization Equilibria

앞에서 온도가 증가함에 따라 중합 속도가 증가한다는 예측은 propagation step이 비가역적이라는 가정에 근거하였다. 만약 역반응이 가능하다면 어떻게 될까? 대부분의 중합 반응에 있어서 반응이 가역적으로 일어나는 온도가 존재한다. 이 경우 propagation step의 반응은 평형 반응으로 표현되어야 한다.

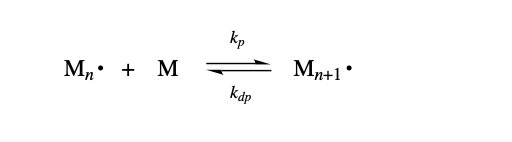
위 식에서 $k_{dp}$는 역반응 속도 상수가 되고, 이 역반응을 depolymerization, depropagation이라 한다. 중합 반응에서 온도의 전반적인 영향은 이러한 정반응과 역반응의 평형 관계에 의해 복잡해진다. 우선 온도가 증가함에 따라 $k_p$가 증가하여 중합 속도가 증가하게 된다. 하지만 점점 온도를 올릴수록 초기에는 0이였던 $k_{dp}$도 같이 증가하면서 상당한 값에 도달하게 된다. 최종적으로 특정 온도($T_c$, Ceiling Temperature)에 도달하면 propagation이 일어나는 속도와 depropagation이 일어나는 속도가 같아진다. 즉, $T_c$에서 polymer의 생성 알짜 속도는 0이 된다. 그리고 ceiling temperature, $T_c$를 monomer의 중합이 일어나는 가장 높은 온도라 정의할 수 있다. 그럼 $T_c$보다 높은 온도에서는 중합 반응의 평형이 역반응쪽으로 이동해 polymer가 다시 monomer로 돌아가는 depolymerization(해중합)이 일어난다. $T_c$에서는 중합 속도가 해중합 속도와 같아서 chain의 성장이 일어나지 않는다. 아래 그래프는 styrene의 온도에 따른 $k_p[M]$과 $k_{dp}$의 변화를 보여준다.

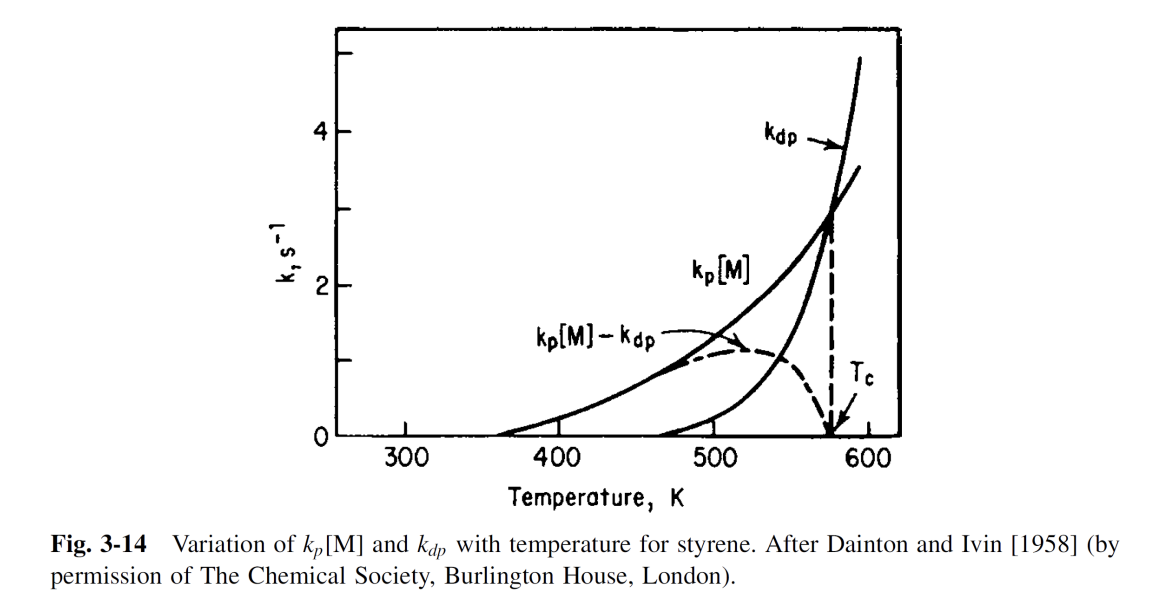
Polymerization-Depolymerization Equilibria를 분석하기 위해 아래와 같은 식을 사용할 수 있다.

$\Delta G^{\circ}$는 적절한 표준 상태에 있는 monomer와 polymer의 $\Delta G$를 의미한다. monomer의 표준 상태는 순수한 액체 상태 혹은 1M 용액으로 하는 경우가 많다. 그리고 polymer의 표준 상태는 고체 상태의 amorphous이거나 약간의 crystalline인 고분자 혹은 repeating unit의 농도가 1M인 용액을 말한다. 또한 평형 상태에서는 $\Delta G = 0, Q=K$이기 때문에, 아래와 같은 관계식을 얻을 수 있다.

그리고 평형 상수 $K$는 그 정의에 의해 $\frac{k_p}{k_{dp}}$가 되고 propagation step의 평형 반응 식에 의해 다음과 같이 쓸 수 있다.

그럼 최종적으로 $\Delta G^{circ}$의 식에서 구한 $K$ 값을 대입하고 $T$에 대해 정리하면, 다음과 같이 ceiling temperature, $T_c$를 구할 수 있고, 이때의 monomer 농도 $[M]_c$도 구할 수 있다.