Introduction

고분자의 molar mass를 구하기 위해 colligative properties를 이용해 수 평균 분자량 $M_n$을 구하였고, 입자의 크기 $d$가 파장의 크기 $\lambda$보다 작은 경우, Reighleigh scattering인 경우에 어떻게 $M_w$를 구할 수 있는지에 대해 알아보았다. 그리고 Chain Size - part 1에서는 $d > \lambda$의 경우, Mie scattering의 경우, 각도 의존성이 커지기 때문에 light scattering에 size effect를 고려하게 되었다. size effect를 고려하게 되면, Form factor $P(q)$를 통해 size가 커짐에 따라 각도 의존성을 나타내었고, 이를 Guinier plot, Zimm plot으로 나타내어 $\langle R_g^2\rangle$인 회전 반경(radius of gyration)을 구할 수도 있었다. 하지만, 여태까지 배운 light scattering은 static light scattering으로 입자가 시간에 따라 상대적인 위치가 변하지 않는 경우이다. static light scattering은 측정 시간이 길고, 비교적 복잡한 방법이기 때문에, 현대에 와서는 dynamic light scattering을 주로 사용하게 된다. 이번에는 dynamic light scattering이란 무엇인지, 그리고 dynamic light scattering(이하 DLS)에서는 어떤 물리량들을 구할 수 있는지 알아보도록 하자.

Dynamic Light Scattering

dynamic light scattering은 suspension이나 고분자 용액(solution) 내의 입자의 크기를 측정할 수 있는 방법이다. 현탁액 속에서 작은 입자들은 브라운 운동(Brownian motion)을 하기 때문에, 입자의 상대적인 거리가 시간에 따라 계속 변화하게 된다. 이러한 위치 변화가 위상 변화의 결과로 빛의 간섭현상이 시간에 따라 변화하게 되므로 산란광의 세기가 시간에 다라 변화한다. 그럼 Static Light Scattering과 다르게 시간에 따른 산란광의 세기에 noise가 상당히 많은 데이터를 얻게 된다.

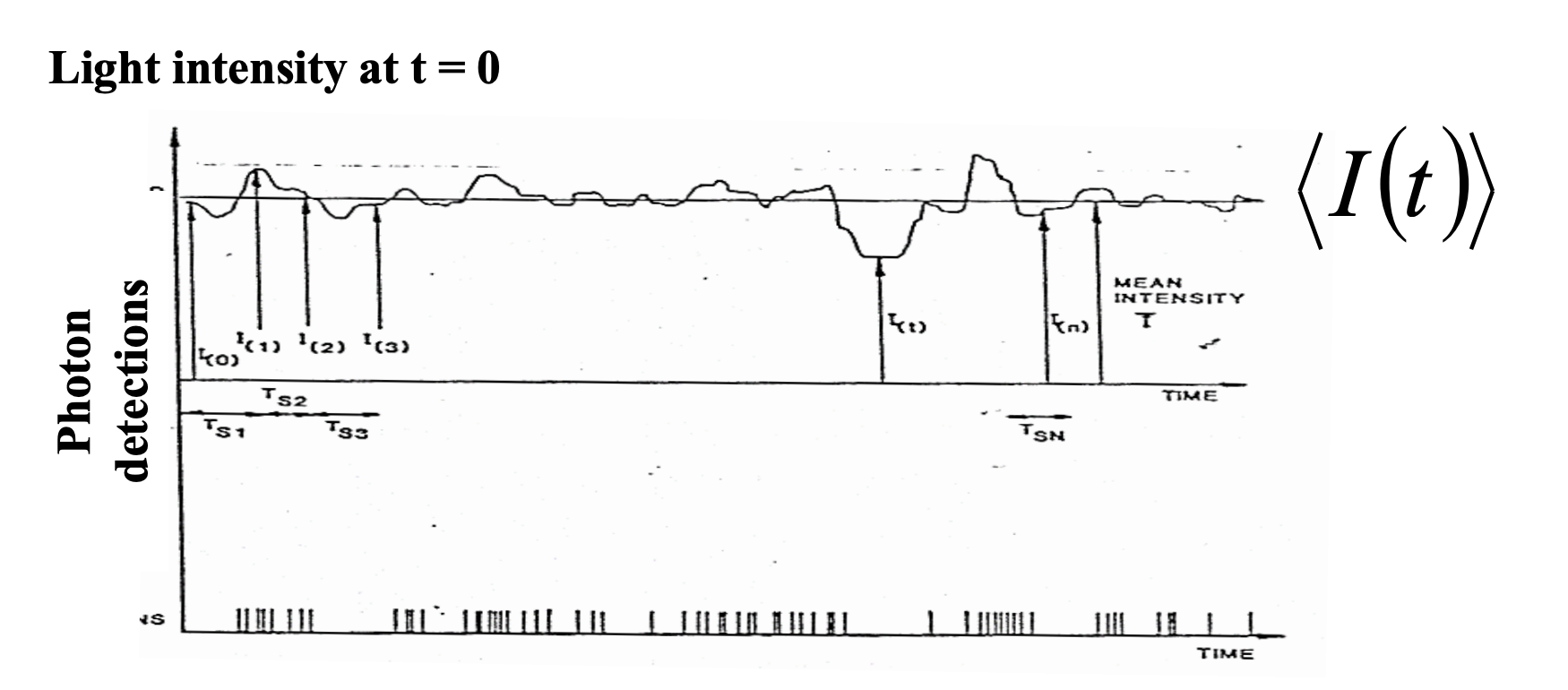
이러한 noise들은 큰 입자일수록 상대적인 위치가 천천히 변화하게 되어 시간에 대한 상관관계(correlation)이 길다고 할 수 있고, 작은 입자일수록 더 빠르게 움직여 시간에 대한 상관관계가 짧다고 할 수 있다. 그렇다면 이렇게 noise가 있는 데이터로 무엇을 해석할 수 있을까? 산란광의 세기의 시간에 따른 변화를 추적하면, 분자의 운동을 알 수 있고, 분자의 운동은 확산 계수와 관계가 있기 때문에 최종적으로 분자의 크기를 구할 수 있게 된다.

Autocorrelation

그렇다면, 산란광의 세기의 시간에 따른 변화를 어떻게 알 수 있을까? 여기서 autocorrelation을 사용한다. 이는 산란광의 빛의 세기가 시간에 의존적으로 변화한다는 것을 고속 광자 카운터로 측정하고, autocorrelation function으로 나타내어 보여준다. 우선 특정 시간 $t$에 대해 $\tau$만큼 경과시간이 흘렀다고 가정하자. 경과시간 이후의 광자의 세기가 시간 $t$에 측정한 광자의 세기와 얼마나 상관관계가 있는지를 나타내는 값을 다음과 같이 표현할 수 있다.

$\tau \rightarrow 0$이면, $\langle I_t^2\rangle$이 되고 이는 시간 $t$에 측정한 빛의 세기의 제곱이므로 최대값일 것이다. 만약 $\tau \rightarrow \infin$이면, $\langle I_t\rangle^2$으로 최소값이 된다. 지연 시간이 무한대에 가까워질수록 시간 $t$에 대한 상관관계가 사라진다고 볼 수 있기 때문에, 평균의 제곱이 된다. 실제로 분석기기에서는 컴퓨터에서 이 autocorrelation을 계산해주고 autocorrelation function을 이용하여 다음과 같이 나타낸다.

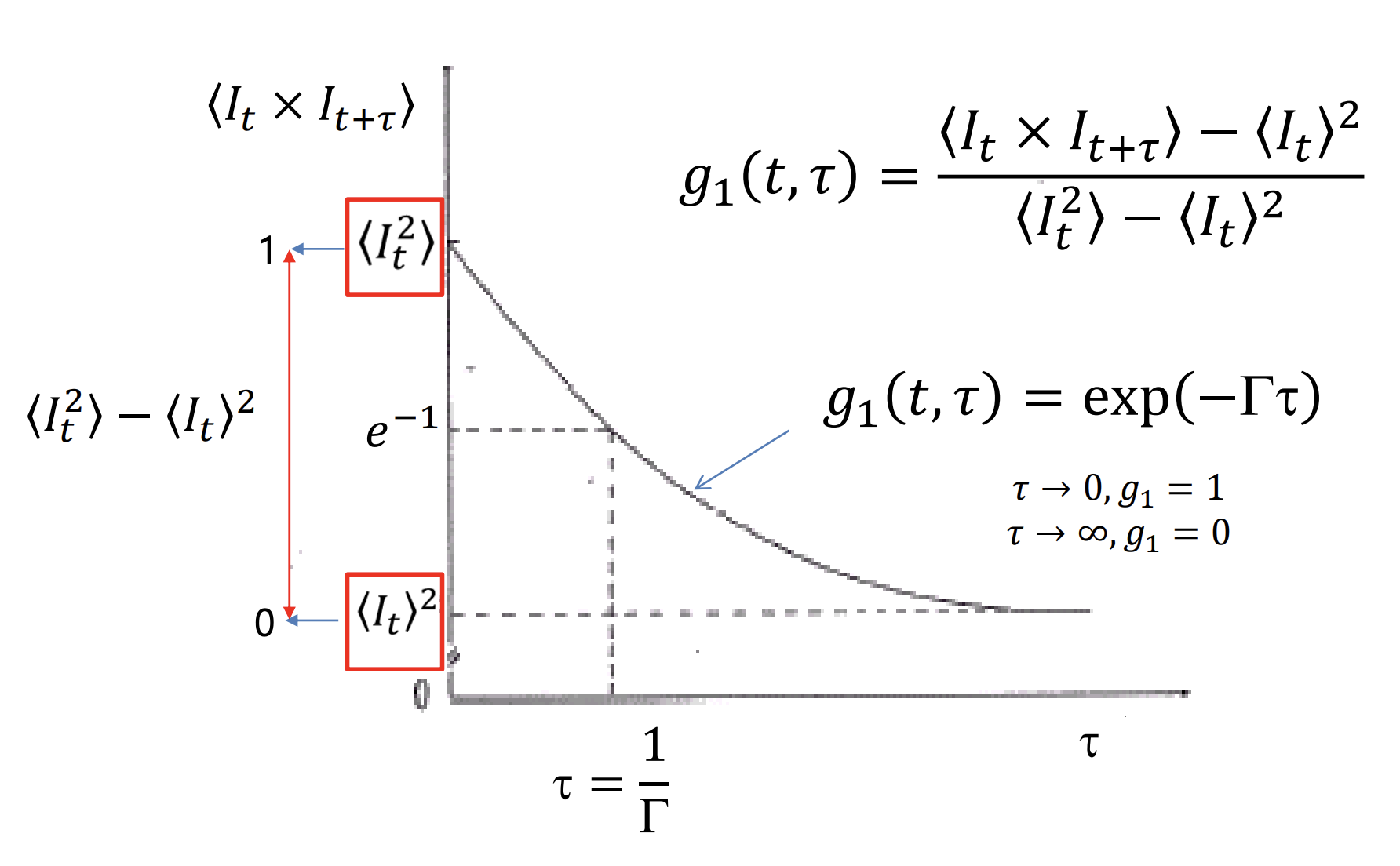
종속변수 $\tau$가 0일 때 최대이고, 무한대로 갈수록 exponentially decrease하기에, 산란광의 빛의 세기의 시간 의존적인 변화를 지수함수(exponential function)로 간단히 표현할 수 있다. 그 결과로 나온 지수함수를 autocorrelation function $g_1(t, \tau)$이라고 한다.

수식과 위의 그래프를 보면 알 수 있듯이, 최대값인 $\langle I_t^2\rangle$과 최소값(수렴값, base line)$\langle I_t\rangle^2$을 1과 0으로 두고 가장 간단한 지수함수로 나타낸 결과가 $g_1$이다. 이 때 $\Gamma$값에 따라 지수함수의 모양이 달라지게 된다.

$\Gamma$값이 크면 $\tau$가 증가함에 따라 $g_1$ 값이 더 빨리 감소한다. 이 말은 산란광의 세기의 시간적 의존도가 높다는 의미이다. 반대로 $\Gamma$값이 작으면 더 천천히 감소하고, 산란광의 세기의 시간적 의존도가 낮다는 의미이다. 즉, $\Gamma$는 산란광의 세기의 시간적 의존도를 의미하는 인자(parameter)라고 할 수 있다.

Siegert Relation

또 다른 autocorrelation function인 $g_2$를 sigert relation으로 정의할 수 있다. $g_1$과 $g_2$ 간의 관계를 siegert relation이라 하는데, $g_1$을 통해 $g_2$는 다음과 같이 정의된다.

$g_1$과 $g_2$ 모두 산란광의 세기의 시간적 의존도를 나타내는 함수이며, 두 함수의 관계성을 sigert relation이라 한다.

Diffusion coefficeint

어찌됐든 우리의 목표는 산란광의 세기의 의존도를 의미하는 $\Gamma$를 autocorrelation function을 통해 구할 수 있었고, 이를 통해 분자의 운동을 해석할 수 있다. 앞에서 $\Gamma$ 값이 클수록 의존도가 높게 나타난다고 하였다. 또한, autocorrelation function $g_1$에서 $\tau=\frac{1}{\Gamma}$이면 $e^{-1}$이므로, 시간과 $\Gamma$는 반비례 관계로 나타낼 수 있다. 그리고 픽의 확산 법칙(Fick's Law)에 의해 농도 계수(Diffusion coefficeint $D$)와 시간의 곱을 변화한 이동거리의 평균의 제곱으로 나타낼 수 있다.

The translational diffusion coefficient $D_t$ may be derived at a signle angle or at arangle of angles depending on the wave vector $q$.

$q$와 $\Delta x$의 관계는 우선 반비례 관계가 됨을 알아두도록 하자. 이에 대한 증명은 나중에 배우게 된다. 결론적으로, 우리는 $\Gamma$를 분자의 운동과 관련 있는 확산 계수로 나타낼 수 있게 되었다. 여러 detector의 angle에 따른 산란광의 세기를 DLS 방식으로 측정하여, autocorrelation function으로 $\Gamma$값을 측정할 수 있다. 이제 $q^2$을 종속 변수로 측정한 $\Gamma$를 외삽 혹은 선형회귀하면 기울기를 구할 수 있고, 이 값이 확산 계수 $D$이다. 이제 구한 확산 계수로 어떻게 분자량의 크기를 구할 수 있을까? 이는 Strokes-Einstein equation을 이용하여 구할 수 있다.

Strokes-Einstein equation

$D_t$ is often used to calculate the hydrodynamic radius of a sphere through the Strokes-Einstein equation.

위 식이 Strokes-Einstein equation이고, 우리가 구할 입자의 크기(분자량)은 $R$값이다. 이는 용액 상에서 고분자 입자가 용매와의 상호작용으로 인해 가지는 부피(shrink하거나 extended되어 가지는 부피)를 구라 가정하고, 그 반지름에 해당하는 유체역학적 부피(hydrodynamic radius)를 의미한다.

결국 우리는 DLS로 시간에 따라 의존적으로 변화하는 산란광의 세기를 측정할 수 있고, 이를 autocorrelation function을 이용해 $\Gamma$를 계산해 확산 계수 $D$를 구할 수 있었다. 그리고 최종적으로 particle의 크기에 해당하는 $R$값을 구할 수 있다.

Molecular weight from viscosity

점도계(viscometer)의 원리

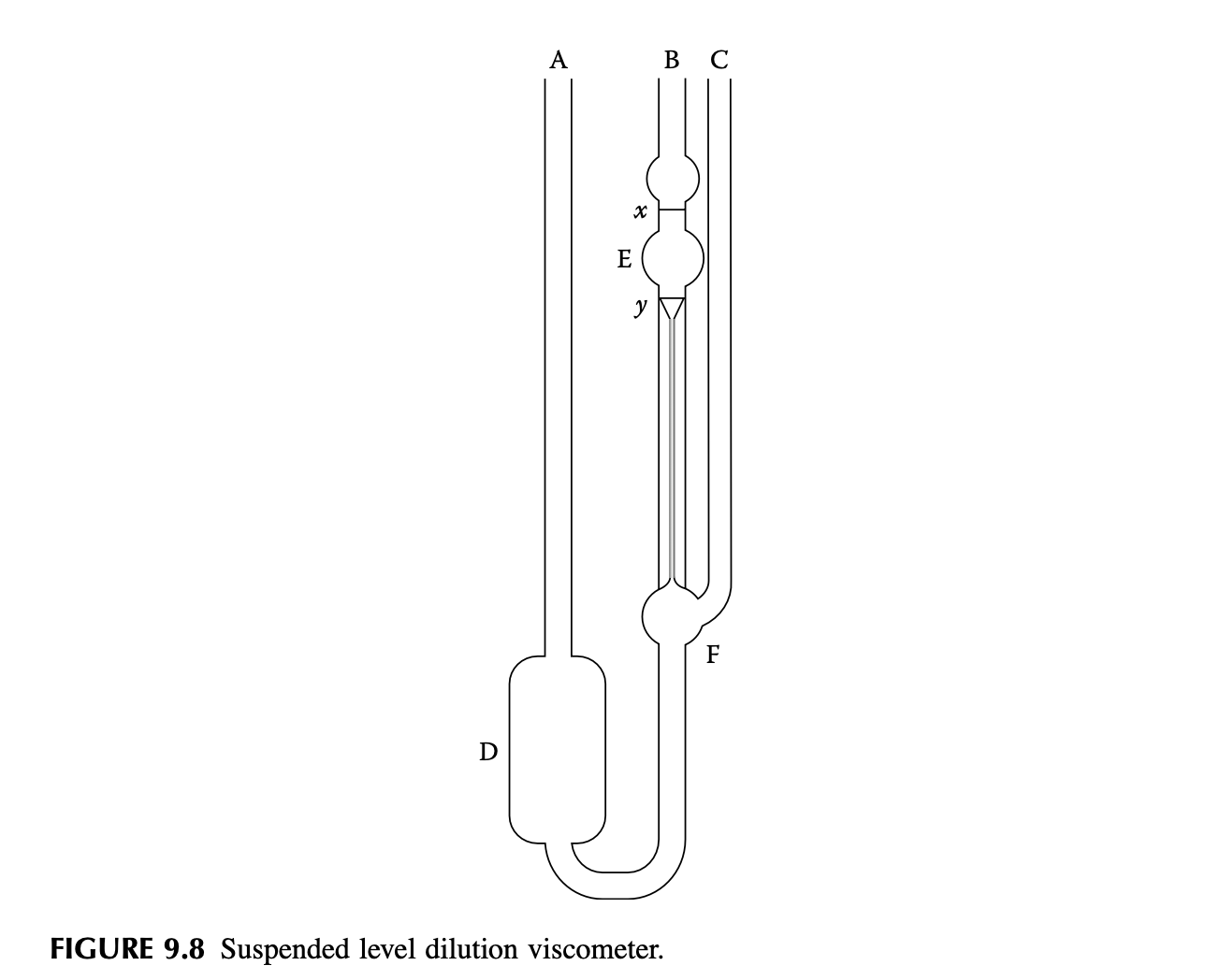
위 그림의 $x$에서 $y$로 유체가 흐르는 시간 $t$를 측정해 용액의 흐름 시간을 구할 수 있다. 이를 점도로 나타내는데, 직관적으로 점도가 높은 액체일수록 흐름에 저항하는 성질이 크기 때문에 흐름 시간이 크게 나타난다고 할 수 있을 것이다. 우선 용매(solvent)의 흐름 시간 $t_0$를 측정하고, 농도 $c$를 높여가며 용액(solution)의 흐름 시간 $t$를 측정하여 농도를 구할 수 있다.

Relative, Specific, Intrinsic Viscosity

이론적인 관점에서, 고분자의 농도 $c$가 0이면 용매의 점도 $\eta_s$와 용액의 점도인 $\eta$의 값이 같아야 하기 때문에, $c=0$이면, $\eta = \eta_s$이다. 또한 농도가 증가함에 따라 점도가 높아지는 것을 반영하기 위해 다음과 같은 다항식으로 점도를 나타낸다.

위 식에서 $[\eta]$는 절대 점도(Intrinsic Viscosity, 이하 IV)라 한다.

점도계로 측정한 점도는 얼마나 용액의 점도가 용매의 점도보다 높은지 상대적인 값을 알려주기에 상대 점도(relative viscosity)를 구할 수 있다. 이는 다음과 같은 식으로 나타낼 수 있다.

그리고 상대 점도의 최소값을 0으로 만들기 위해 $\eta_r$에서 1을 빼준 값인 비점도(specific viscosity, $\eta_{sp}$)를 다음과 같이 정의하자.

농도가 매우 낮은 묽은 용액(dilute solution)을 가정한다면, 비점도는 다음과 같이 나타낼 수 있다.

즉, 극한으로 표현하면,

이는 다음과 같이 비례 관계를 유도할 수 있다.

Mark Houwink eq

점도계로 측정한 $\eta_r$을 통해 $\eta_{sp}$를 구한 뒤, 외삽으로 IV, $[\eta]$를 통해 어떻게 분자량을 구할 수 있을까? 이는 Mark Houwink equation으로 구할 수 있다.

우선 위에서 $[\eta]M\sim V$하였다. $V$는 $R^3$에 비례하기 때문에, 최종적으로 분자량을 $R$의 제곱의 형태로 나타낼 수 있다.

Fractal Dimension

여기서 $D$는 프렉탈 차원(fractal dimension)값이다. 우리가 흔히 차원을 정의하는 1차원, 2차원, 3차원 등의 차원이 아닌 분수의 차원으로 나타낼 수 있을까? 하는 질문에서 프렉탈 차원이 시작되었다. 임의의 차원의 정의는 공간을 구성하는 독립 벡터인 기저(basis)의 개수로 구한다. 프렉탈 차원은 척도(scale)의 자기 유사성(self-similarity)를 통해 구한다. 이는 다음과 같다.

여기서 $\epsilon$은 자기 유사성을 가지는 척도를 의미하며, 이 값은 $1/2, 1/3, 1/4, \cdots$만 가능하다. 아래의 그림을 보면 이해가 될 것이다.

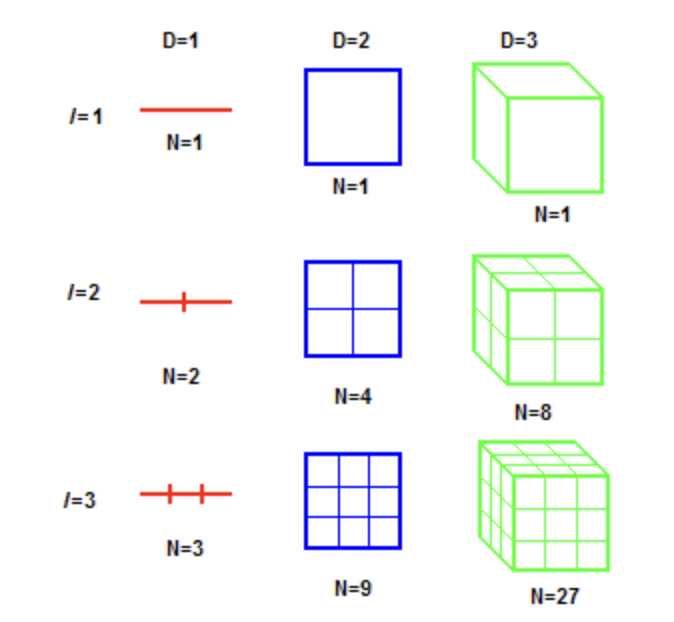
2차원 공간의 면적이 1인 정사각형을 척도를 줄여나가며, 자기 유사성이 있는 더 작은 사각형을 만든다. 이 때, $\epsilon=1/2$이면, $N=4$가 되기 때문에, $D = \log 4 / \log 2 = 2$로 2차원을 정의할 수 있다. 직선은 척도를 줄여나가도 D값이 1로 동일하기 때문에 1차원, 동일한 방법으로 정육면체는 3차원이 된다.

어찌됐든 분자량을 $R^D$로 나타낼 수 있기 때문에, $R$을 $M^{1/D}$라 볼 수 있다. 이를 이용해 다음과 같이 IV 값을 구할 수 있다.

Mark-Houwink equation은 다음과 같다.

여기서 $K$는 비례 상수가 되고, 이 식을 통해 우리는 절대 점도 IV값을 통해 분자량을 구할 수 있게 된다. 예를 들어 $\theta$-solvent의 경우에는 $D=2$로 정의되어 있기 때문에, $a = 3/2 - 1 = 0.5$의 값을 가진다. 그리고 good solvent의 경우에는 $D=5/3$이므로 $a$는 $0.8$정도의 값을 가진다.

유의할 점은 여기서 $M$은 vosicosity average molecular weight로 $M_v$로 나타낸다. 점도를 통해 고분자의 평균 분자량을 구한 방법이기 때문이다.

하지만, 우리는 절대 점도 IV값을 점도계로 측정한 $\eta_r$ 값의 외삽 혹은 선형 회귀로 구하게 된다. 그렇기에 실험 오차에 따른 정확도에 차이가 있을텐데 이를 확인하는 방법으로 Huggins and Krammer equation을 이용한다.

Huggins equation

Kramer equation

위의 Huggins equation은 위에서 정의한 상대 점도 $\eta_r$에서 1을 뺀 뒤 양변을 $c$로 나누어 구한 값이다. 상대 점도 $\eta_r$ 식의 양변에 $\ln$을 취하면,

우리는 $\log$의 Taylor series를 이용하면 위 식을 다음과 같이 나타낼 수 있다.

위 식에서 앞 두개의 항을 $c^2$으로 묶어주면,

Krammer equation은 다음과 같이 정의된다.

두 식을 통해 IV를 어떻게 결정할 수 있을까? 바로 외삽이다. 농도 $c$에 따른 Huggins equation을 이용한 값을 그린 그래프와 농도 $c$에 따른 Krammer equation을 이용한 값을 그린 그래프 2개를 외삽하면 두 그래프 모두 $y$절편 값이 $[\eta]$임을 알 수 있다. 아래와 같은 그래프를 보면 더 이해가 잘 될 것이다.

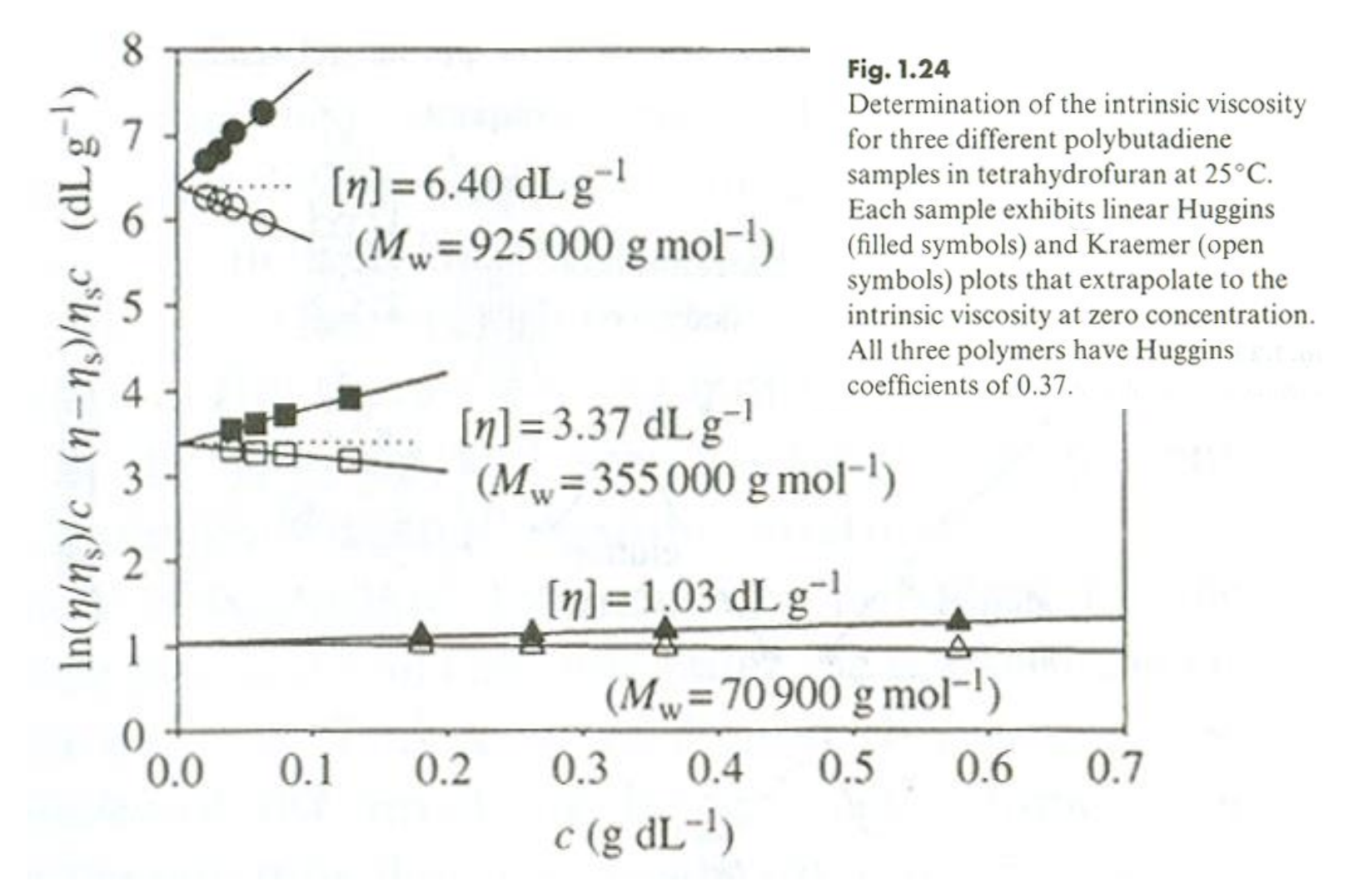
Viscosity-average molecular weight

이제 IV를 정확히 구하는 방법도 알았다. 그리고 IV는 Mark-Houwink equation을 이용해 분자량을 구할 수 있었는데, 이 분자량은 단분산(monodisperse)를 따르는 입자로 구성된 물질일 때 성립한다. 실제 고분자는 다분산(polydisperse)를 따르기 때문에, 다음과 같이 비점도를 정의할 수 있다.

여기서 $c_i$는 particle $i$의 농도를 의미하고, $c$는 전체 농도이다.

그럼 절대 점도, IV는 다음과 같다.

마지막 식에서 양변에 비례 상수 $K$를 나눠주면, 최종적으로 점도 평균 분자량(viscosity average molecular weight) $M_v$는 다음과 같이 정의할 수 있다.

우리는 고분자의 일반적인 분자량 분포 함수로 부터 $M_n < M_v < M_w$의 관계를 따른다고 배웠는데, 이 또한 위 식으로 유도가 가능하다. $a=1$이면, $M_v = M_w$와 같아지고, $a=-1$이면, $M_v = M_n$이므로, $0.5 < a < 0.8$ 사이에서 $M_n < M_v < M_w$가 성립한다.

정리

지금 우리는 고분자의 molar mass를 어떻게 구하느냐를 배우고 있다. 여기에 여러 방법들이 있고, $M_n$은 총괄성(colligative property)를 통해 구할 수 있었다. 여기서 concentration effect를 고려하여 비리얼 전개를 이용했었다. 또한 $M_w$는 빛 산란(light scattering)을 이용해 구할 수 있었는데, 이 때 static light scattering과 dynamic light scattering이 있고, 이번 시간에 배운 것은 DLS이다. 시간에 따라 의존적으로 변하는 산란광의 세기를 detector로 측정하여, 현탁액의 입자들은 브라운 운동(brownian motion)을 따르기에 확산 계수($D_t$)를 구할 수 있었다. Strokes-Einstein equation에 의해 입자의 크기에 따라 확산 계수가 결정되기 때문에 최종적으로 용액 상에 존재하는 입자의 크기, 유체역학적 반지름(hydrodynamic radius)를 구할 수 있었다.

또한 점도는 입자의 크기와 모양을 반영한다는 점을 이용하여, 절대 점도를 프렉탈 차원(fractal dimension)을 이용해 $R$의 제곱으로 구할 수 있었다. Mark-Houwink equation으로 절대 점도를 통해 최종적으로 분자량을 구하는 방법도 배웠다. 이 때, 점도계로 측정한 상대 점도로 비점도를 구하여 Huggins and Krammer equations로 어떻게 정확히 절대 점도를 구하는 방법도 배웠다.