고분자물리
1.[고분자 물리] Introduction to polymer science
고분자(polyemer)는 구성 반복 단위 중 하나 또는 몇 개를 추가해도 크게 달라지지 않는 일련의 특성을 제공하기에 충분한 양으로 서로 연결된 하나 이상의 원자 종 또는 원자 그룹이 여러 번 반복되는 것을 특징으로 하는 분자로 구성된 물질이다. 여기서 구조적으로 반
2.[고분자 물리] Chain Shape
고분자 사슬의 형태는 어떻게 결정될까? 아마 고분자 사슬이 어떤 구조를 가지느냐에 따라 달라지게 될 것이다. 고분자 사슬은 화학적 결합으로 구성되기에 화학적 결합에 의해 결정되는 분자 구조인, configuration과 고분자를 이루는 결합 각의 회전에 따른 형태 변화
3.[고분자 물리] Chain structure : chain model
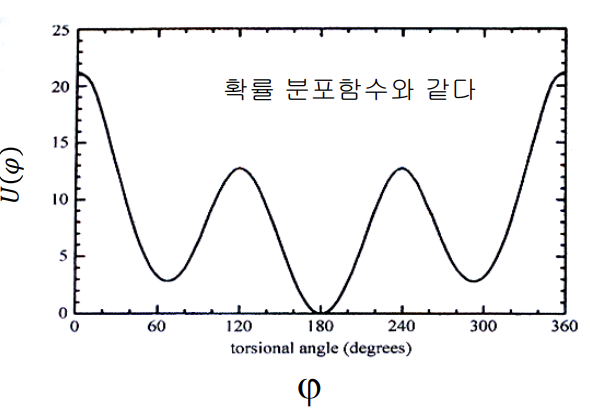
Introduction 고분자는 용융체(melt) 혹은 용액(solution)상태에서 $\sigma$ 결합의 rotation에 의해 random coil로 존재하며, 가장 안정적인 conformation을 유지하기 힘들다. 왜 그럴까? 가장 안정적인 conformat
4.[고분자 물리] Molar Mass
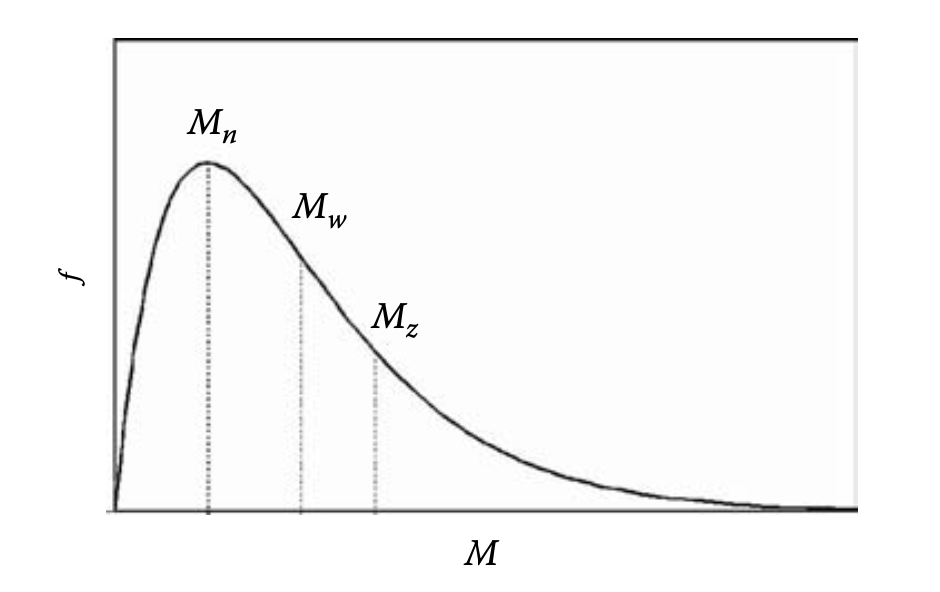
Introduction 고분자의 독특한 특성들은 사슬 구조로 긴 길이를 가지기 때문이다. 긴 길이를 가진다는 것은 즉, 큰 molar mass를 가진다는 의미이다. 하지만 고분자의 molar mass는 저분자 물질과 달리 하나의 값으로 고정되지 않고 분포를 이루기 때문
5.[고분자 물리] Chain Size - part 1
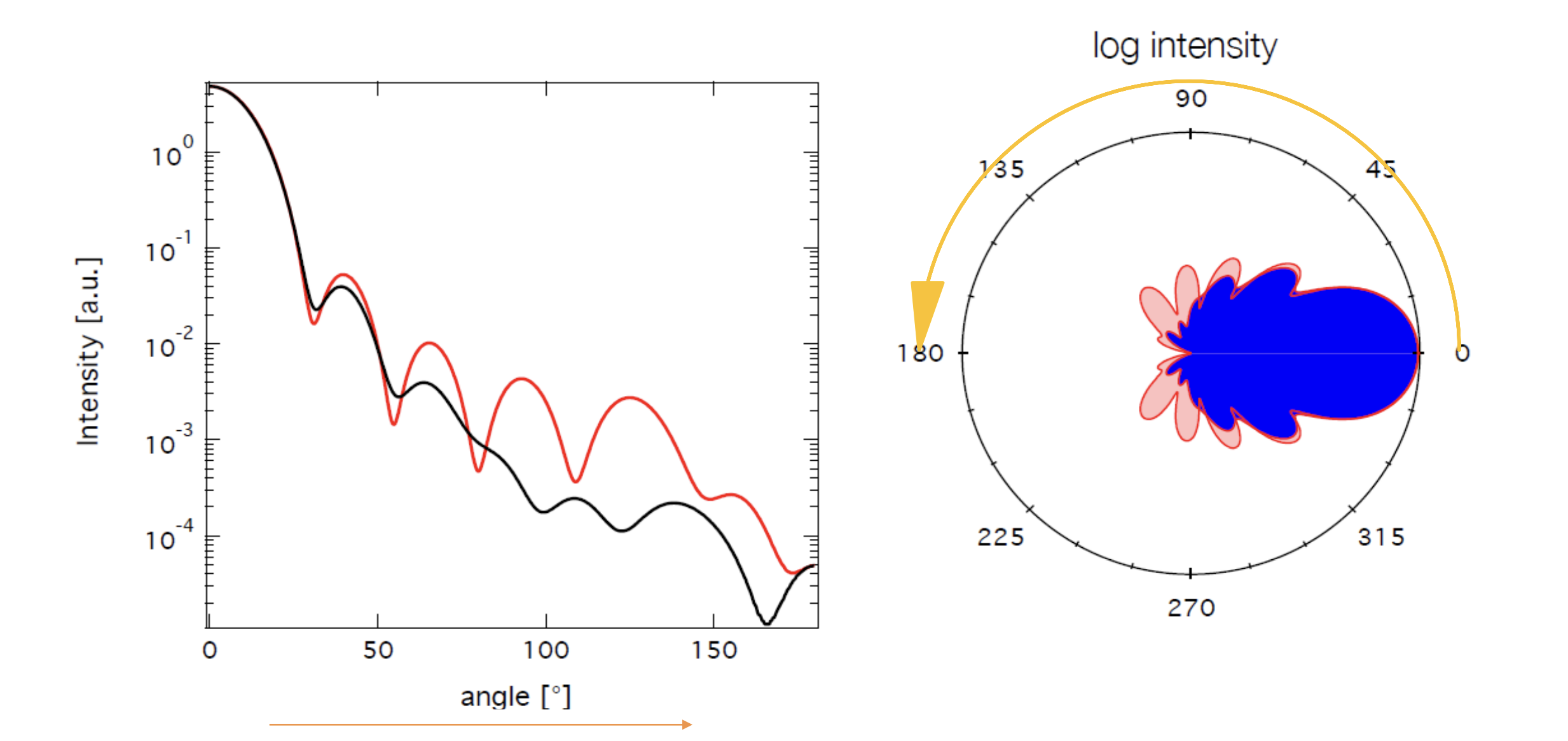
이전에 같은 고분자 물질이여도 용액 상에서 존재할 때, 용매의 solvent power에 따라 고분자의 크기, size가 달라진다고 하였다. 그 이유를 알아보자. 또한 size를 나타내는 parameter에는 1) End-to-end distance, $\\langle
6.[고분자 물리] Chain Size - part 2
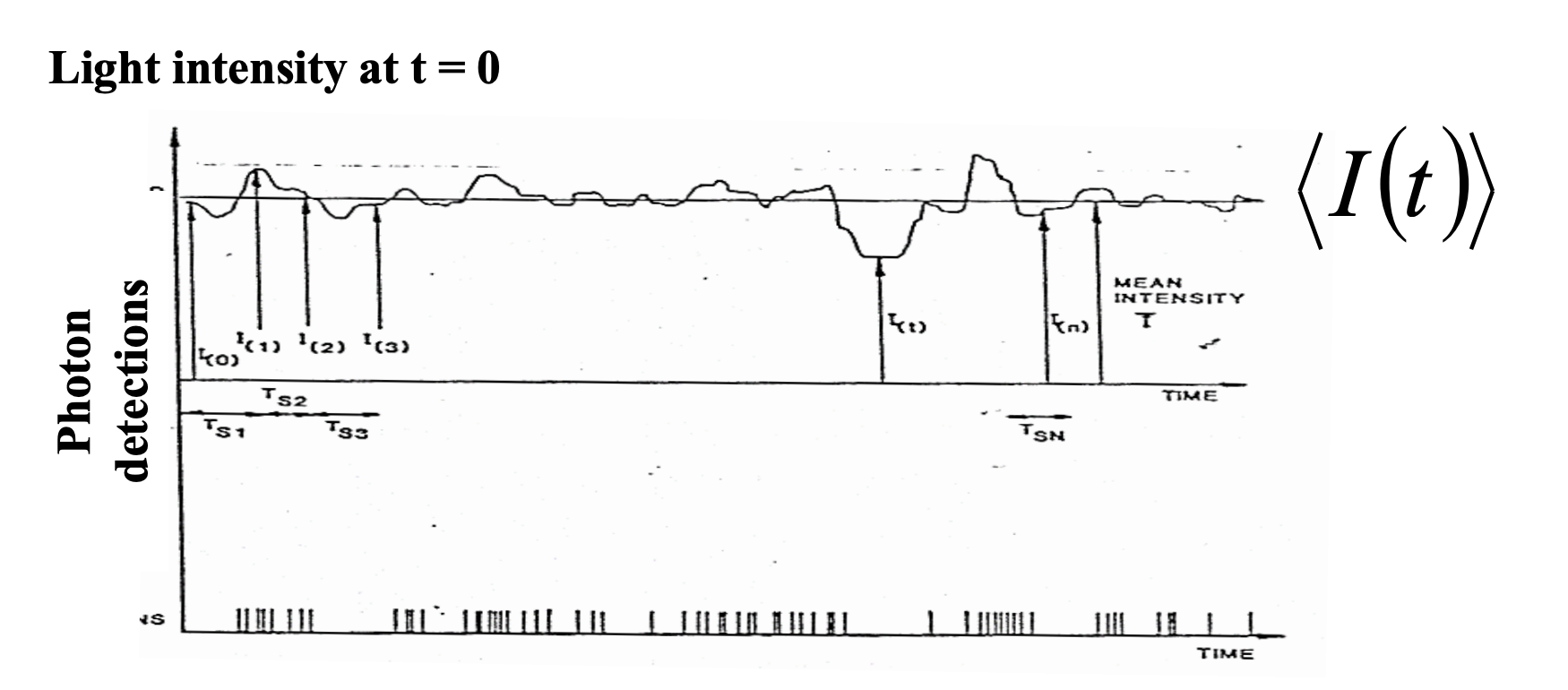
고분자의 molar mass를 구하기 위해 colligative properties를 이용해 수 평균 분자량 $M_n$을 구하였고, 입자의 크기 $d$가 파장의 크기 $\\lambda$보다 작은 경우, Reighleigh scattering인 경우에 어떻게 $M_w$를
7.[고분자 물리] GPC
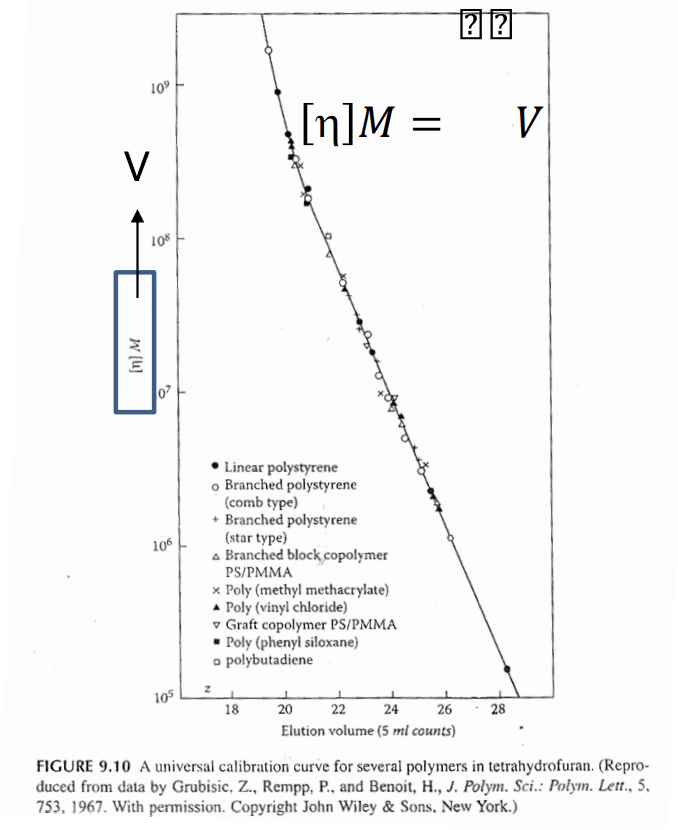
GPC(Gel Permeation Chromatography) Calibration Absolute Molecular weight를 구하는 방법 Universal Calibration Curve를 이용 Mark-Houwink Equation을 이용
8.[고분자 물리] Chain Conformation
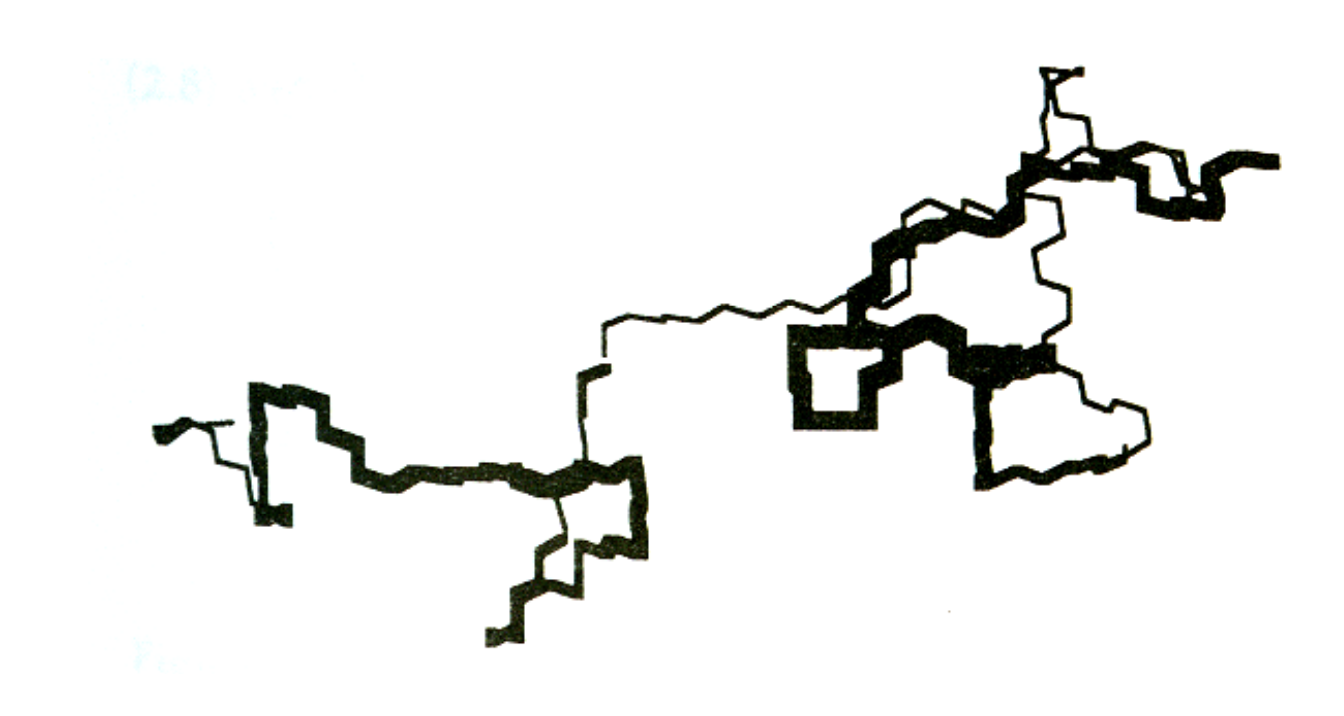
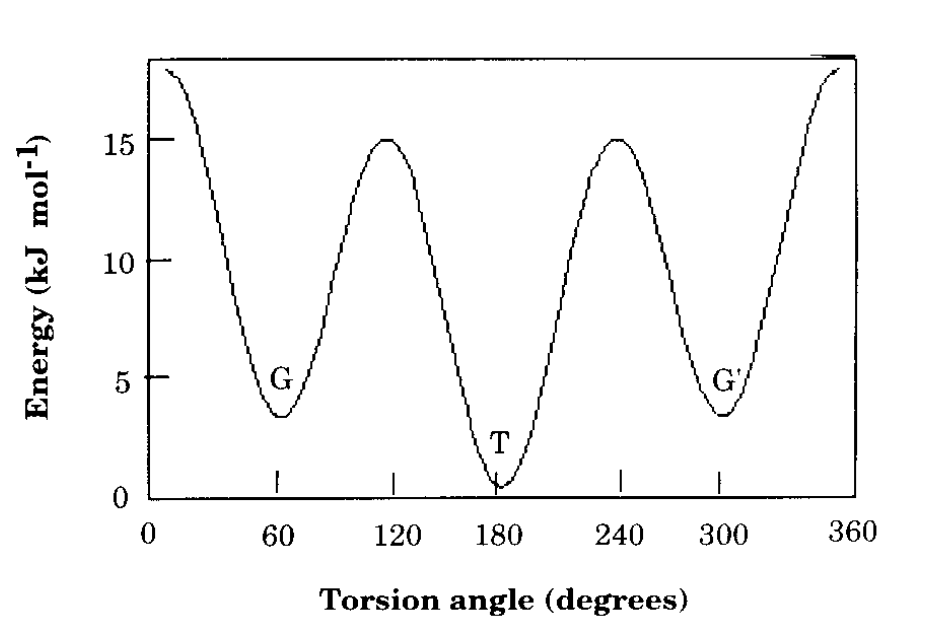
예전에 고분자 chain의 conformation에 대해 배웠다. conformation은 사슬의 축에 대한 rotation에 따라 달라지는 chain의 형태로, 열역학적 관점에서 안정적인 상태로 trans와 gauche 상태가 있다고 배웠고, all trans인 고분
9.[고분자 물리] Polymers in Solution - Flory Huggins Equation
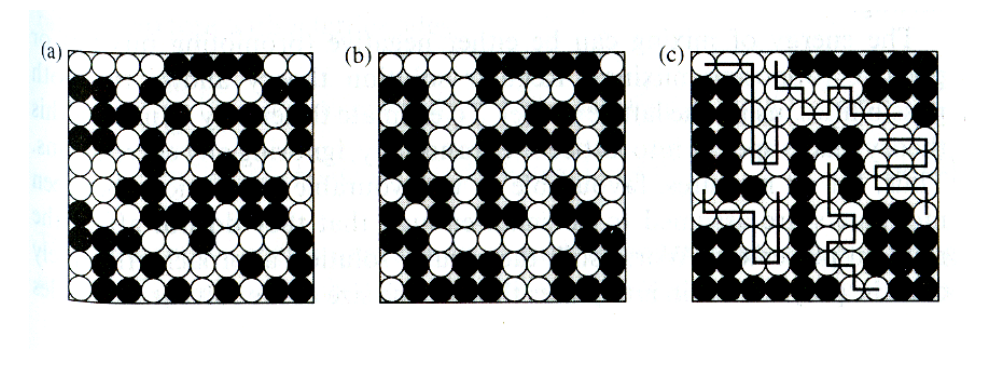
Thermodynamics 열역학에서 enthalpy와 entropy를 고려하여 Gibbs free energy, $G$는 다음과 같이 나타낸다. $$ G = H - TS $$ 그럼 2개 system을 섞는다고 가정하면, 섞은 후의 $G$와 섞기 전의 $G$의 차이인
10.[고분자 물리] Polymers in Solution - Phase Behavior
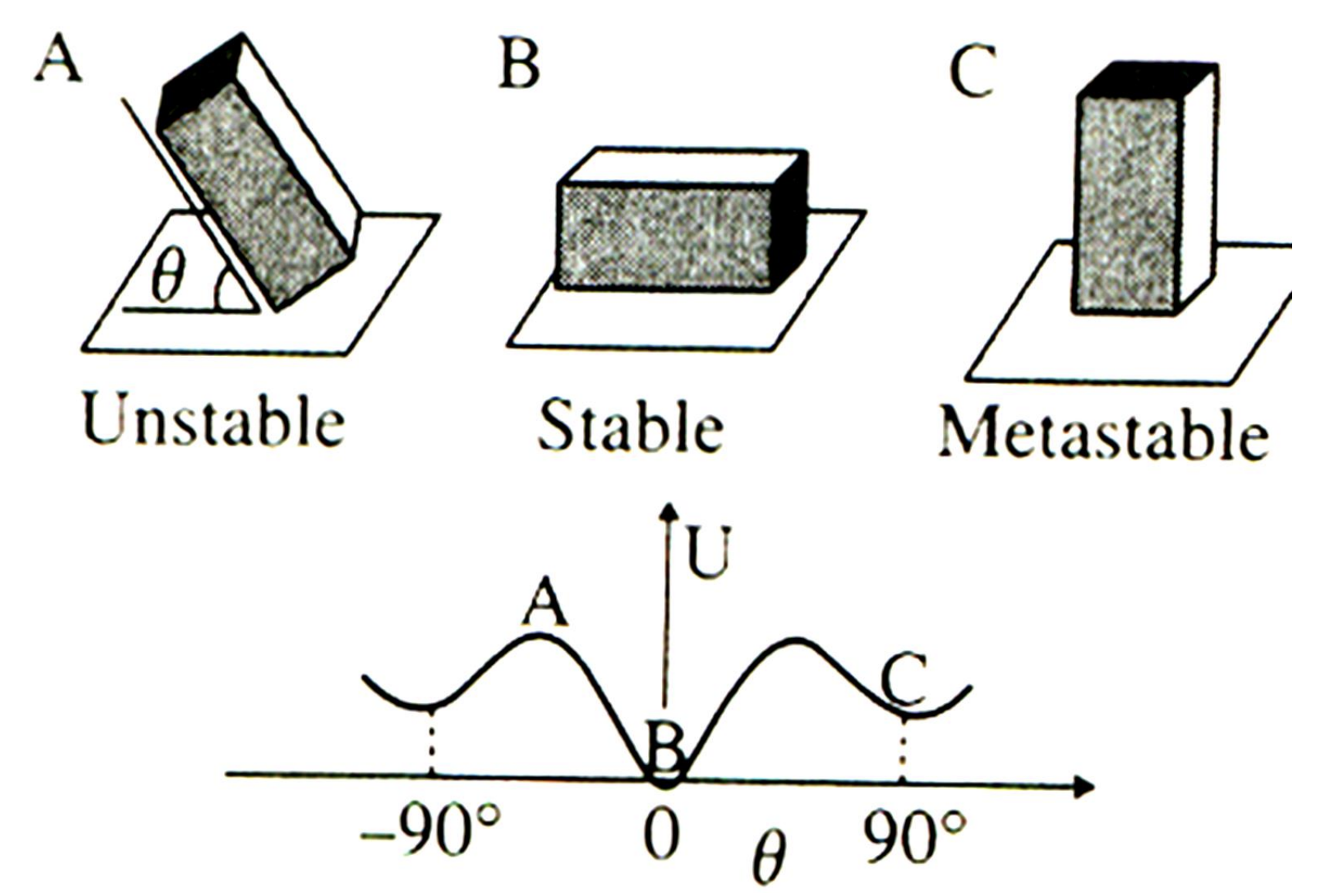
Flory-Huggins theory에서 Flory는 통계역학을 기반으로 lattice model을 사용하여, $\\Delta H, \\Delta S$를 구하여 polymer solution의 $\\Delta G^M$을 구하였다. 열역학적으로 자발적인 mixing은 $
11.[고분자 물리] Polymers in dilute solution

예전에 second virial coefficient로 $A_2$를 배웠었다. 이때 $A_2$가 증가하게 되면 good solvent를 의미하고 이는 solvent power를 증가시키기에 excluded volume도 마찬가지로 증가하게 된다. 그리고 Flory-Hu
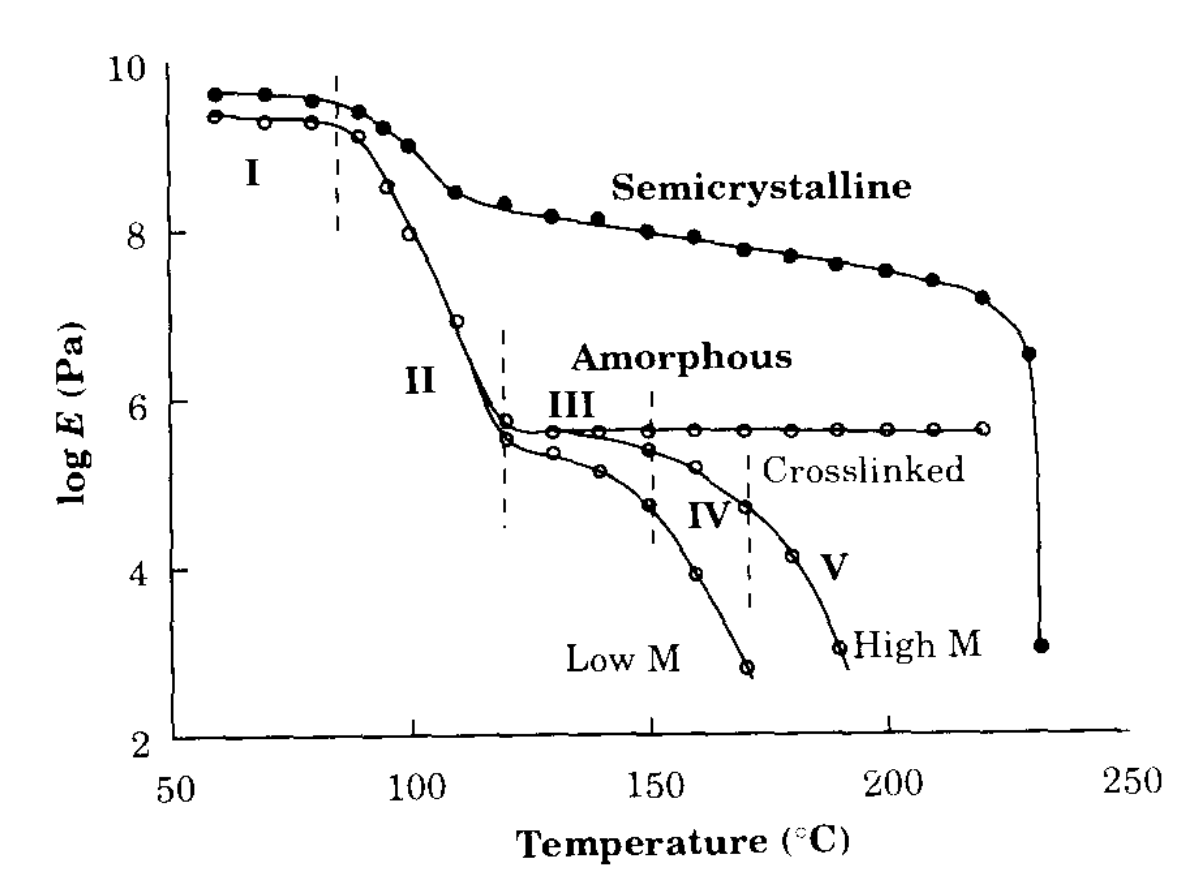
12.[고분자 물리] Viscoelastic Properties
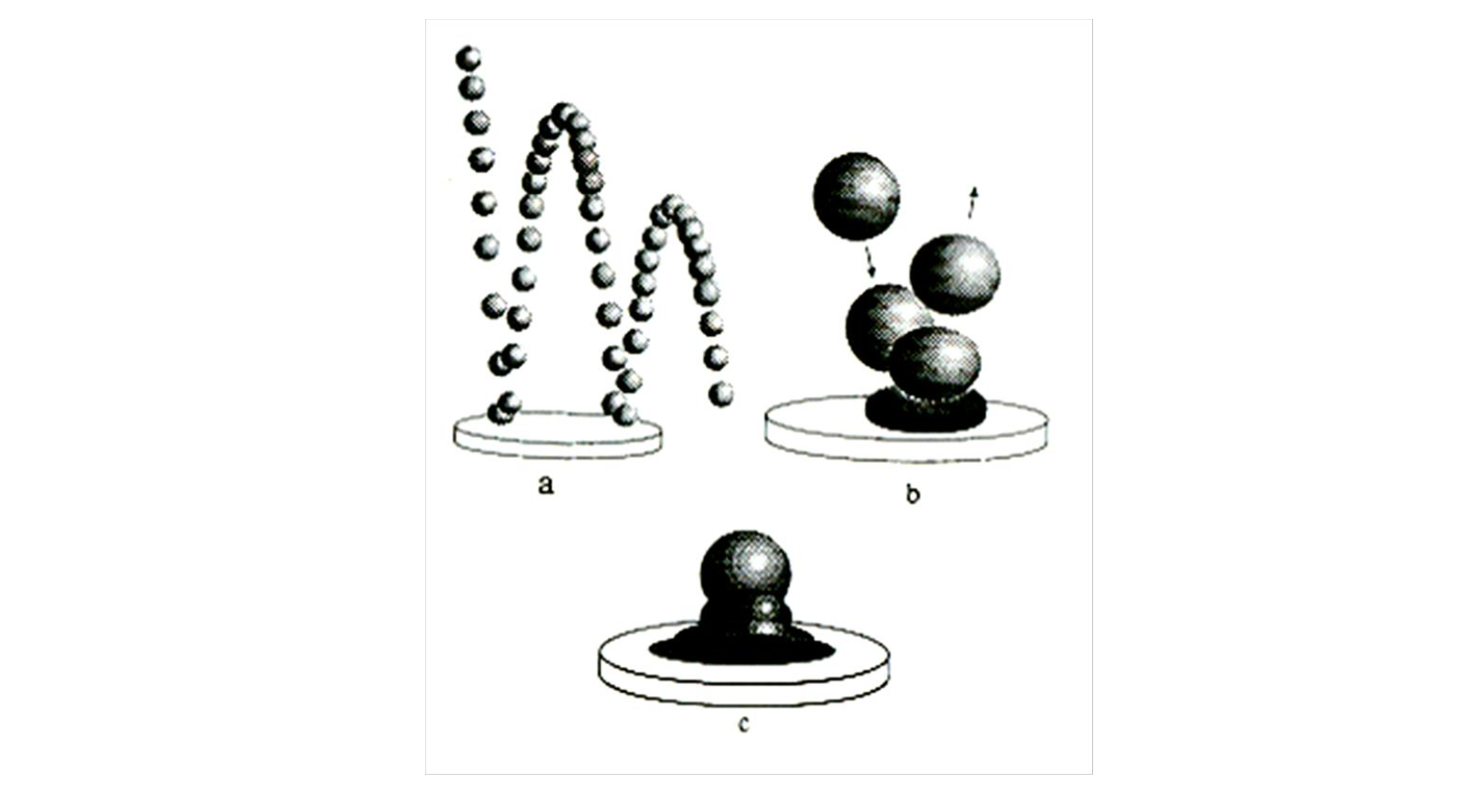
Introduction Rheology는 유변학으로 흐름과 변형을 연구하는 학문이다. 물체에 가해진 힘이 흐름과 변형으로 나타나는데, 이때 물체마다 나타나는 성질이 다르다. 흐를 수 있는 유체를 생각해보자. 유체에 어떠한 힘을 가하면 흐름이 발생할 것이고, 꿀처럼 점성
13.[고분자 물리] Maxwell Model
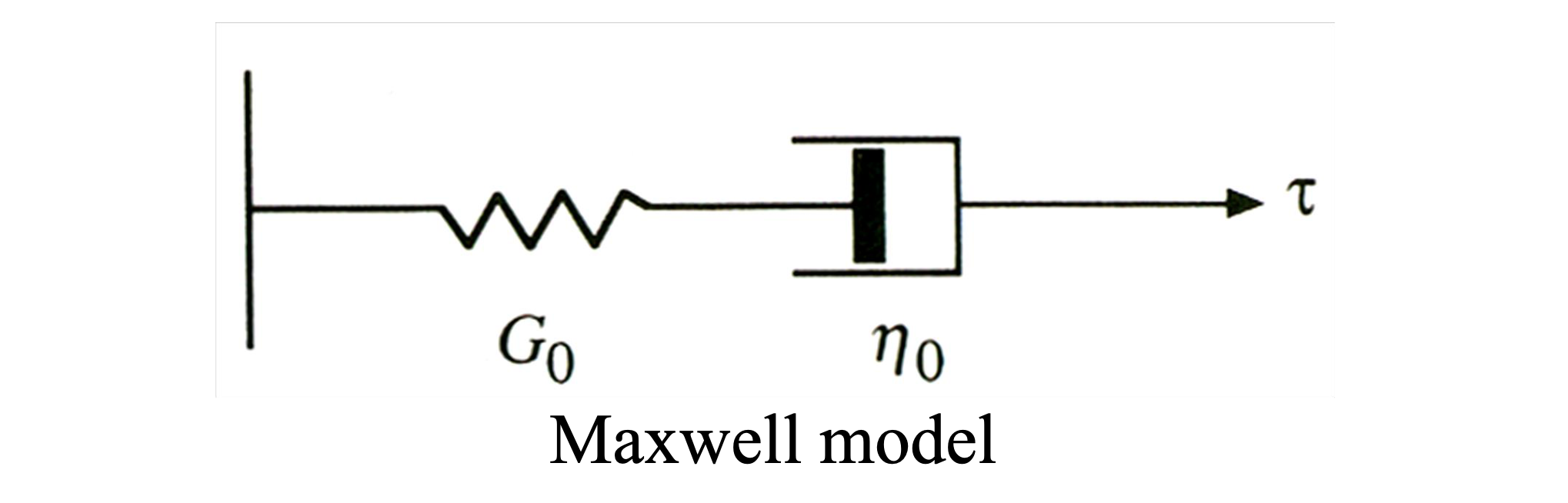
지난 시간에 점탄성의 띄는 물질은 어떤 거동을 보이고, 이는 time-dependent한 성질임을 확인하였다. 그리고 레오미터를 이용하여 여러 testing mode에 따라 strain과 stress를 측정할 수 있음도 배웠다. 마지막에 oscillation testi