GPC(Gel Permeation Chromatography)

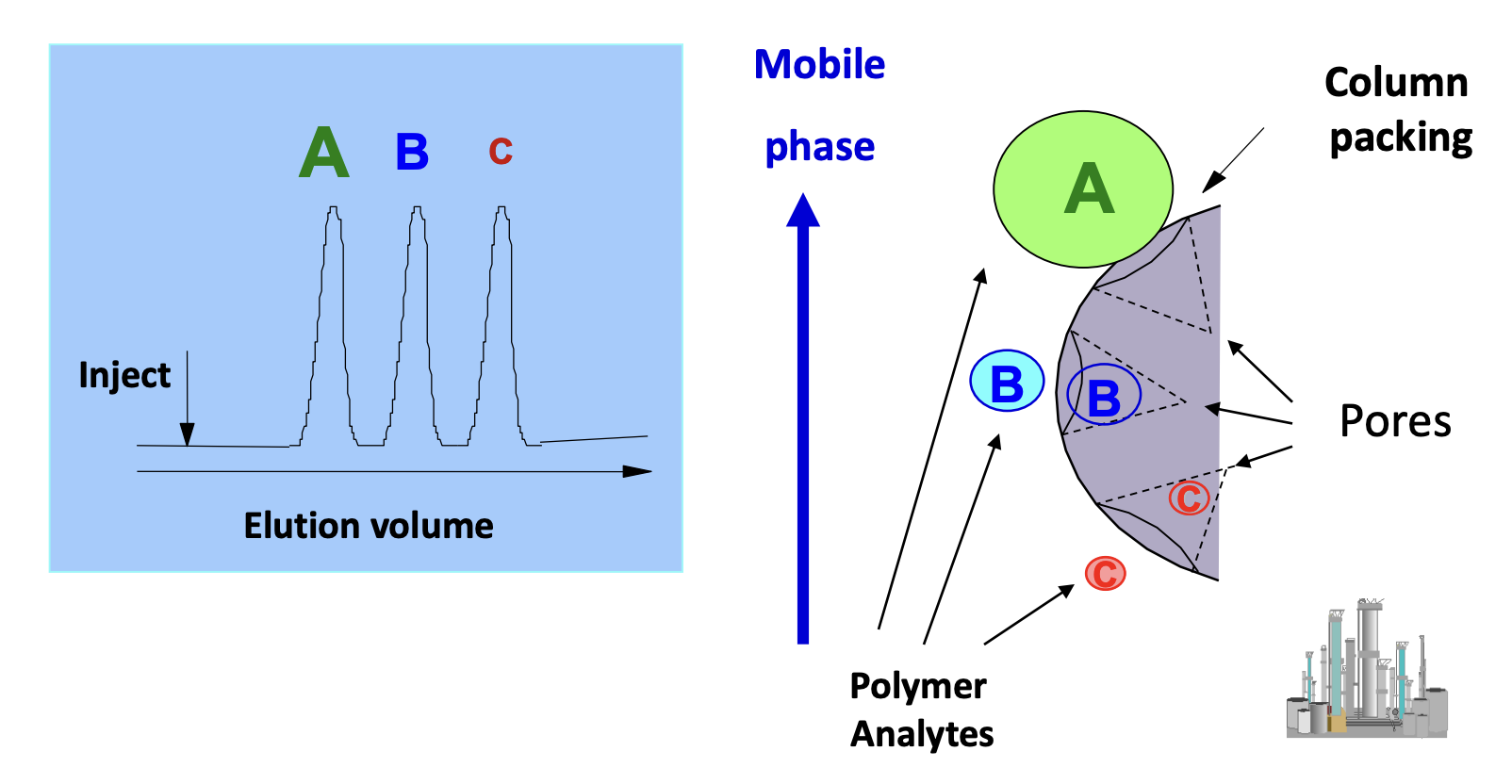
GPC는 고분자 물질의 절대적인 평균 분자량이 아닌 분포 함수를 구해주는 방법이라고 앞에서 배웠다. 그런데 GPC가 구한 분포함수도 절대적인 값이 아니라 상대적인 값이다. 이를 통해 어떻게 절대적인 $M_n, M_w, M_v$를 구할 수 있을지 알아보자.

우선 GPC의 구조는 위의 그림과 같고 좌측의 그래프가 GPC를 통해 얻을 수 있는 그래프이다. GPC는 column에 혼합물을 통과시키면서 크기에 해당하는 부피에 의해 분리시켜주는 방법이다. column 내에는 다공성 pores가 존재한다. 고분자 물질의 크기는 용매와의 상호작용으로 인해 차지하는 부피가 다르기에, 다양한 분자량을 가지는 고분자 물질이 용질로 녹아 있는 혼합물을 column에 통과시키면, 부피가 큰(=분자량이 큰) 고분자 물질은 다공성 pores를 통과하지 못하고 빠르게 이동상의 흐름을 따라 column의 밑에 빠르게 도착하게 될 것이다. 반대로 부피가 작은 고분자 물질은 다공성 pores를 이리저리 통과하며 column의 밑에 늦게 도착하게 될 것이다. 즉, 고분자 물질의 크기(부피)에 따라 column을 통과하는 시간이 달라지기에 size exclusion chromatography라고도 부르는 것고, 이 시간을 측정하여 서로 다른 분자량을 가지는 고분자 물질의 분포함수를 구할 수 있게 되는 것이다.

좌측의 그래프를 보면 Elution volume이라고 되어 있는데, 이는 GPC에서 이동상을 따라 column 밖으로 나온 혼합물의 부피로, 시간에 따라 이동상이 흐르면서 일정한 속도로 column의 밑으로 넣어준 혼합물이 빠져나올 것이기 때문에, 이를 시간과 같은 개념으로 봐도 무방한 것이다. 이렇게 분포 함수를 구할 수 있다는 것은 좋은 점이지만, 큰 단점은 바로 절대적인 값이 아닌 상대적인 값이라는 것이다. 그 이유는 GPC를 통해 얻은 데이터는 무게에 기반한 측정결과로 얻은 값이 아니라 부피에 기반한 값으로 얻은 데이터이기 때문이다. 이를 어떻게 해결할까?

Universal Calibration Curve

여기서 우리는 universal calibration curve를 이용한다. 앞에서 우리는 IV값과 분자량에 대해 다음과 같은 비례 관계를 정의했었다.

이를 어떠한 비례상수로 새로운 식을 새우면,

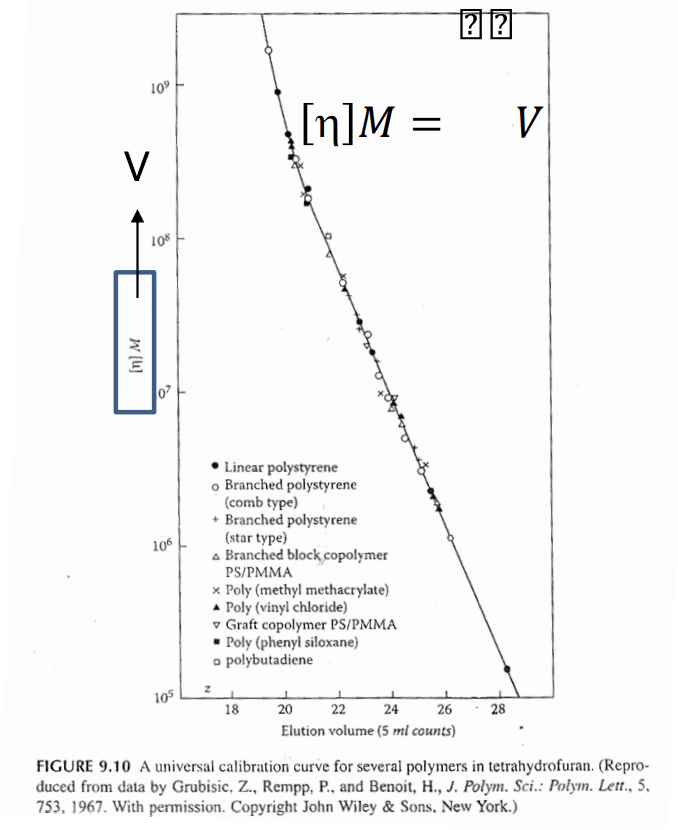
그리고 위에서 얻은 식을 따라 elution volume($V_e$)에 따른 측정한 IV 값과 분자량을 곱한 V로 plot한 결과, 고분자의 종류에 관계 없이 하나의 master curve가 얻어진다. 즉, 임의의 시료에 대해 $[\eta]M$의 값이 같으면 수력학적 부피 $V$의 값도 같아지게 되고 이는 GPC로 측정할 경우, 같은 $V_e$에서 column을 빠져나온다는 의미이다.

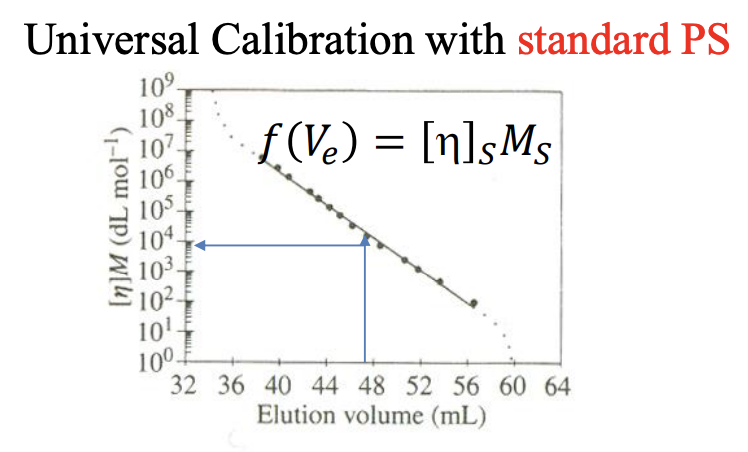
Universal Calibration은 PS처럼 분자량의 분포가 좁아 비교적 정확한 평균 분자량을 구할 수 있는 물질을 표준(standartd)로, GPC를 통해 얻은 standard PS가 $V_e$에 따른 $[\eta_S]M_s$를 $V_e$에 대한 어떤 곡선(함수), $f(V_e)$를 그려놓는다. 앞에서 설명했듯이 측정하고자 하는 물질의 $V_e$에 따른 $[\eta]_AM_A$값이 $f(V_e)$값과 같기 때문에 다음과 같은 식을 세울 수 있고,

최종적으로 어떤 임의의 물질 $A$의 분자량, $M_A$는 다음과 같다.

Mark-Houwink Equation을 이용하는 방법

universal calibration curve를 이용하여

로 $A$의 절대적 평균 분자량을 구할 수 있다 하였다. 그런데 만약 universal calibration curve를 얻지 못하는 경우에는 위 식에서 어떻게 절대적인 평균 분자량을 구할까? 우선 우리는 Mark-Houwink Equation이 다음과 같다 배웠다.

위 식을 통해,

를 다음과 같이 바꿔줄 수 있다.

다만, 위 방법은 표준 물질과 측정하고자 하는 물질의 Mark-Houwink 비례 상수인 $K$값과 fractal dimension을 이용해 구했던 $a$값을 모두 알고 있어야 한다는 전제 조건이 따른다.