[고분자화학] 2-2 Kinetics of Step Polymerization

jmt·2024년 4월 14일

고분자화학

목록 보기

4/27

Carother Equation

지난 시간에는 step polymerization의 mechainsm이 stepwise하게 서로 다른 크기의 종(species; monomer, dimer, trimer, ...)의 반응으로 고분자가 형성된다는 것을 배웠다. 그리고 step polymerization의 kinetics를 고려할 때, 서로 다른 크기이면 같은 반응기의 반응성이 달라지지 않을까? 하였지만 experimental evidence로 분자의 크기와 functional group의 반응성은 독립적임을 배웠다. 그렇다면, 시간에 따라 중합이 일어나는 step polymerization의 속도를 식으로 정의해보자.

Extent of Reaction

extent of reaction을 $p$ 로 표기하며, 이는 시간 $t$ 에 대해 functional group(반응기)들이 얼마나 반응했는가를 나타낸다. 그래서 전환률 혹은 반응 진척도라 부르고, 전환률은 반응기가 초기 농도에 비해 반응하지 않은 양을 나타낼 수 있다. 예를 들어 시간 $t$ 에서 어떤 반응기의 농도를 $[M]$ 이라 표현하면,

[M] = [M]_0 - [M]_0 p = [M]_0 (1-p)

로 나타낼 수 있을 것이다. 즉 전환률 $p$ 는 정의에 따라

p = \frac{[M]_0-[M]}{[M]_0}

가 되는 것이다.

Number-Average Degree of Polymerization

또한 위에서 정의한 전환률을 이용하여, 시간 $t$ 에 따른 중합 정도를 식으로 나타낼 수도 있을 것이다. 이런 수평균 중합도를 $\bar{X}_n$ 으로 표기하며, 시간 $t$ 에 따른 중합 정도는 초기의 monomer 갯수가 시간 $t$ 가 지나서 반응하지 않은 monomer에 비해 어느정도 였는 지를 나타내면 알 수 있을 것이다. 이런 정의에 따라

\bar{X}_n = \frac{N_0}{N} = \frac{[M]_0}{[M]}

그런데 위에서 정의한 전환률 $p$ 를 이용하여 시간 $t$ 의 반응기의 농도 $[M]$ 은 $[M]_0 (1-p)$ 로 나타낼 수 있다고 배웠으므로,

\bar{X}_n = \frac{1}{(1-p)}

로 나타낼 수 있다. 전환률과 수평균 중합도를 나타낸 이 식이 바로 Carother Equation이다. 식을 보면 알 수 있지만, 대략 $p > 0.99$ 정도 되어야 $\bar{X}_n$ 이 100 정도 되는 것을 확인할 수 있다.

Polyesterification

이제 step polymerization의 kinetics를 알아보기 위해, polyersterification을 예시로 알아보자. polyersterification은 대부분의 step polymerization처럼 평형 반응이다. 반응속도를 높이기 위해 산 촉매를 사용한다.

1. Protonation of carboxylic acid

dialcohol과 diacid, 두 monomer를 사용해 중합하는데, 여기에 산 촉매를 사용하는 경우, 가장 먼저 diacid의 caboxylic acid가 산 촉매에 의해 protonation이 된다.

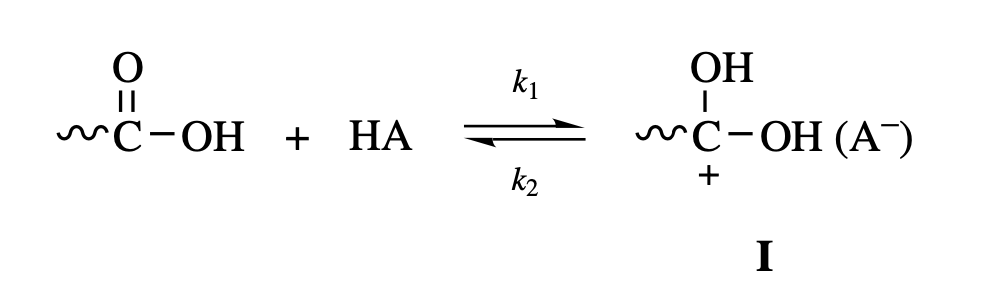
위 반응에서 $k_1$ 이 정반응, $k_2$ 가 역반응 반응 속도 상수가 된다. step polymerization의 대부분 반응들은 평형 반응이기 때문에, 정반응 속도와 역반응 속도가 같다. 즉, 다음과 같이 쓸 수 있다.**

\begin{aligned} v(\text{rate of forward reaction}) &= k_1[COOH][HA]\\ &= k_2[C^+(OH)_2] \end{aligned}

평형상수( $K$ )의 정의에 따라

K = \frac{[C^+(OH)_2]}{[COOH][HA]}= \frac{k_1}{k_2}

가 됨을 확인할 수 있다.

2. Reaction of Protonated Species with Alcohol

Protonated Species( $\text{I}$ )와 알코올이 반응하여 ester를 만드는 것이 그 다음 반응이다.

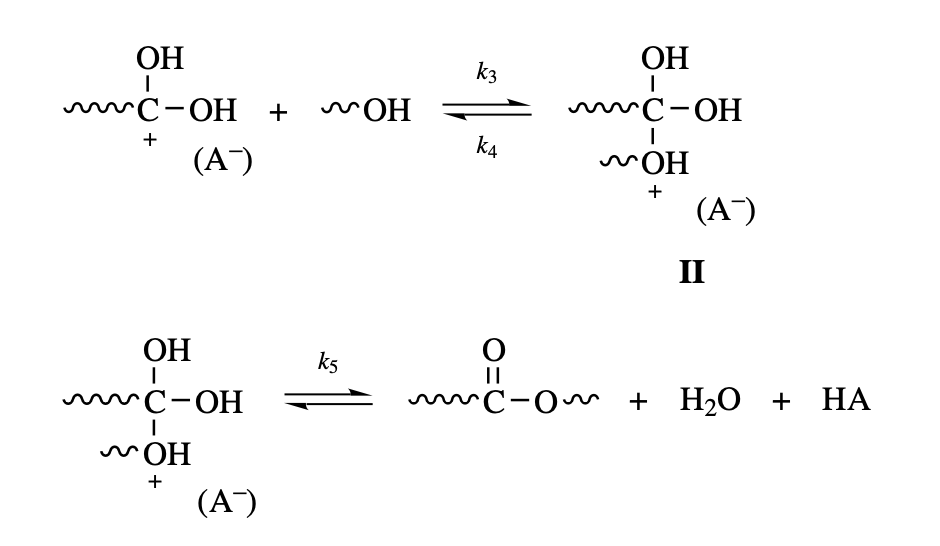
이 때, $\text{I}$ 과 알코올이 반응하는 정방향 $k_3$ 와 역방향 $k_4$ 가 존재하고, 생성된 ester가 counter ion( $A^-$ )로 인해 ester linkage를 가진 polymer와 small molecule $H_2O$ 와 산촉매 $\text{HA}$ 를 다시 내놓는 정방향 $k_5$ 가 존재한다. 여기서 $\text{I}$ 과 알코올이 반응하는 정방향 반응은 상당히 느리게 일어나는 반응으로 $k_3$ 가 상당히 작은 값이 된다.

Rate-Determining Step

그렇다면, 위 반응에서 $k_4, k_5$ 는 어떻게 될까? 그리고 왜 $k_5$ 의 역반응 속도 상수인 $k_6$ 는 없을까? 그 이유는 높은 분자량의 polymer를 얻기 위해 위 반응에서 small molecule인 $H_2O$ 를 제거해주기 때문이다. 반응물을 지속적으로 제거해주기 때문에 위 반응은 르샤틀리에 원리에 의해 평형 반응은 지속적으로 정방향 반응만 일어나게 된다. 즉, 역반응인 해중합(depolymerization)은 일어나지 않게되고, 이에 따라 $k_4$ 도 존재하지 않게 된다. 결론적으로 $H_2O$ 의 제거로 정방향 반응만이 지속되어 중간체 $\text{II}$ 이 계속 중합되기 때문에, $k_4$ 는 무시할 수 있다.

polyesterification은 $k_1, k_2$ 반응은 상당히 빠른 속도로 일어나기 때문에 상당히 큰 값을 갖게 되고, $k_5$ 도 물을 제거해줘서 큰 값을 갖게 된다. 그럼 $k_1, k_2, k_5$ 에 비해 $k_3$ 값은 작은 값으로 전체 polyersterification에서 속도를 결정하는 단계는 $k_3$ 가 된다.

Rate of Step Polymerization

그럼 step polymerization(polyesterification)의 반응 속도를 어떻게 나타낼 수 있을까? 반응하는 functional group의 농도로 표현할 수 있게 된다. 즉, polyesterification은 시간 $t$ 에서 반응하지 않은 caboxyl group을 염기로 적정하여 그 농도를 알 수 있다면, 중합 반응의 속도를 알 수 있게 된다.

R_p = -\frac{d[\text{COOH}]}{dt}

앞에서 속도 결정 단계(RDS)는 $k_3$ 에 대한 반응이므로, 반응 전체의 속도는 $k_3$ 반응에 의해 결정된다.

-\frac{d[ \text{COOH}]}{dt} = k_3 [\text{C}^+(\text{OH})_2][\text{OH}]

하지만, $[\text{C}^+(\text{OH})_2]$ 는 반응 중간에 생성되는 중간체로 측정하기 어려울 것이다. 애초에 우리의 목표는 반응하지 않은 카복실기 group의 농도를 염기로 측정하여 $R_p$ 를 나타내고자 하였다. 그러므로, 위에서 정의한 평형상수 $K$ 를 위 식에 대입하면, polyesterification의 반응 속도 $R_p$ 는 다음과 같다.

R_p = -\frac{d[\text{COOH}]}{dt} = k_3K[\text{COOH}][\text{OH}][\text{HA}]

Self-Catalyzed Polymerization

polyesterification에서 외부 산 촉매(external catalysis)가 없다면, diacid의 monomer가 esterfication 반응에서 산 촉매로 작용하게 된다. 이를 자가 촉매 중합 반응이라 하고, 이 경우에는 $R_p$ 에서 $[\text{HA}]$ 가 $[\text{COOH}]$ 로 바뀌게 될 것이다. 그럼,

-\frac{d[\text{COOH}]}{dt} = k[\text{COOH}]^2[\text{OH}]

위 식에서 $k_3$ 와 $K$ 의 곱을 $k$ 로 간단히 나타내었다. 대부분의 중합 반응에서 두 개의 반응기 농도는 동몰에 가깝다고 가정하기 때문에,

[\text{COOH}] = [\text{OH}] = [\text{M}]

라 표현하자. 그럼 위 식은 아래와 같이 간단히 나타낼 수 있고,

-\frac{d[\text{M}]}{dt}=k[\text{M}]^3

적분한 결과는

2kt = \frac{1}{[\text{M}]^2} - \frac{1}{[\text{M}]_0^2}

이다. 여기서 Carother equation을 사용하여 전환률 혹은 수평균 중합도로 나타내면 다음과 같은 최종식을 얻을 수 있다.

\bar{X}_n^2 = \frac{1}{(1-p)^2} = 2[\text{M}]_0^2kt + 1

External Catalysis of Polymerization

그렇다면 외부 촉매가 존재한다면 어떻게 달라질까? 사실 $[\text{HA}]$ 를 $[\text{COOH}]$ 로 바꾸지 않고, 식을 유도하면 된다. 나머지 과정은 동일하다. $[\text{HA}]$ 가 외부 촉매이기 때문이다. 다만, 촉매의 농도는 중합 반응이 진행되면서 유지된다. 그 이유는 마지막 $k_5$ 반응에서 ester와 counter ion으로 $\text{HA}$ 이 다시 생성되기 때문이다. 즉, $k \times [\text{HA}]$ 를 또 다른 상수 $k^{\prime}$ 으로 나타낼 수 있다.

-\frac{d[\text{M}]}{dt}=k^{\prime}[\text{M}]^2

적분한 결과는

k^{\prime}t = \frac{1}{[\text{M}]^2} - \frac{1}{[\text{M}]_0^2}

이고, Carother equation을 사용하여

\bar{X}_n = \frac{1}{(1-p)} = [\text{M}]_0k^{\prime}t + 1

로 나타낼 수 있다.

Self vs Externally-Catalyzed

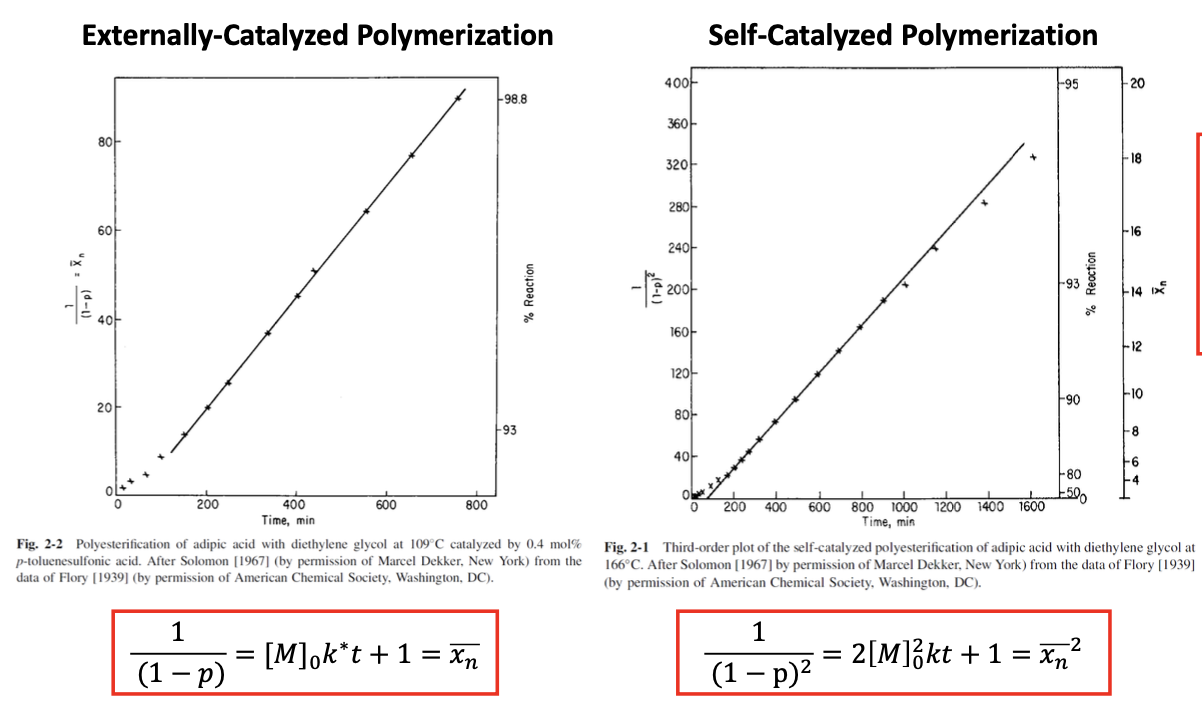
외부 촉매 사용 시 시간에 따른 중합도가 선형 관계가 됨을 알 수 있다. 하지만 자가 촉매 polymerization의 경우에는 $\frac{1}{2}$ 에 비례한다. 즉 선형관계가 아니게 된다. 이것의 의미는 위 그래프를 참고하여, 두 반응 모두 동일한 시간 800분이 지났다고 가정했을 떄, 외부 촉매를 사용한 경우에는 전환률이 약 99%에 가깝다. 그러므로, $\bar{X}_n = 1/(1-0.99) = 100$ 정도가 된다. 그에 반면, 자가 촉매를 사용한 경우에는 800분이 지난 시점에 전환률이 약 92%정도 밖에 되지 않는다. 그럼 수평균 중합도 $\bar{X}_n = 1/(1-0.92) = 1/0.08 = 12$ 이다. 높은 분자량을 같는 고분자가 되기 위해서는 수평균 중합도가 거의 100은 되어야 하는데 자가 촉매 중합 반응을 하게 되는 경우 상당히 많은 시간이 필요함을 알 수 있다.