[고분자화학] 2-4 Equilibrium Considerations

jmt·2024년 4월 14일

고분자화학

목록 보기

6/27

Thermodyanmic Systems

대부분의 step polymerization은 평형 반응이다. 그런데 열역학적 관점에서 thermodynamic system은 외부와의 에너지와 물질 교환 유무에 따라 3가지로 나눌 수 있다.

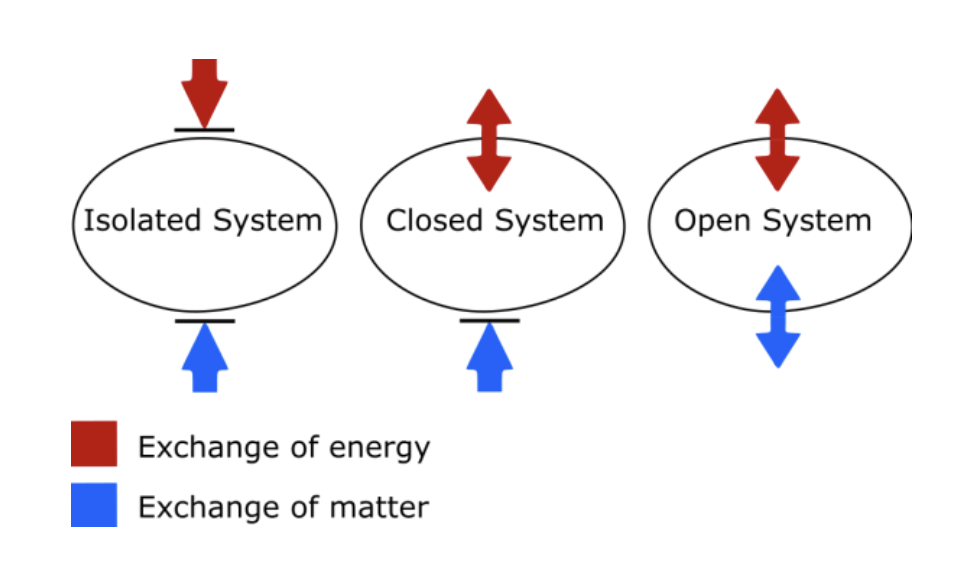
우선, 외부와 반응이 이루어지는 계 사이에서 어떠한 에너지와 물질의 교환도 없는 경우를 고립계(Isolated System)이라 하고, 만약 에너지의 교환은 존재한다면, 닫힌계(Closed System), 물질의 교환까지 자유롭게 이루어진다면, 열린계(Open System)이라고 한다.

Step Polymerization in Closed Systems

그렇기에 가장 먼저 고려해야 할 사항은 평행 상태에서 이루어지는 중합 반응들이 cloesd system에서 수행되는 경우 높은 분자량의 고분자를 생성할 수 있는지이다. closed system에서의 중합 반응은 순방향 반응의 생성물이 제거되지 않는 시스템을 의미한다. 물질의 교환이 이루어지지 않기 때문이다. 반응 계의 평형점을 고분자의 형성 쪽으로 밀거나 가속화 하는 어떠한 작업도 수행되지 않는다. 이러한 조건에서는 역반응 속도가 중합 속도와 같아질 때까지 생성물(중합체 및 일반적으로 물과 같은 작은 분자)의 농도가 축적된다. 즉, polyesterification 반응에서 $H_2O$ 를 지속적으로 제거했지만, 닫힌 계의 경우에는 불가능하다는 의미이다. 역반응은 일반적으로 해중합 반응이라고 하며, 고분자의 분자량은 평형이 성립되었을 때, 순방향 반응이 어느 정도 진행되었는지에 따라 결정된다. 외부 촉매 polyesterfication으로 예를 들어보자.

화학양론적 동몰을 가정한 경우, 두 반응기의 농도는 동일하기 때문에, 두 반응기의 초기 농도를 $[M]_0$ 으로 표시할 수 있다. 그리고 평형 상태에 도달했을 때의 반응 진척도(전환률)을 $p_e$ 로 새로 정의하면, 평형 상태에 도달했을 때 ester group의 농도는 $p_e[M]_0$ 라 표현할 수 있고, 반응 비가 $H_2O$ 도 동일하기 때문에, $H_2O$ 의 농도도 $p_e[M]_0$ 라 표현할 수 있다. 그럼 평형 상태에 도달했을 때, 두 반응기의 농도는

[M] = [M]_0 - [M]_0p_e = [M]_0(1-p_e)

가 된다. 닫힌 계의 polyesterification의 평형 상수( $K$ )는 어떻게 될까?

K = \frac{[\text{-COO-}][\text{H}_2\text{O}]}{[\text{COOH}][\text{OH}]} = \frac{p_e[M]_0 \times p_e[M]_0}{[M]_0(1-p_e) \times [M]_0(1-p_e)}=\frac{p_e^2}{(1-p_e)^2}

이제 Carother equation을 사용하여 평형 상태의 전환률 $p_e$ 를 수평균 중합도로 나타내보자. 그러기 위해, 평형 상수식을 $p_e$ 에 대해 정리하자.

\begin{aligned} \frac{p_e}{(1-p_e)} &= K^{1/2}\\ p_e &= K^{1/2}(1-p_e)\\ p_e + K^{1/2}p_e &= K^{1/2}\\ \therefore p_e &= \frac{K^{1/2}}{(1+K^{1/2})} \end{aligned}

이제 수평균 중합도를 carother equation을 이용해 구해보자.

\begin{aligned} \bar{X}_n &= \frac{1}{1-p_e} \quad\text{at equilibrium}\\ &= \frac{1+K^{1/2}}{1+K^{1/2}-K^{1/2}}\\ &= 1+K^{1/2} \end{aligned}

Equilbrium Consideration at Closed System

위에서 유도한 수식에 의하면, 수평균 중합도는 평형상수 $K$ 에 대한 식으로 나타내진다는 것이다. 그럼 위의 표를 통해 무엇을 알 수 있을까? 우선 수평균 중합도( $\bar{X}_n$ )이 100이 되어야 고분자라 정의할 수 있었다. 위 표에 의하면 수평균 중합도가 100에 도달하기 위해서 평형 상수는 9801이나 되어야 한다. 즉, 거의 1만( $10^4$ )에 가까워저야 높은 분자량의 고분자를 얻을 수 있다는 의미이다. polyesterification 반응의 평형 상수 $K$ 값은 대략 1에서 10정도의 값을 가진다. transesterification 반응의 경우는 심지어 0.1에서 1정도의 평형 상수 값을 가지며, 꽤 높은 polyamidation 반응에서도 100~1000 사이의 값을 가진다. 이는 즉, closed system에서는 높은 분자량의 고분자를 step polymerization으로 얻을 수 없다는 의미이다. 그 이유는 앞에서도 설명했고, 예전에 배운 polyesterification의 kinetics를 고려할 때, 부산물(by-product)인 $H_2O$ 를 지속적으로 제거해줌으로 반응 속도가 높아져, 높은 분자량의 고분자를 얻을 수 있는 step polymerization이 진행되었지만, 부산물의 제거가 없다면 해중합(역반응)이 정방향 반응과 동일한 속도로 진행되기 때문에 높은 분자량의 고분자를 얻기 힘들어지는 것이다.

Step Polymerization in Open Systems

그렇기에 대부분의 step polymerization은 open system에서 이루어진다. open system은 물질의 교환이 가능하기 때문에, 정방향(중합) 반응의 생성물 중 하나 이상을 제거하여 높은 분자량의 고분자가 생성되도록 평형을 유도해야 한다. 일반적으로 중합체보다는 저분자 부산물을 제거하는 것이 더 편리할 것이다. polyesterification의 경우, 물( $H_2O$ )이 저분자 부산물에 해당한다. 이를 제거하기 위해 반응 계의 온도를 끓는 점에 가깝게 높이는 것이 가장 간단한 방법일 것이다. 그 외에도 염산( $\text{HCl}$ )이 저분자 부산물이 되는 경우는 염기를 이용하여 중화시켜 제거하는 방법이 가장 효과적이다. 그러나 실제로 이렇게 고분자쪽으로 평형 반응을 움직이게 하는 것은 간단하지가 않다. 부산물이 제거되기 위해서는 반응 혼합물 안에서 부산물이 확산(diffusion)되어야 쉽게 제거될 수 있을 것이다. 하지만, 중합도가 높아지면서 고분자의 높은 분자량으로 인해 반응 혼합물은 용액 상의 점도가 상당히 높아진다. 결국, open system에서 중합은 저분자 부산물의 확산 속도에 의해 중합이 제어되는 확산 제어 중합(diffusion controlled)이 된다.

The extent to which one must drive the system in the forward direction can be seen by calculating the lowering of the small molecule concentration, which is necessary to achieve a particular molecular weight

특정 분자량을 달성하는 데 필요한 저분자 농도의 저하를 계산하여 시스템을 정방향으로 구동해야 하는 정도를 확인해야 한다는 의미이다.

Lowering small Molecule Concentration

동일하게 외부 촉매 polyesterification으로 예를 들어 알아보자. closed system이 아니기에 평형 상태에 도달한 경우가 아니기에 이 때의 전환률 $p$ 는 $p_e$ 가 아님에 주의하자.

그 외에 반응기가 있는 monomer의 초기 농도, 시간이 지나며 전환률에 의해 줄어든 monomer의 농도는 모두 동일하지만, 생성물 중 $H_2O$ 의 농도는 $p[M]_0$ 가 되지 않는다. 그 이유는 우리가 위에서 diffusion-controlled 중합을 하기 위해, small molecule 부산물의 농도를 낮춰 고정하기로 했기 때문이다. 그럼 평형 상수 $K$ 식은 다음과 같다.

\begin{aligned} K = \frac{[\text{-COO-}][\text{H}_2\text{O}]}{[\text{COOH}][\text{OH}]} &= \frac{p[M]_0 \times [\text{H}_2\text{O}]}{[M]_0(1-p) \times [M]_0(1-p)}\\ &=\frac{p[\text{H}_2\text{O}]}{[M]_0(1-p)^2} \end{aligned}

여기서 Carother equation을 이용하면,

K = \frac{p[\text{H}_2\text{O}]\bar{X}_n^2}{[M]_0}

로 정리할 수 있다. 우리가 계산해야 하는 것은 "특정(높은) 분자량에 도달하기 위해 필요한 저분자의 농도"이므로 $[\text{H}_2\text{O}]$ 에 해당한다. 그렇기에 위 식을 $[\text{H}_2\text{O}]$ 에 대해 정리하면,

[\text{H}_2\text{O}] = \frac{K[M]_0}{\bar{X}_n(\bar{X}_n-1)}

즉, 저분자의 농도는 monomer의 초기 농도에 비례하고, 수평균 중합도에 반비례 한다는 것을 알 수 있다. 그렇다면, open system에서 높은 $\bar{X}_n$ 값을 얻기 위해 상당히 작은 $[\text{H}_2\text{O}]$ 값이 필요하다고 결론지을 수 있다. 아래의 표를 확인해보자.

높은 분자량을 가진 고분자에 도달하기 위해, $[\text{H}_2\text{O}]$ 를 낮춰야 하는 양은 유리한 평형 상태( $K$ 값이 클수록)일수록 더 적다. 이 의미는 무작정 $[\text{H}_2\text{O}]$ 를 낮추기보단, 어느 정도의 큰 $K$ 값에서 $\bar{X}_n=100$ 이 되도록 $[\text{H}_2\text{O}]$ 의 농도를 낮춰야 한다는 의미이다. 실제로 물의 농도가 $10^{-5}$ 에 도달하게 하는 것은 상당히 힘들기 때문이다. 예를 들어 polyamide의 합성에서 평형 상수는 100보다 큰 값을 갖는다. 하지만 polyesterification의 경우에는 위에서 설명했듯, 그보다 훨씬 작은 값을 갖게 되는데, 이는 polyamidation 반응에서 낮추는 물의 농도보다 polyesterification 반응에서 낮추는 물의 농도가 훨씬 크다는 것을 의미한다.

jmt

고분자/컴공

이전 포스트

[고분자화학] 2-3 Accessibility of Functional Group

다음 포스트

[고분자화학] 2-4 Equilibrium Considerations