Stoichiometric Control

step polymerization에서 중합을 거쳐 우리가 원하는 분자량에 도달하는 고분자를 만들었다면, 어떻게 반응을 종료시킬까? Carother equation에 의해 수평균 중합도는 시간에 따른 함수이기에, 우리는 일정 시간 뒤 특정 수평균 중합도에 도달하면 반응을 중단시켜야 하는데, 이 때 Quenching을 한다. 온도를 낮추어 계의 반응을 중단시키는 것이다. 하지만 이 방법에는 단점이 있는데, Quencing을 통해 얻어진 고분자는 불안정하다는 것이다. 그 이유는 고분자의 양 단에 functional group은 여전히 반응성을 가진 채 존재하고 있는데, 전체 계의 온도를 급격히 낮추어도 예상치 못한 변수로 열이 발생하면, 살아있는 functioanl group이 다른 monomer와 반응하여 원치 않는 $\bar{X}_n$의 고분자를 얻게 될 수 있기 때문이다. 이 상황을 해결하기 위해, 두 개의 monomer의 농도를 조절한다. 화학 시간에 배운 한계 반응물의 개념처럼, monomer 중 하나의 농도를 더 적게 혹은 다른 하나를 더 많이 계에 투입한다면, 농도가 부족한 monomer는 중합 과정에서 더 이상 반응할 monomer가 없기에, 더 이상의 중합 반응이 일어나지 않게 되고 우리가 원하는 $\bar{X}_n$의 고분자를 얻을 수 있게 된다. 즉 약간 비동몰(slightly nonstoichiometric)의 monomer로 step polymerization을 수행하는 것이다.

Polyamide step polymerization

diamine과 diacid를 반응시켜 만드는 polyamide의 step polymerization을 예시로 stoichiometric control을 알아보자. 두 반응물 중 하나를 과량으로 설정해보자.

Excess Diamine

diamine이 과량이라면, 다음과 같은 반응이 이루어질 것이다.

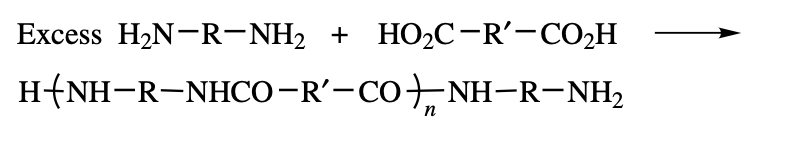
생성된 고분자는 diacid가 부족하여, 더 이상 중합되지 못하고 양 끝이 amine group을 가진 polyamide가 생성된다.

Excess Diacid

diacid가 과량이라면, 다음과 같은 반응이 이루어질 것이다.

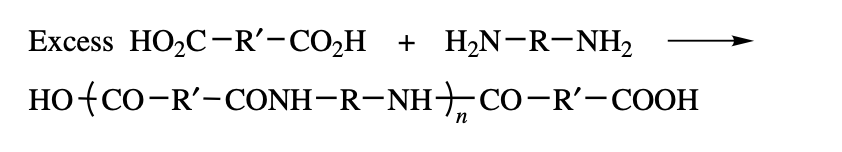
생성된 고분자는 diamine이 부족하여, 더 이상 중합되지 못하고 양 끝이 caboxyl group을 가진 polyamide가 생성된다.

Addition Chain Stopper

두 반응물 중 하나를 과량으로 두는 것 외에도 monofunctional group을 가지는 monomer를 소량 반응 계에 넣게 된다면, 성장하는 chain의 양 끝에 bifunctional group이 붙는 것이 아닌 monofunctional group이 붙어 더 이상 중합 반응이 일어나지 않게 할 수 있다. 여기서 사용되는 chain stopper는 acetic acid, lauric acid, benzoic acid 등이 사용된다. 반응은 다음과 같다.

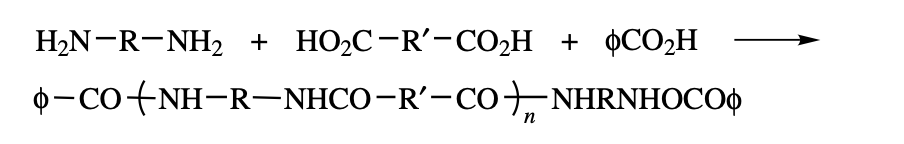
Quantitative Aspects

이제 수식으로 어떻게 표현되고 화학양론을 조절하는 것으로 수평균 중합도가 어떻게 되는지를 알아보자.

위와 같은 형태의 2개의 monomer가 있다 가정하자. 둘 중에 $\text{B}-\text{R}^{\prime}-\text{B}$과 과량(excess)로 존재한다고 가정하자. step polymerization에서 전환률에 따른 수평균 중합도를 알아보기 위해 다음과 같은 변수들을 설정할 수 있다.

여기서 주의해야할 점은 stoichiometric ratio, $r$값은 $r<1$여야 한다는 것이다. 동몰일 경우 $r=1$이 되어야한다. 전환률(extent of reaction, =conversion)은 특정 시간 $t$에서 먼저 소진되는 limiting group을 기준으로 계산한다. 위의 예시에서는 B가 과량이기에, A를 기준으로 설정할 수 있다. 그리고 특정 시간 $t$에서 반응하지 않은 A 그룹의 수와 B 그룹의 수는 $p$를 이용하여 다음과 같이 구할 수 있다.

그럼 수평균 중합도 $\bar{X}_n$의 정의에 의해 다음과 같이 구해진다.

즉, step polymerization에서 동몰이 아닌 경우, stoichiometric ratio $r$값과 extent of reaction $p$값에 의해 달라진다는 것을 알 수 있다.

Stoichiometric Amounts

동몰인 경우에 $r=1$이 될 것이다. 그럼 수평균 중합도는

가 되고, 결국 Carother equation과 동일하다는 것을 확인할 수 있다. 그 이유는 Carother equation에서 중합으로 생성되는 고분자는 linear polymer라고 가정했고, 이를 위해 몇 가지의 가정이 추가되었는데, 그 때 반응하는 두 개의 monomer는 동일한 양이여야 했다. 즉, 동몰($r=1$)이라는 소리다. 그렇기에 stoichiometric control을 가정하여도, 동몰인 경우 수평균 중합도는 Carother equation과 동일하다.

100% Conversion

전환률이 100%라면 conversion $p$값이 1이다. $p=1$이라면 위에서 유도한 수평균 중합도 $\bar{X}_n$은 다음과 같다.

물론, 전환률이 1이라는 것은 이론상 중합의 최대 시간이 흘렀다는 것을 가정한 것이다. 이것이 어떤 영향을 끼치는지 알아보자. 만약, A의 농도가 48, B의 농도가 50 정도라고 가정했을 때, $r$값은 $48/50=96/100=0.96$이다. 위 식에 그대로 대입하면,

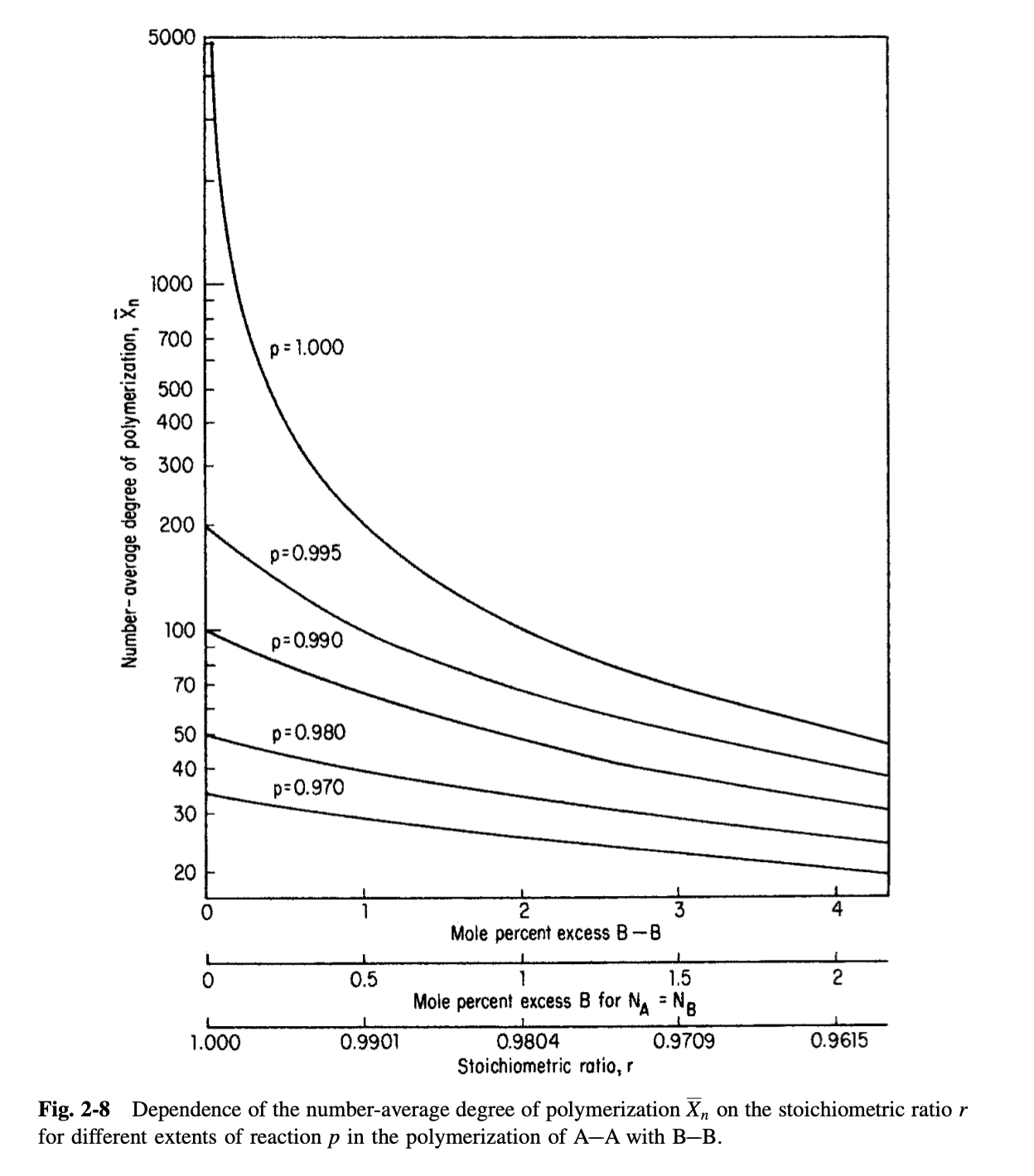
만약, A와 B의 농도가 모두 50정도라면, 전환률이 1이 아닌 그보다 작은 값 $p=0.99$여도 $\bar{X}_n = 100$에 도달한다. 상당한 차이가 존재함을 확인할 수 있다. 결론적으로 $r, p$값에 따라 수평균 중합도가 달라진다는 것인데, 이를 실험으로 plot한 그래프는 아래와 같다.