Introduction

그래프를 표현하는 방법과 그래프를 검색하는 방법에 대해 알아보자. 그래프를 검색한다는 것은 그래프의 모든 정점을 방문하는 것으로, 효율적으로 방문하기 위한 지나가야하는 간선을 찾아야한다. 그래프를 표현하는 가장 일반적인 2가지 방법은 인접 리스트와 인접 행렬이 있고, 그래프 탐색 방법에는 너비 우선 탐색(BFS)와 깊이 우선 탐색(DFS)가 있다. DFS의 응용으로 방향 비순환 그래프의 위상 정렬(topological sort)과 방향 그래프의 강한 결합 요소(strongly connected components)를 찾는 알고리즘도 알아보자.

그래프의 표현

일부 object의 set이 관련이 있는 자료 구조를 그래프라고 한다. 이 때 vertex(정점, 혹은 node라고 한다.)는 object를 표현한 것이고, vertex를 이은 edge로 관련이 있는 object를 이은 형태를 가진다.

인접 리스트(Adjacency List)

인접 리스트는 $|V|$개 리스트의 배열 $Adj$로 구성되어 있고 여기서 각 리스트는 $V$에 들어 있는 정점 하나에 대한 것이다. 각 $u \in V$에 대해 인접 리스트 $Adj[u]$는 간선 $(u, v) \in E$가 존재하는 모든 정점 $v$를 포함한다. 말이 좀 복잡한데, $Adj[u]$는 그래프 $G$의 정점 $u$에 인접해 있는 모든 정점($v$)로 구성된다.

그렇기에 방향 그래프라면 인접 리스트의 길이의 총 합은 $|E|$가 되고, 무방향 그래프라면 간선 $(u, v)$는 $u$와 $V$의 인접 리스트에 모두 표현되므로 인접 리스트의 길이의 총 합은 $2|E|$가 된다. 방향 그래프, 무방향 그래프 모두에 필요한 메모리의 양이 $\Theta(V + E)$가 되는 것이다. 여기서 가중치 그래프를 표현한다면 어떻게 될까?

가중치가 다음과 같이 표현된다고 하자.

$R$이라는 것은 여기서 실수를 의미한다. 그래프 $G = (V, E)$가 위에서 표현된 가중치 함수 $w$를 가진 그래프라고 하자. 간선 $(u, v) \in E$의 가중치 $w(u, v)$는 정점 $v$와 함께 정점 $u$의 인접 리스트에 쉽게 저장될 수 있다.

인접 리스트는 메모리 측면에서 상당히 효율적인 면을 보이지만, 주어진 간선 $(u, v)$가 그래프에 있는지를 확인하기 위해 인접 리스트 $Adj[u]$에서 $v$를 검색하는 것보다 빠른 방법을 제공하지 못한다는 것이다. $u$에 대한 모든 인접 정점을 탐색하는 시간은 $\Theta(degree(u))$가 될 것이고 그렇기에 간선 $(u, v)$를 탐색하는 시간은 $O(degree(u))$가 된다.

인접 행렬(Adjacency Matrix)

인접 행렬은 그래프 $G$를 $|V| \times |V|$ 크기의 행렬(matrix) $A$로 표현하는 방법이다. 이때 각 정점은 임의의 순서로 번호(1부터 |V|까지)가 매겨져 있다고 가정한다. 행렬의 각 요소의 값으로 그래프의 정점이 간선으로 이어져 있는지 구분한다. 식으로 표현하면 다음과 같다.

인접 리스트가 메모리 측면에서 효율적인 면을 보인 반면 인접 행렬은 비효율적인 메모리 운용을 보인다. 인접 행렬은 방향 그래프, 무방향 그래프에 무관하게 $\Theta(V^2)$의 메모리를 차지하게 된다. 메모리와 시간(복잡도)의 trade-off 관계를 생각해보자. 인접 행렬은 어떤 간선을 탐색하는데 당연히 매우 빠를 것이다. 정점을 임의의 번호로 매겨 2차원 행렬로 표현되어 있기 때문에, 탐색하는 시간은 $\Theta(1)$이다. 무방향 그래프를 인접 행렬로 표현하면 주대각선에 따라 대칭이 된다. 그렇기에 $A = A^T$의 관계가 성립하므로 무방향 그래프의 경우 대각선과 그 위 혹은 아래 원소만 저장하게 하여 필요한 메모리를 약 절반으로 줄이는 방법도 가능할 것이다. 가중치 그래프를 인접 행렬로 표현하게 되면 행렬의 각 원소에 가중치 $w(u, v)$에 해당하는 값이 들어가게 될 것이다. 간선이 없는 경우는 주로 $0$ 혹은 $\infin$을 통해 표현한다.

인접 리스트가 메모리 측면에서 효율적이지만 표현법은 인접 행렬이 더 간단하기에, 정점의 개수 $|V|$가 작은 경우에는 인접 행렬 방법이 더 좋을 것이다. 또한 가중치가 없는 그래프에 대해 인접 행렬은 행렬 원소마다 한 비트만 필요하다는 장점도 있다.

그래프 탐색

너비 우선 탐색(Breadth-First Search)

BFS는 가장 간단한 그래프 검색 알고리즘으로 프림의 최소 신장 트리 알고리즘과 다익스트라의 단일 출발점 최단 경로 알고리즘의 원형이 된다. BFS의 input은 2개가 있다. 가장 먼저 그래프 $G = (V, E)$가 있을 것이고, 출발점(source) $s \in V$가 있어야 한다. 출발점 $s$로 부터 도달할 수 있는 모든 정점을 발견하기 위해 $G$의 간선을 체계적으로 탐색한다. BFS는 너비 우선 탐색 방법이기에, 도달할 수 있는 정점을 발견할 때, $s$로부터 도달할 수 있는 각 정점까지의 거리를 계산한다. 그렇기에 output으로 $v.d \in \text{distance}$와 $v.\pi$가 주어진다. $v.d$는 $s$에서 $v$까지의 거리로 가장 적은 edge의 수를 의미한다. 그리고 $v.\pi$는 $s$에서 $v$의 가장 짧은 path(shortest path)에서 가장 마지막 edge를 의미한다. 이때 $v.\pi$가 $(u, v)$이면 $u$가 $v$의 직전 원소 또는 부모(predecessor)라 한다. BFS의 idea는 FIFO의 특징을 가지는 큐(queue) $Q$를 이용하여 구현한다. $s$에서 가장 짧은 거리(1)로 찾을 수 있는 모든 정점을 먼저 Q에 넣고, 그 다음 거리가 2인 모든 정점을 Q에 넣고 이를 계속 반복한다.

우선 line 1~4 수도 코드를 보면 알 수 있듯이, $s$를 제외하고 모든 정점을 흰색으로 칠하고, $u.d, u.\pi$는 각각 무한대와 NIL로 설정한다. 아직 탐색전이기 때문이다. line 5를 보면, $s$를 회색으로 칠하고(현재 탐색 중) $s.d, s.\pi$를 0과 NIL로 설정한다. 그 후 비어있는 큐인 Q를 만들고, Q에 s를 집어넣는다. 그 뒤, line 10~18까지 while 반복문을 돌면서 회색 정점이 남아 있는 동안 반복된다. 이때 while 반복문이 도는 동안 큐 Q는 회색 정점으로 구성된다. line 13의 if문을 통해 정점이 흰색이면 아직 발견된 것이 아니므로 line 14~17을 수행하고, 검은색으로 설정해 방문한 것으로 설정한다.

깊이 우선 탐색(Depth-First Search)

DFS는 그래프에서 가능한 깊게 탐색하는 방법이다. 가장 최근 발견한 vertex의 아직 방문하지 않은 edge를 따라가 탐색하는 방식이다. 만약 임의의 정점 $v$의 edge를 모드 탐색했다면, 역추적(backtrack)하여 정점 $v$를 떠나는 edge를 탐색한다. 이 과정은 source vertex에서 도달 가능한 모든 vertex들을 탐색할 때까지 반복한다. 만약 발견되지 않은 정점이 남아 있으면, BFS는 그 중 하나를 새 source로 선택하고 해당 source에서 검색을 반복한다.

DFS에 대한 input으로는 그래프 $G = (V, E)$가 주어진다. 이때 그래프는 방향 그래프 / 무방향 그래프 둘 다 가능하며, source vertex는 주어질 필요가 없다. output으로는 모든 vertex에 대한 2개의 timestamps가 존재한다. $v.d$는 discovery time으로 발견된 시점이고, $v.f$는 finishing time으로 탐색이 끝나는 시간이다. $v.\pi$는 vertex $v$의 직전 원소(predecessor)가 된다. DFS도 진행되면서 vertex에 칠해지는 색깔이 존재한다.

• WHITE = undiscovered
• GRAY = discovered, but not finished
• BLACK = finished
  

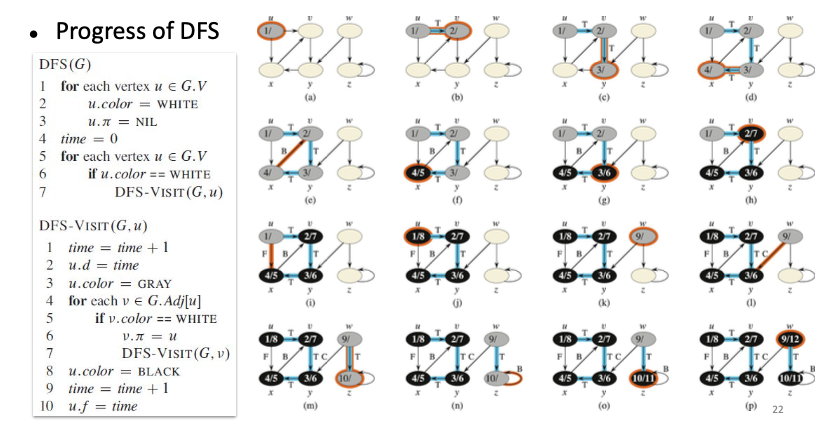
DFS의 수도 코드 line 1~4을 보면 그래프 $G$의 모든 vertex들에 대해 WHITE로 칠하고, $v.\pi = \text{NIL}$로 설정한다. 그래고 discovery time / finshing time을 작성하기 위한 time을 0으로 설정한다. 그 뒤 line 5~7을 따라 그래프의 모든 vertex에 대해 반복문을 돌며, WHITE(아직 발견되지 않은) 정점인 경우 $\text{DFS-VISIT}(G, u)$ 함수를 호출한다. $\text{DFS-VISIT}$ 함수는 line 1~3에 따라 호출되자마자 바로 time + 1로 설정한 뒤, $u.d$, discovery time을 time으로 설정한다. 발견 시점을 기록하는 것이다. 그 뒤 color를 GRAY로 설정하여 탐색 중임을 표시한다. 그 뒤 line4~7을 따라 $G.Adj[u]$, $u$의 인접 리스트에 속하는 모든 간선에 대해 WHITE라면(아직 발견되지 않은 경우), $v.\pi = u$로 설정하고, $\text{DFS-VISIT}$을 재귀호출한다. 모든 인접리스트를 돌며 vertex $u$에 대한 탐색이 종료되면, BLACK으로 color를 설정하여 탐색이 종료되었음을 표시하고, time에 다시 +1을 더한 뒤 $u.f = time$으로 설정하여 finshing time을 기록한다.

BFS보다 더 간단한 구조로, 모든 vertex를 탐색하는데 걸리는 시간은 $\Theta(V + E)$이다. $\text{DFS}(G)$의 코드를 돌면서 line1~3과 5~7의 반복문에 의해 $\Theta(V)$의 시간이 소모될 것이고, $\text{DFS-VISIT}$의 코드의 line4~7의 반복문에 의해 $\Theta(E)$의 시간이 소모될 것이다. 그러므로 탐색에 걸리는 총 시간은 $\Theta(V+E)$가 된다.

DFS의 특성

Depth-First Forest

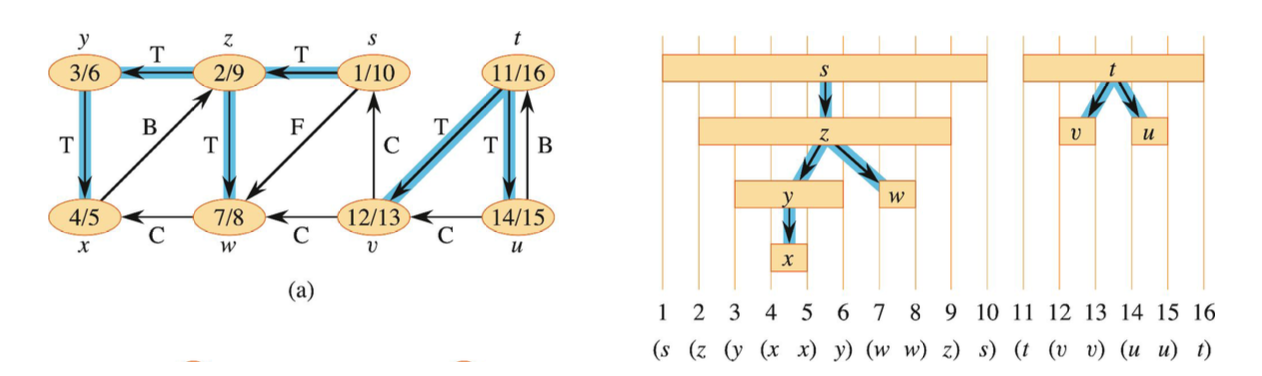
DFS를 통해 depth-first forest를 형성할 수 있다. 이는 depth-first trees로 구성된 더 큰 tree로 보면 된다. 각 tree는 edge $(u, v)$로 구성되어 있고, 여기서 $u, v$는 $u$가 GRAY이고 $v$가 WHITE인 edge를 의미한다. tree를 구분하는 방법은 discovery time과 finsihing time을 통해 괄호 구조(parenthesis structure)를 형성할 수 있다.

Classification of edges

Parenthesis Theorem에 의해 그래프의 vertex의 time stamps를 이용하여 두 vertex $u, v$의 자손 관계를 판단할 수 있다.

모든 u와 v 정점은 다음의 조건중 하나에 만족한다.
1. d[u] < f[u] < d[v] < f[v] 또는 d[v] < f[v] < d[u] < f[u]
따라서, u와 v는 Descendant(자손)관계가 성립하지 않는다.
2. d[u] < d[v] < f[v] < d[u]
따라서, v는 u의 Descendant(자손)이다.
3. d[v] < d[u] < f[u] < d[v]
따라서, u는 v의 Descendant(자손)이다.

또한 DFS를 통해 edge의 분류도 가능하다. 우선, DFS를 통해 탐색된 edge들은 모두 tree edge(T)라고 불린다. back edge(B)는 edge $(u, v)$에 대해 $u$가 $v$의 자손인 경우를 가리킨다. forward edge(F)는 $v$가 $u$의 자손인 edge $(u, v)$를 의미한다. 단, 여기에 추가적인 조건이 붙는데, DFS로 탐색되지 않은, 즉 tree edge가 아니여야 한다. 마지막으로 cross edge(C)는 위의 T, B, F에 속하지 않은 edge를 의미한다. 동일한 depth-first tree에 있는 vertices와 다른 depth-first tree에 있는 vertices를 연결하는 edge가 될 것이다.