Applications of DFS

Topological Sort

사이클이 존재하지 않는 방향 그래프의 위상정렬을 수행하기 위해 DFS가 사용된다. 사이클이 존재하지 않는 방향 그래프(directed acyclic graph)를 “dag”라고 하자. dag $G = (V, E)$의 위상 정렬은 그래프의 모든 vertex에 대한 선형적인 정렬이다. 위상 정렬은 여러 작업들이 있을 때 특정 작업을 수행하기 전 진행되어야 할 작업들이 있는 경우(예를 들어 선수과목 이수체계) 유용하다. 작업들을 순서에 맞게 정렬해주는 것을 위상 정렬이라 한다.

위와 같은 그래프가 있다고 하자. 위상 정렬의 수도 코드를 살펴보면, 우선 깊이 우선 탐색 DFS를 통해 그래프 $G$의 모든 vertex $v$ 의 finishing time인 $v.f$를 계산한다. 그 후 vertex의 탐색이 종료될 때마다, 연결 리스트의 가장 앞에 넣는다. 위 그래프에 DFS를 적용하면, 종료되는 순서의 역순은 socks, undershorts, pants, shoes, watch, shirt, belt, tie, jacket 순이다. 이 순서가 바로 위상 정렬의 return 값인 연결 리스트의 순서가 된다.

Strongly Connected Components

어떤 방향 그래프의 모든 vertices pair에 대해 서로가 서로를 가리키는 경로가 있는 경우, 강하게 연결된 그래프(Strongly Connected Components; SCC)라고 한다. 어떤 그래프 $G=(V, E)$의 SCC는 다음의 최대 집합이다.

그래프 $G$의 SCC를 찾는 알고리즘은 $G$의 전치 그래프를 사용한다. $G$의 전치 그래프는 $G^T$를 의미한다. 이는 수식으로 다음과 같다.

즉, 거꾸로 된 방향을 바꾼 $G$의 간선(edge)들로 구성된다. $G$의 전치 그래프를 이용해 SCC를 찾을 수 있는 이유는 $G$의 SCC와 $G^T$의 SCC는 동일하다. (명제의 대우를 생각하면 이유는 간단하다.) SCC를 구하는 수도 코드는 다음과 같다.

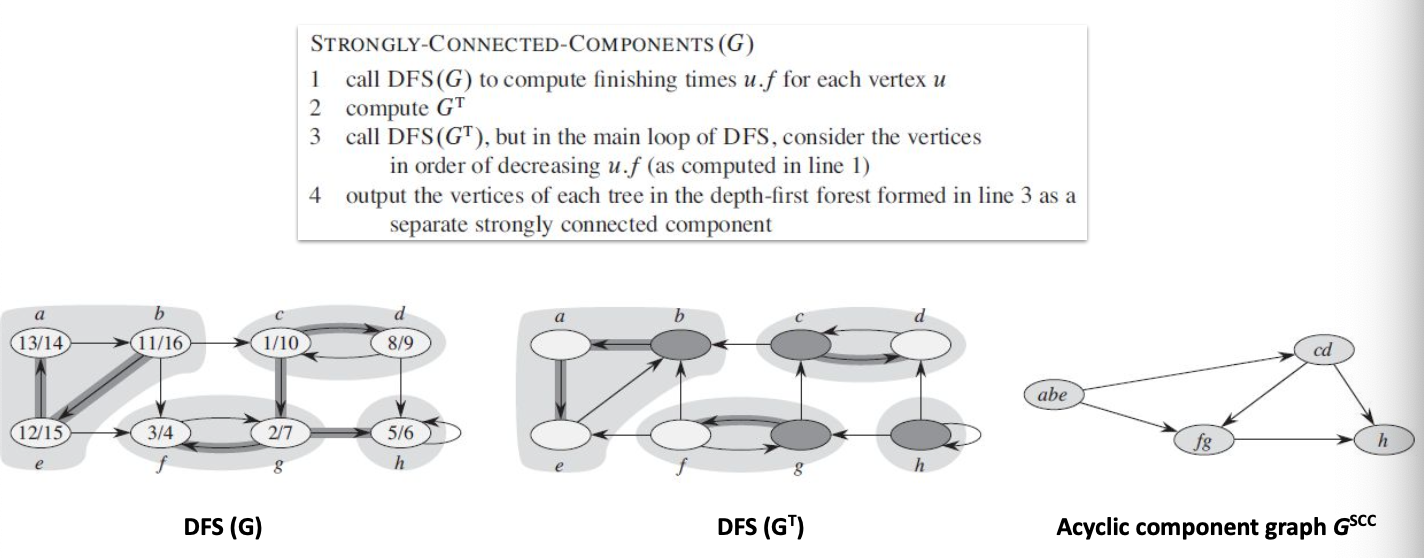
DFS($G$)를 수행하여 모든 vertex $u$의 $u.f$를 계산한다. 그리고 $G$의 모든 edge의 역방향 edge로 구성된 $G^T$를 계산한다. 그 다음 DFS($G^T$)를 수행하는데, 이 때 $u.f$가 큰 순서로, 즉 $u.f$가 감소하는 순서로 $G^T$의 DFS를 수행한다. 이를 통해 SCC를 구하는데, 위 그림의 그래프에 적용해보자.

DFS($G$)의 실행결과 수행 뒤, $u.f$가 감소하는 순서로 DFS($G^T$)를 수행해보자. 그럼, 가장 먼저 vertex $b$를 방문하게 된다. 그러면, $b\rightarrow a \rightarrow e$의 순서로 vertex를 방문하고, $e$에서 더 이상 방문할 수 있는 vertex가 없기 때문에, $abe$가 하나의 SCC가 된다. 그 다음 방문 vertex는 $c$가 된다. 마찬가지로 $c \rightarrow d$를 방문하게 되고 DFS가 종료되기에 $cd$가 하나의 SCC가 된다. 이를 계속 반복해나가면 위 그림의 3번째 그림인 비순환 요소 그래프, $G^{SCC}$가 된다.