Elements of Greedy Strategy

이전에 activity selection 문제를 풀기 위해 어떻게 풀었는지 복습해보자.
1. optimal substurcture를 찾는다.
2. recursive solution을 어떻게 구하는지 구한다.
3. 하나의 subproblem을 풀 때, greedy choice를 할 수 있는지 보인다.
4. greedy choice로 전체 문제의 최적해를 구할 수 있는지 보인다.
5. recursive greedy algorithm 으로 문제를 푼다.
6. 혹은 iterative algorithm으로 바꿔본다.

이를 통해 좀 더 greedy algorithm을 풀 수 있는 문제의 특징들을 알아보자.

Greedy Choice Property

Greedy algorithm으로 풀기 위해서는 최적해를 구하는 문제가 "그리디 선택 특성(greedy choice property)"와 optimal substructure를 갖고 있어야 한다. 그리디 선택 특성이 무엇인지 알아보자.

Greedy Choice Property : we can assemble a grlobally optimal solution by making locally optimal (greedy) choices. In other words, when we are considering which choice to make, we make the choice that looks best in the current problem, without considering results from subproblems.

즉, 부분적인 greedy choice, 현재 선택할 수 있는 것 중 가장 최선의 선택으로 전체적인 optimal solution이 되는 것을 그리디 선택 특성이라 한다.

DP vs Greedy

greedy alogrithm으로 풀 수 있는 문제의 또다른 특성은 optiaml substructure인데, 이는 DP 기법으로 풀 수 있는 문제가 가지는 공통적인 특징이다. 하지만, optimal substructure만 가진다고 greedy algorithm으로 풀 수 없는 문제도 있다. 이를 위해 Knapsack Problem을 예시로 알아보자.

0-1 Knapsack Problem

0-1 knapsack 문제의 경우에는 각각 가치 $v_i$를 가지고 무게 $w_i$를 갖는 $n$개의 item들이 존재할 때, 최대로 무게 $W$를 담을 수 있는 가방에 어떻게 물건들을 넣어야 가장 가치가 높은 지를 찾는 문제이다. 아래와 같은 예시가 있다고 하자.

만약, 이 문제를 greedy algorithm으로 풀려고 한다면, 무게 당 가치가 높은 물건들을 먼저 선택하는 greedy choice를 하게 된다. 무게 당 가치를 따로 계산하면, $v_i / w_i$가 될 것이다. 위 문제에서 무게 당 가치를 계산해보면, $\{6, 5, 4\}$가 될 것이다. 그리고 무게 당 가치가 높은 순서로 가방에 넣게 되면 $W=50$이므로, 가방에는 item 1과 item 2만 담아진다. 하지만 실제로 이것이 최적해일까? 그렇지 않다. 최적해는 item 2와 item 3을 가방에 담아, 가방에 남는 무게를 0으로 딱 맞춰서 총 가치 220을 담는 경우가 된다. greedy solution은 총 가치 160밖에 되지 못하고, 무게도 20이나 남는다. 이런 문제는 optimal substructure를 갖지만, greedy algorithm으로 풀 수 없기에 DP 기법을 활용해야 한다.

Fractional Knapsack Problem

하지만, 만약 0-1 Knapsack 문제에서 조건을 추가하자. 가방에 담는 물건들이 고체가 아니라 액체거나 가루처럼 물건의 일부 부분을 우리가 가방에 나눠서 담을 수 있다고 하자. 이 때는 greedy choice가 도움이 된다. 실제로 이 문제를 위의 0-1 knapsack 문제 때와 동일하게 무게 당 가치가 높은 물건을 선택하는 greedy choice를 하게 되면, greedy solution이 optimal soultion이 되는 아래와 같은 경우가 나온다.

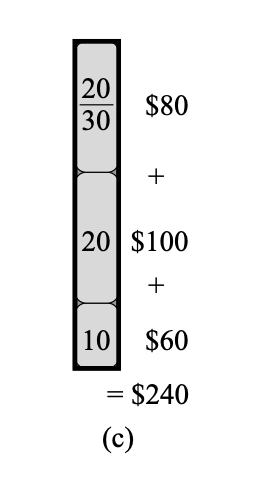
이를 증명해보자.

To show that "the fractional knapsack problem has greedy-choice property", suppose that some choice is not the greedy choice.

즉, 어떤 선택 중 하나가 greedy choice가 아니라고 가정하자. greedy choice는 $v_i / w_i$가 가장 높은 $\text{item}_m$을 고르는 것이라고 하자. 그런데 여기서 $\text{item}_m$을 고르지 않고, $\text{item}_q$를 골랐다고 하자. 무게 당 가치는 당연히 $\text{item}_q$가 더 낮다. 만약 $r= \min \{w_q, w_m \}$이라 하고, 이를 $\text{item}_q$를 $\text{item}_m$으로 바꾸는 양이라고 정의하자. greedy choice로 바꾼 경우, 가방의 전체 가치는 $r \times \frac{v_q}{w_q}$만큼 줄어들고 $r \times \frac{v_m}{w_m}$만큼 늘어난다. 이 때 $v_q/w_q < v_m/w_m$이 크기 때문에 전체 가치는 증가한다. 그러므로 greedy choice를 해야 optimal한 solution에 가까워질 수 있고, 이는 곧 그리디 선택 특성(greedy choice property)를 갖는다는 의미다!