Introduction

우리는 앞에서 최적화 문제(optimization problem) 알고리즘들을 배웠었다. 그 중 Greedy Technique를 배웠는데, 일련의 step을 진행하며, 각 step마다 greedy한 선택을 하며 문제를 해결하는 것이었다. 만약 greedy choice property(부분 문제에 대한 greedy choice로 전체 문제의 최적해를 구할 수 있다.)가 적용되지 않는 최적화 문제라면 dynamic programming으로 문제를 해결할 수도 있었다. 이는 부분 문제의 해를 기록(배열에 저장)하여 overlap되는 부분문제를 빠르게 해결하여 전체 문제의 최적해를 구하는 방법이였다. Greedy techinique은 여러 알고리즘에서 응용이 되는데 대표적으로 간단한 “scheduling problem”이 있었고, “knapsack problem”과 “Huffman code”도 다뤘다. 그래프 알고리즘에서는 최소 신장 트리(Minimum Spanning Tree; MST)를 구하는 알고리즘과 단일 성분 최단 거리(single-source shortest path)를 구하는 알고리즘에 적용된다. 이 중 MST에 대해 배워보자.

MST

최소 신장 트리는 무방향 그래프 $G$의 모든 vertex를 포함하는 tree이면서 비순환이여야 한다. 단, 모든 vertex를 연결할 때 각 edge마다 가중치 $w(u, v)$가 존재하는데, $w(T)=\sum_{(u, v)\in T} w(u, v)$가 최소인 트리를 최소 신장 트리, MST라고 한다. 최소 신장 트리는 “최소 가중치 신장 트리”라는 말의 단축형이고, 모든 spanning trees 중에서 가중치의 합이 최소인 spanning tree가 MST가 된다. MST의 특성으로는 다음이 있다.

• $|V|-1$ 개의 edge를 가진다
• cycle이 존재하지 않는다.
• 그래프 $G$에 대해 하나로 정해지지 않는다. 즉, unique 하지 않다.

아래 그림과 같이 파란색 edge들로 연결된 spanning tree가 바로 MST가 된다.

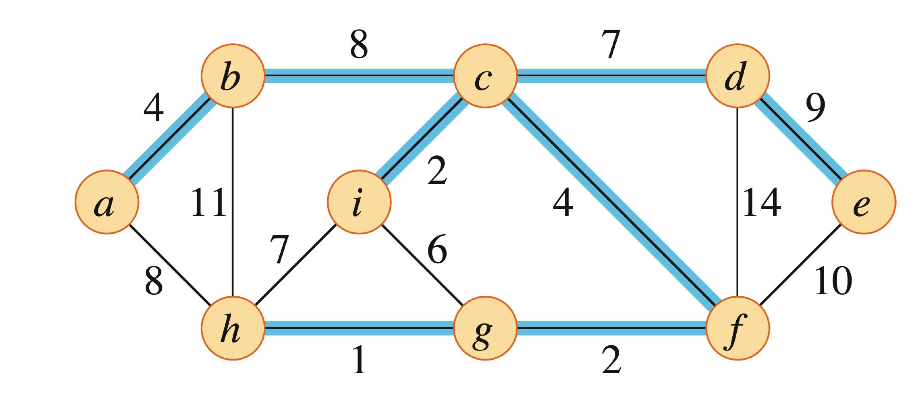
해당 MST의 가중치합은 37이다. edge $(b, c)$를 제거하고 $(a, h)$를 넣어도 MST가 되며 이는 MST의 not unique한 성질을 보여준다.

Generic MST

가중치 함수 $w:E \rightarrow \bf{R}$을 갖는 무방향 그래프 $G=(V, E)$가 있고, $G$의 최소 신장 트리를 찾는 방법 중 “일반적인(Generic)” 방법을 먼저 알아보자. 이 일반적인 방법은 우선 edge의 집합인 $A$를 이용한다. greedy 방법을 이용하여 반복문을 돌며 $A$에 edge를 추가해나간다. 각 단계마다 $A$는 MST의 부분 집합이 된다. 추가되는 edge가 $(u,v)$일 때, $A \cup \{(u, v)\}$도 MST의 부분 집합이 되도록하며 루프 불변성을 유지하게 한다. 루프 불변성을 유지하게끔 추가되는 edge를 안전 간선(safe edge)이라 한다. 유지되는 루프 불변성은 아래와 같을 것이다.

• initialization : empty set trivially satisfies the loop varient
• maintenance : since we add only safe edges, $A$ remains a subset of MST
• termination : all edges to $A$ are in an MST, so when we stop, $A$ is MST

이를 수도 코드로 작성하면 다음과 같다.

물론 수도 코드이기에 간단하지만, 실제 어떠한 알고리즘을 적용해야 하는 부분이 바로 line 3의 “find safe edge”이다. 안전 간선을 찾는 것은 다음과 같은 정리에 의해 얻어진다. 아래 정리를 이해하기 위해 절단(cut) 의 개념을 이해해야 한다. 무방향 그래프의 cut $(S, V-S)$는 $V$의 분할을 의미한다. 이때 어떤 edge $(u, v)$에서 $u$혹은 $v$가 $S$에 있고, 나머지는 $V-S$에 있다면, 해당 edge는 “cut을 교차(cross)한다” 라고 한다. 만약 $A$에 cut을 cross하는 edge가 없다면, cut은 edge의 집합인 $A$를 respect한다고 한다. 그리고 cut을 cross하는 edge들 중에 가중치가 최소인 edge를 경량 간선(light edge)라 한다.

$A$를 $G$의 MST에 포함되는 $E$의 부분 집합이라고 하자. 그리고 $(S, V-S)$는 $A$를 respect하는 $G$의 cut이고 $(u,v)$를 cut을 cross하는 light edge라고 하자. 그러면 $(u, v)$는 $A$에 대한 safe edge가 된다. 이 정리를 증명해보자. $T$가 $A$를 포함하는 MST라고 하자. 그리고 $T$에 $(u, v)$가 포함되지 않는다고 하자. 아래 그림에서 $(x, y)$를 제거하고 $(u, v)$를 $T$에 포함시켜서 $T^{\prime}$을 만들었다고 하자.

이 그림에서 서로 다른 색깔로 칠해진 vertex가 서로 $S$와 $V-S$에 속하는 vertex이고, 파란색으로 색칠된 edge가 $A$의 edge들이다.

$(u, v)$와 $(x, y)$ 모두 cut을 cross하는 edge지만, $(u,v)$가 light edge이므로, $T^{\prime}$은 MST가 될 것이다. 그 이유는 다음과 같다.

이제 $(u,v)$가 safe edge임을 보이자. $A \subseteq T$ 이고, $(x,y) \notin A$이므로 $A \subseteq T^{\prime}$이 성립한다. 따라서 $A \cup \{(u, v)\} \subseteq T^{\prime}$이 성립한다. 결과적으로 $T^{\prime}$은 MST이므로 $(u, v)$는 $A$에 대한 safe edge가 된다.

위와 같은 정리로 유도된 아래의 정리는 MST를 만드는 2개의 알고리즘에 이용된다.

간단하다. $G_A = (V, A)$에 있는 하나의 트리인 $C=(V_C, E_C)$가 있을 때, edge $(u,v)$가 $G_A$와 $C$를 cross하는 light edge라면, $(u,v)$는 $A$에 대한 safe edge이다. 이에 대한 증명도 간단하다. cut $(V_C, V-V_C)$ 는 $A$를 respect하고 $(u, v)$가 cut에 대한 light edge이므로, 위의 Theorem 23.1에 의해 $(u,v)$는 $A$에 대한 safe edge가 된다.

Kruskal’s Algorithm

Generic MST를 다듬은 알고리즘으로 safe edge를 찾기 위해 특정한 규칙이 하나 추가된 알고리즘이다. 크루스칼 알고리즘에서 집합 $A$는 포레스트(forest)로 $A$의 vertex는 주어진 그래프의 모든 vertex가 된다. 그리고 $A$에 더해지는 safe edge는 항상 그래프에서 두 개의 서로 다른 요소를 연결하고 최소 가중치를 가진다. 즉, 크루스칼 알고리즘은 각 단계에서 가장 가중치가 작은 edge를 forest에 추가하므로 그리디 알고리즘이다. 이는 따름 정리 Corollary 23.2에 의해 추가되는 edge가 safe edge임이 증명된다. ($A$가 forest이므로 $C_1, C_2$를 각각 forest를 구성하는 tree라고 보고 추가되는 edge가 $C_1, C_2$의 light edge이면 $A$의 saef edge가 된다.)

크루스칼 알고리즘의 구현은 서로 소인 여러 집합을 관리하기 위해 서로소 집합 자료구조(Disjoint Set) 를 사용한다. 각 집합은 forest의 트리 하나에 있는 vertex를 가지고, $\text{FIND-SET}(u)$는 $u$를 포함하는 집합에서 대표 원소를 return 한다. 그러므로 $\text{FIND-SET}(u)$와 $\text{FIND-SET}(v)$가 같은지 검사하여 두 vertex $u$와 $v$가 같은 트리에 속하는지 결정할 수 있다. 두 개의 트리를 하나로 만들기 위해 크루스칼 알고리즘은 $\text{UNION}$을 호출한다. 이를 구현한 소스코드와 동작 과정은 다음과 같다.

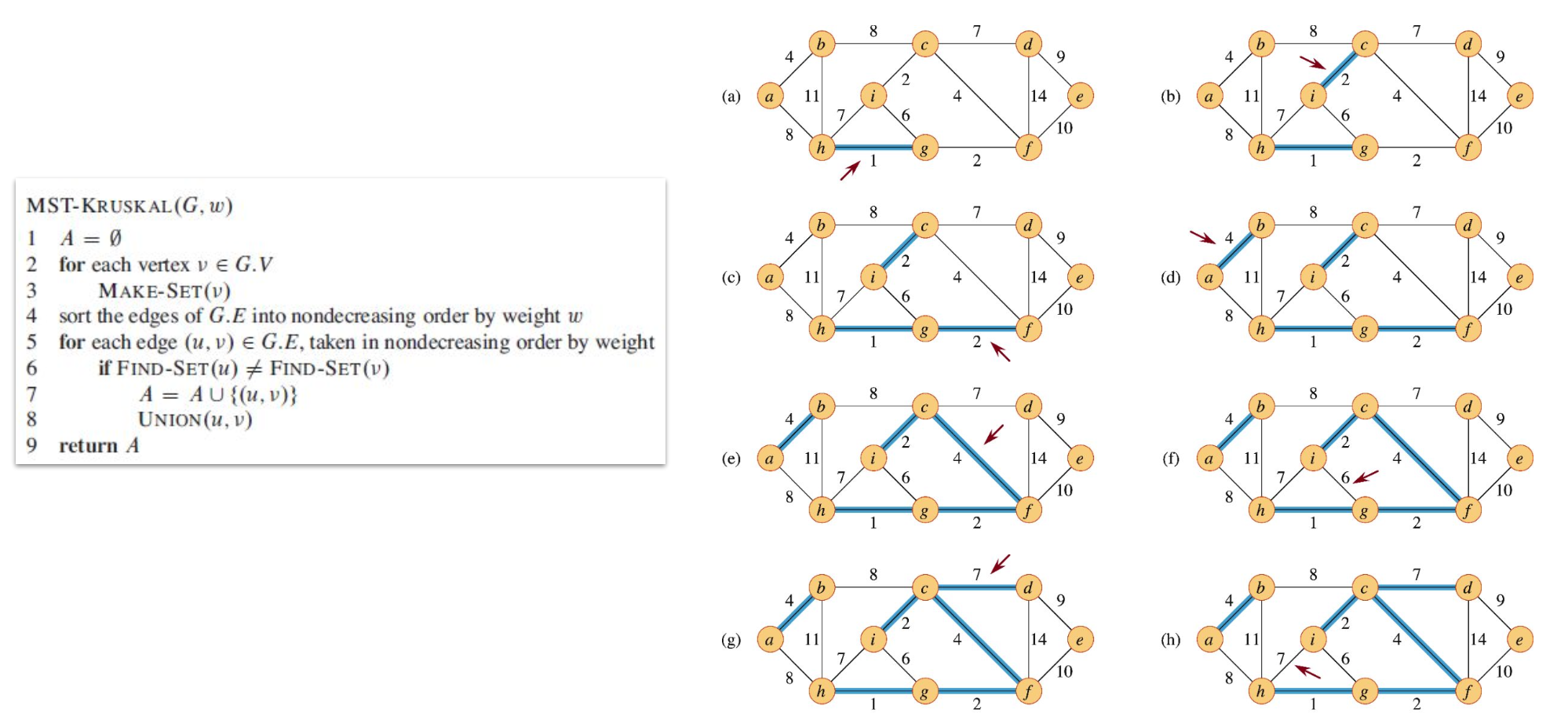
크루스칼 알고리즘은 그래프 $G$의 모든 vertex에 대한 집합(set)을 만든다. 그 후 모든 edge를 가중치 w에 대해 오름차순으로 정렬한다. 그리고 모든 edge$(u,v)$에 대해 $\text{FIND-SET}(u) \neq \text{FIND-SET}(v)$인지 확인한다. 이는 cycle이 형성되지 않기 위함이다. 해당 조건문을 통과하게 되면 앞에서 이야기한 정리들에 의해 edge$(u,v)$는 safe edge가 되고 $A$에 속하게 된다. 그리고 $\text{UNION}(u,v)$를 실행시켜 같은 집합으로 묶는다. 모든 edge를 탐색한 뒤 $A$를 리턴하면 해당 집합 $A$는 MST가 된다.

Prim's Algorithm

프림 알고리즘은 집합 $A$를 signle tree가 된다. 그리고 $A$에 추가되는 safe edge는 항상 트리에 없는 vertex와 signle tree인 $A$를 연결하는 최소 가중치를 갖는 edge가 된다. 즉, 프림 알고리즘 매 단계마다 가능한 최소값을 갖는 edge를 tree에 추가하는 선택하므로 greedy 알고리즘이라고 볼 수 있다. 프림 알고리즘은 크루스칼 알고리즘과 다르게 항상 single tree가 된다. 즉, root가 되는 $r$ node(vertex)가 필요하다. 그리고 매 단계마다 cut을 가로지는 light edge를 찾아야한다. 매 단계의 cut은 $(V_A, V-V_A)$가 될 것이다. 여기서 $V_A$는 $A$에 속하는 vertex로 구성된 집합이 된다. 그렇다면 프림 알고리즘에서 가장 중요한 것은 무엇일까? '어떻게 빠르게 light edge를 찾는가' 이다. 해결책으로 프림 알고리즘에서는 우선 순위 큐(priority queue)를 사용한다. 다음과 같은 수도 코드를 살펴보자.

우선 우선 순위 큐 $Q$에 속하는 요소들은 $V-V_A$에 속하는 vertex들이 된다. 그리고 vertex $v$의 속성으로 $key$는 모든 edge$(u,v),\text{ where }u\in V_A$의 가중치 중 최소값, 최소 가중치를 의미한다. 그리고 $\text{EXTRACT-MIN}(Q)$에 의해 vertex가 정해진다. 또한 만약 vertex $v$가 $V_A$에 있는 모든 vetex 중에 인접한 vertex가 없다면 $v.key = \infin$이 된다.

Kruskal vs Prim

두 알고리즘의 가장 큰 차이점은 크루스칼 알고리즘은 edge를 추가해나가며 MST를 확장해나간다. 하지만 프림 알고리즘은 vertex를 추가해나가며 MST를 확장해나간다. 크루스칼 알고리즘에서 가장 처음에 초기화하고 리턴되는 집합 $A$가 포레스트(forest)이기 때문이다. 그렇기에 edge를 탐색하기 위해 서로소 자료구조, disjoint set을 사용한다. 이는 보기에는 더 간단해보이지만, 구현이 좀 더 힘들다고 할 수 있다. 반면 프림 알고리즘은 리턴되는 집합 $A$는 동작 과정부터 리턴될 때까지 하나의 트리(tree)이다. 또한 구현에 사용되는 자료구조는 우선 순위 큐(priority queue)이다.

시간복잡도면에서는 크루스칼 알고리즘은 edge를 탐색하며 safe edge를 찾아 집합 $A$에 추가하기 때문에, $O(E \log E)$이다. 반면, 프림 알고리즘은 vertex를 탐색해나가며 우선 순위 큐를 사용하여 light edge를 찾아 기준이 되는 vertex와 light edge를 이루는 vertex를 연결한다. 그렇기에 $O (V \log E)$가 된다. 그렇기에 Dense Graph($V < E$)에서는 프림 알고리즘을 Sparse Graph($E < V$)에서는 크루스칼 알고리즘을 선택하는 것이 효율적일 것이다.