Introduction

shortest-paths problem은 지도 상에 두 지점 사이의 최단 거리를 찾는 문제이다. 이때 input으로는 방향 그래프(directed graph)와 가중치 함수(weight function)가 주어진다.

그리고 path와 path의 가중치를 계산하는 함수를 다음과 같이 정의하자.

그럼 vertex $u$에서 $v$로 가는 shortest-path weight는 다음과 같이 정의할 수 있다. 이때 기호 $\delta$를 사용한다.

또한 $u$에서 $v$로의 shortest path는 다음과 같이 정의된다.

여기서 생각해야할 shortest path의 특징은 unique하지 않다는 점이다. 또한 tree의 형태로 구성된다. 또한 Shortest Path Problem(이하 SPP은 다음과 같은 종류가 존재한다.

1. single-source SPP : 출발점(source)으로 주어진 $s$에서 $v \in V$의 모든 vertex를 지나가는 shortest path를 찾는 문제
2. single-destination SPP : 도착점(destination)으로 주어진 $d$로 도착하는 shortest path를 찾는 문제. 이는 single-source problem를 역순으로 푸는 것으로 reduce(환원)할 수 있다.
3. single-pair SPP : $u, v$의 vertex가 주어질 때 두 vertex를 지나가는 shortest path를 찾는 문제이다. single-source problem과 시간복잡도는 동일할 것이다.
4. all-pairs SPP : $u, v \in V$에 대한 모든 $u, v$의 shortest path를 찾는 문제이다.

Optimal Structure

예전에 기억하며 풀기라는 이름으로 불렀던 Dynammic Programming을 떠올려보자. 이때 optimal structure를 갖는다면 이전 연산에 사용되었던 값이 현재 step의 연산에 활용될 수 있었다. shortest path problem에도 적용이 가능한 지 확인해보자. 간단히 생각해보자. 만약 $v_0$에서 출발하여 $v_k$로 도착하는 어떤 shortest path $p$가 주어진다고 해보자. 만약 $v_0$과 $v_k$ 사이에 $v_i, v_j$라는 vertex가 존재한다면, shortest path $p$에 속하는 path 중 $v_0$에서 $v_i$로 가는 path, $p_{0i}$는 $v_0, v_i$에 대한 shortest path가 될 것이다. 물론 $v_i, v_j$에 대해서도 $v_0, v_j$에 대해서도 동일하게 적용된다. 즉, 이는 shortest path의 subpaths는 모두 shortest path가 된다는 의미이다. Introduction에서 정의한 기호로 작성하면 다음과 같다.

shortest path의 subpaths가 모두 shortest path인지 다음과 같이 증명해보자. 만약 $p_{ij}$보다 더 작은 shortest path가 존재한다고 해보자. 해당 path를 $p^{\prime}_{ij}$라고 쓰자.

전제가 $p$가 shortest path라고 했는데, subpaths가 바뀌니까 $w(p^{\prime}) < w(p)$가 되어버린다. 즉, $p^{\prime}$이 shortest path가 되므로 이는 모순이다.

Cycles

Negative-Weight Edges

특정 SPP를 해결하는 알고리즘은 가중치가 음수인 edge가 존재하지 않아야 정상적으로 작동한다. 결론부터 이야기하자면, 정상적으로 작동하는 경우는 source vertex에 연결된 edge들이 모두 음수인 가중치를 갖지 않는 경우이다. 물론 주어진 그래프에 shortest path를 찾다보면 이런 경우도 존재할 것이다. 그렇다면 정상적으로 작동하지 않는 경우는 언제일까? 바로 negative weight edges에 의해 cycle이 형성될 때이다. 만약 negative weight cycle이 존재하게 되면 해당 cycle을 순회하면서 점점 $w(s,v)$는 감소하게 되고 $-\infin$가 된다.

No Cycles!

shortest path는 cycle을 포함해서는 안된다. negative weight cycle을 갖는 경우는 위에서 설명했다. postive weight cycle의 경우에는 해당 cycle을 포함하게 되면 점점 $w(p)$가 증가할 것이기에 cycle을 제외함으로 더 shorter한 path를 찾을 수 있을 것이다. zero weight cycle의 경우에는 계속해서 제자리를 반복하기에 사용할 이유가 없다. 그렇기에 이러한 경우는 고려하지 않는다.

그럼 우리는 $|V|-1$의 edge를 갖는 shortest path에 대해서만 생각하면 된다. 그 이유는 주어진 그래프 $G=(V, E)$에 속하는 모든 비순환 경로(acyclic path)들은 $|V|$개의 vertex를 지나게 된다. 그러므로 shortest path에 포함되는 edge의 개수는 최대 $|V|-1$이다.

Represent Shortest Paths

Output of Algorithms

SPP의 output은 shortest path의 가중치만 주어저서는 안된다. shortest path에 포함되는 모든 vertices에 대한 정보도 있어야 한다. 그렇기에 다음과 같이 그래프 $G$에 속하는 모든 vertex, $v \in V$를 다음과 같이 정의하자.

$v.d$라는 값은 최초에는 $\infin$으로 초기화되겠지만, 알고리즘이 동작하면서 점차 값이 감소하게 될 것이다. 그리고 항상 $v.d \ge \delta(s,v)$를 만족해야한다. $v.\pi$는 predecessor이므로 존재하지 않는다면 $\text{NIL}$ 값을 갖게 될 것이다. 또한 $\pi$값을 통해 predecessor subgraph, $G_{\pi} = (V_{\pi}, E_{\pi})$를 유도할 수도 있을 것이다.

그리고 $G_\pi$는 shortest path tree가 된다.

Initialization

여태까지의 정의로 shortest path를 구하는 알고리즘을 수도코드로 표현해보자. $v \in G.V$의 모든 vertex에 대해 $v.d$ 값을 $\infin$으로 초기화하고, $v.\pi$는 $\text{NIL}$로 초기화한다. 그리고 source vertex인 $s.d = 0$으로 초기화한다.

Relaxation

shortext path를 찾기 위해 Relaxation을 진행한다. edge$(u, v)$를 relaxing하는 과정은 $u$에서 $v$로 가는 path들 중에 더 짧은 path가 있는 지를 확인하고 존재한다면 $v.d$와 $v.\pi$를 update하는 과정이다. 아래 그림의 (a)과 (b)를 보면 무슨 의미인지 알 수 있다.

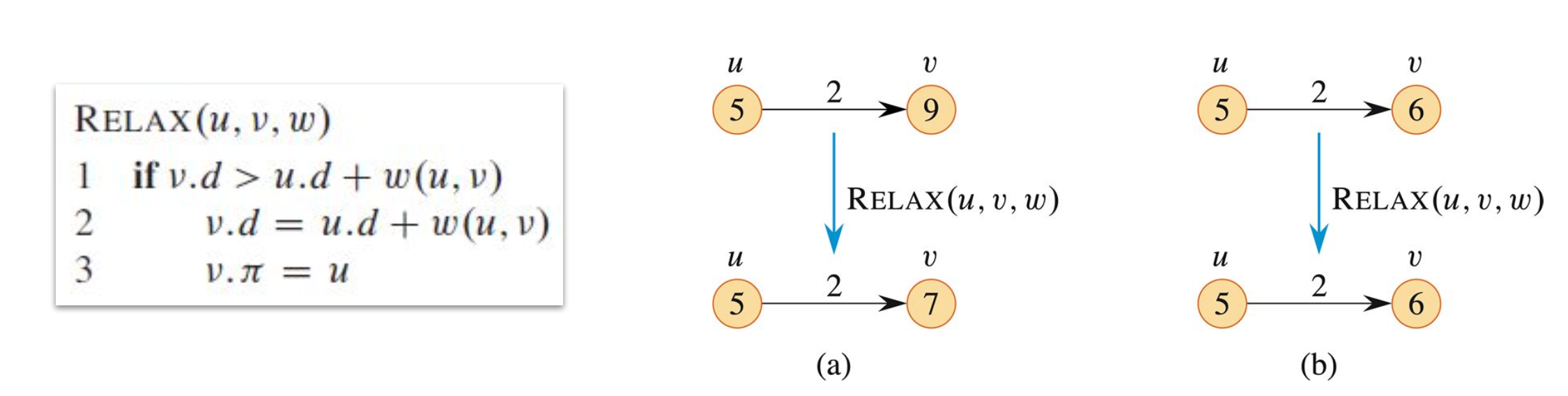
수도 코드로는 기존의 $v.d$ 값보다 $u.d + w(u,v)$의 값이 더 작다면, $v.d, v.\pi$를 update한다. relaxation 단계는 shortest-path estimate를 의미하는 $v.d$의 값을 감소시킨다. 즉, 기존의 경로보다 다른 경로를 거쳤을 때 더 짧은 경로가 있는지 없는지를 확인하는 단계이다.

결론적으로, shortest path를 찾는 알고리즘은 1) initialization 이후 2) relaxation을 반복하는 과정으로 구성된다. 또한 각 edge를 relax하는 횟수와 순서에 따라 shortest path를 찾는 알고리즘이 구분된다.

Properties of Shortest-Path

Triangle Inequality

For all $(u,v) \in E$, we have $\delta(s, v) \le \delta(s,u) + w(u,v)$

shortest path $\delta(s,v)$는 당연히 존재하는 모든 path, $p_{sv}$에 대해 $\delta(s,v) \le w(p_{sv})$를 만족한다. $s$와 $v$ 사이에 $u$라는 vertex가 존재한다고 할 때, $\delta(s,u) + w(u,v)$는 $w(p_{sv})$ 중 하나이므로, 위 property는 성립한다.

Upper-Bound Property

Always have $v.d \ge \delta(s,v)$ for all $v$. Once $v.d = \delta(s,v)$, it never changes.

이에 대한 증명은 앞에서 optimal structure에 대해 이야기하며, 'shortest path의 subpaths는 모두 shortest path가 된다'의 증명과 비슷하다. 귀류법은 사용하자. 만약 $v.d < \delta(s,v)$가 존재한다고 하자. 해당 전제는 $v$가 최초의 vertex이고 $u$ vertex에 의해 $v.d$가 update된다고 할 때, 다음과 같은 식으로 나타낼 수 있다.

$u$에 의해 $v.d < \delta(s,v)$를 만족해야하므로, $u.d = \delta(s,u)$라는 소리가 된다. 그러면 triangle inequality에 의해

이므로 모순이 발생한다.

No-path Property

If $\delta(s,v) = \infin, \text{ then }v.d = \infin$ always

upper-bound property에 의해 항상 $v.d$는 $\delta(s,v)$보다 크거나 같아야한다. 그렇기에 $\delta(s,v)=\infin$이라면 $v.d$도 마찬가지로 무한대가 된다. 또한 이 의미는 $s$와 $v$를 연결하는 path가 존재하지 않는다는 의미이다.

Convergence Property

If $s \rightsquigarrow u \rightarrow v$ is a shortest path, $u.d = \delta(s, i)$, and we call $\text{RELAX}(u,v,w)$, then $v.d = \delta(s,v)$ afterward.

처음의 if절은 'shortest path의 모든 subpaths는 shortest path이다.'에 의해 성립된다. 그리고 $s$에서 $v$로 가는 경로 중에 $u$까지 도달하는 경로가 shortest path이므로, $u$에서 $v$로 가는 경로만 $\text{RELAX}$에 의해 줄어든다면 $s$에서 $v$로 가는 shortest path($=\delta(s,v)$)가 된다. 그렇기에 and절도 성립한다.

Path Relaxation Property

Let $p = \{v_0, v_1, \cdots, v_k \}$ be a shortest path from $s = v_0$ to $v_k$. If we relax, in order, $(v_0, v_1), (v_1, v_2), \cdots, (v_{k-1}, v_k)$, even intermixed with other relaxations, then $v_k.d = \delta(s,v_k).$

upper-bound property에 의하면 모든 vertex에 대해 $v.d=\delta(s,v)$가 되면 이후에 값이 바뀌지 않는다고 하였다. 그럼 경로 $p$에 속하는 vertex를 차례로 잇는 edge 순서대로 $v_{k-1}$까지 relaxation을 해나가면, covergence property에 의해 성립하게 된다.

Predecessor-Subgraph Property

Once $v.d = \delta(s,v)$ for all $v \in V$, the predecessor subgraph is a shortest-paths tree rooted at s.

너무나도 당연하다. 만약 모든 vertex의 $v.d$값, 즉 shortest-path estimate에 해당하는 값이 $\delta(s,v)$, shortest path weight이면, $v$는 $v.\pi$와 연결되는 edge 중에 가중치가 최소값인 edge를 찾은 상태라는 의미이다. 모든 vertex의 $v.d, v.\pi$가 shortest path를 연결하게끔 값이 update된 상태이다.(모든 edge에 대해 relax한 뒤라는 의미) 그렇기에 $v.\pi$로 구성된 predecessor subgraph $G_\pi$는 출발점 $s$를 root로 가지는 shortest-path tree가 된다.