Introduction

한 점에서 다른 점으로 가는 최소 경로를 찾기 위해 방향 그래프로 지도를 모델링할 수 있었다. 방향 그래프로 모델링할 수 있는 것은 이뿐만 아니라 flow network로도 모델링 가능하다. 예를 들면 어떤 물질이 source로부터 흘러들어와서 sink로 빠져나가는 배관을 상상해보자. 이를 방향 그래프로 나타내면 각 edge들은 특정 지점에서 다른 지점을 연결하는 pipe가 된다. 그리고 가중치(weigh)는 edge에 대한 비용이 아닌 물질이 해당 파이프(=edge)를 거쳐 흐를 수 있는 최대 수용량, 용량(capacity)을 의미한다. 물론 위 가정에서 유량(flow)이 유체가 아니여도 된다. 예를 들면 택배를 트럭으로 옮기는 상황을 가정해도 된다. 출발지에서 택배를 담아 도착지 터미널로 이동할 때, 중간에 허브 터미널을 거치게 된다. 이때 트럭에 최대로 담을 수 있는 택배의 양을 용량(capacity)로 줄 수도 있을 것이다. 또한 이런 상황을 가정했을 때 maximum flow problem은 출발지에서 도착지로 얼마나 많은 택배를 보낼 수 있는가? 가 될 것이다.

더 일반화하면, soruce에서 sink로 흐를 수 있는 최대 유량이 얼마인지를 계산하는 문제가 maximum flow rate라고 볼 수 있다.

Flow Network

flow network는 방향 그래프 $G = (V, E)$로 표현한다. 이때 각 edge$(u, v)$는 capacity $c(u,v) \ge 0$를 만족해야한다. 만약 $(u,v) \notin E$이면, $c(u,v) = 0$이다. 그리고 $(u,v) \in E$이면, reverse edge인 $(v,u) \notin E$가 됨에 주의하자. 그리고 구분되는 두 vertex인 source $s$와 sink $t$에 대해 $s\rightsquigarrow v \rightsquigarrow t$의 관계를 모든 vertex, $v \in V$에 대해 만족한다고 가정하자.

Flow

Maximum flow problem에서 구해야 하는 것은 결국 각 edge마다 흐를 수 있는 'flow(유량)'이다. 유량을 다음과 같은 함수로 정의한다고 하자.

그리고 $f$는 1) capacity constraint와 2) flow conservation 을 만족해야한다.

• 1) For all $u, v \in V$, $0 \le f(u,v) \le c(u,v)$
• 2) For all $u \in V - \{s,t\}$,
  $\sum_{v \in V} f(v, u) = \sum_{v \in V} f(u, v)$

정리하면, 유량은(flow) 최대 유량인 용량(capacity)를 넘지 않아야 하고 해당 vertex로 들어오는 양과 나가는 양은 같게끔 정해져야 한다. 그리고 $f$의 값은 $|f|$로 표기하며, 이는 다음과 같이 구할 수 있다.

Maximum Flow Problem

최대 유량 문제는 방향 그래프 $G$와 source $s$, sink $t$, capacity $c$가 주어졌을 때, 그래프 $G$의 최대 값을 갖는 flow를 찾는 문제이다. 그런데 우리는 주어지는 방향 그래프 $G$에 대해 어떠한 제약 조건도 달지 않았다. 예를 들면 'cycle을 가져서는 안된다'가 있을 것이다. 이렇게 제약 조건을 달지 않는 이유는 최대 유량 문제를 풀 때 방향 그래프는 일반화가 가능하기 때문이다. 우선 방금 든 예시와 같이 'cycle'에 대해 생각해보자.

Cycle

방향 그래프에서 cycle은 결국 루프(loop)이다. 자기자신으로 다시 돌아오는 edge를 의미하는데, flow network에서 루프는 아무 의미가 없다. flow는 flow conservation을 만족해야하기 때문이다. 그렇기에 flow network에는 cycle, 즉 루프가 존재하지 않는다고 할 수 있다.

Parallel Edges

머리(head)와 꼬리(tail)가 동일한 edge를 평행 간선(parallel edge)이라고 한다. 하지만 다음과 같은 과정을 통해 flow network에는 이러한 평행 간선이 존재하지 않는다고 말할 수 있다.

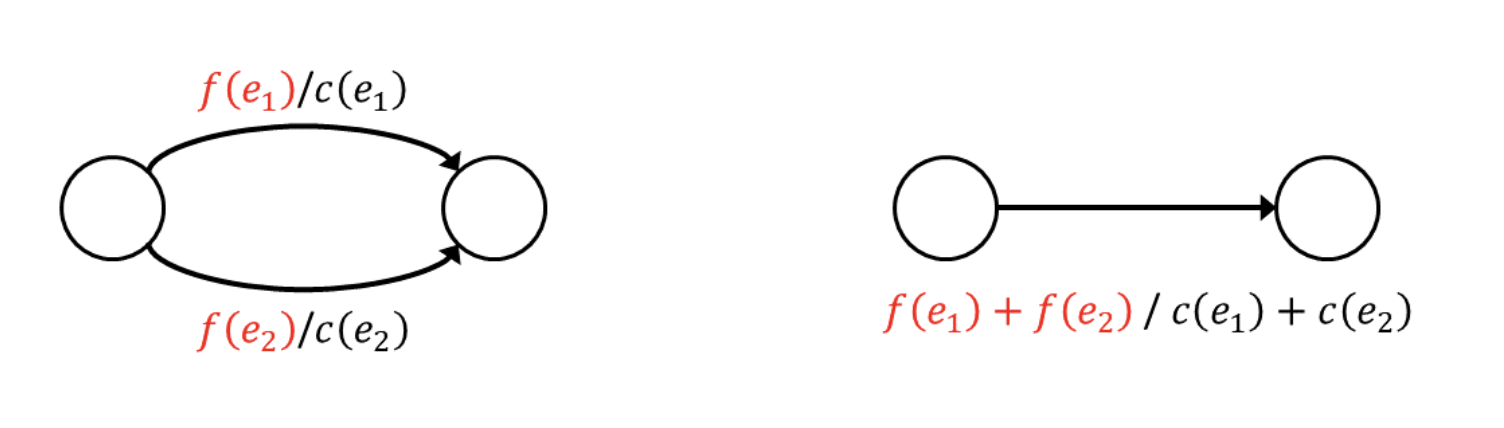
"출처 https://gazelle-and-cs.tistory.com/60"

위와 같이 동일한 방향을 갖는 edge가 2개 존재하여도 하나로 합칠 수 있다. 이 과정을 parallel edges에 대해 적용하면 결국 parallel edge가 없는 그래프와 동일하다.

AntiParallel Edges

사실 앞에서 edge에 대한 제약 조건을 하나 달았었다. 해당 조건은 $(u,v) \in E$이면 $(v,u) \notin E$였다. 즉 특정 방향을 갖는 두 vertex를 연결하는 edge가 존재하면, 해당 edge의 역방향 edge는 존재하지 않는다는 것이다. 그런데 사실 이 조건이 없어도 큰 문제는 없다. 그 이유는 다음 그림을 보면 알 수 있다.

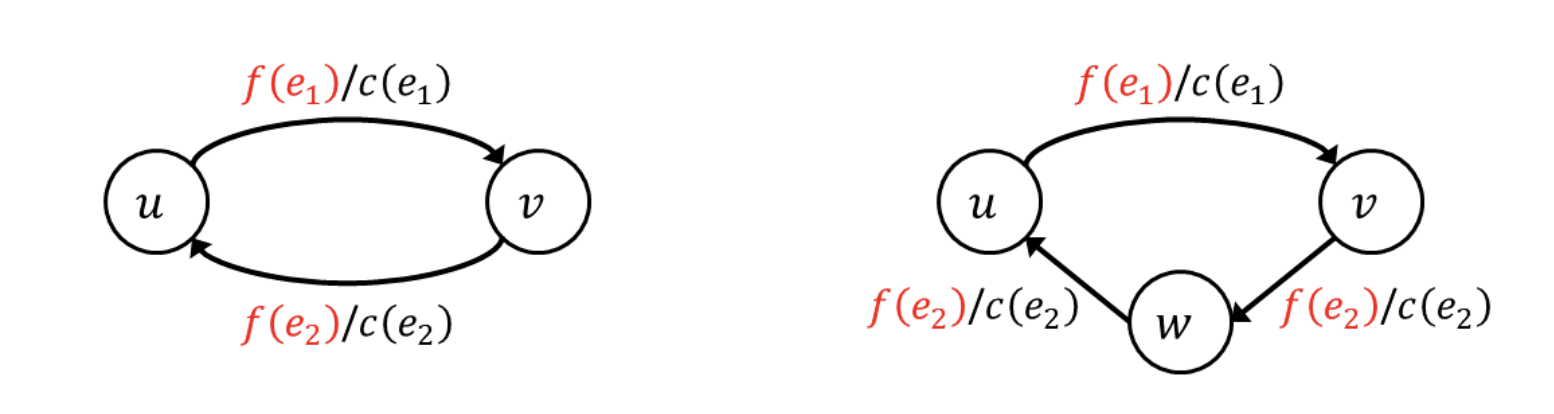
"출처 https://gazelle-and-cs.tistory.com/60"

즉, 역평행 간선(antiparallel edge)가 존재한다면, 새로운 node(=vertex)를 만들고 해당 node와 기존 node를 연결하는 edge를 추가하여 antiparallel edges가 존재하지 않는 그래프로 만들 수 있다.

결론적으로 flow network는 루프 / 평행 간선 / 역평행 간선이 존재하지 않는 방향 그래프이다. 라고 말할 수 있다.

Multiple Sources and Sinks

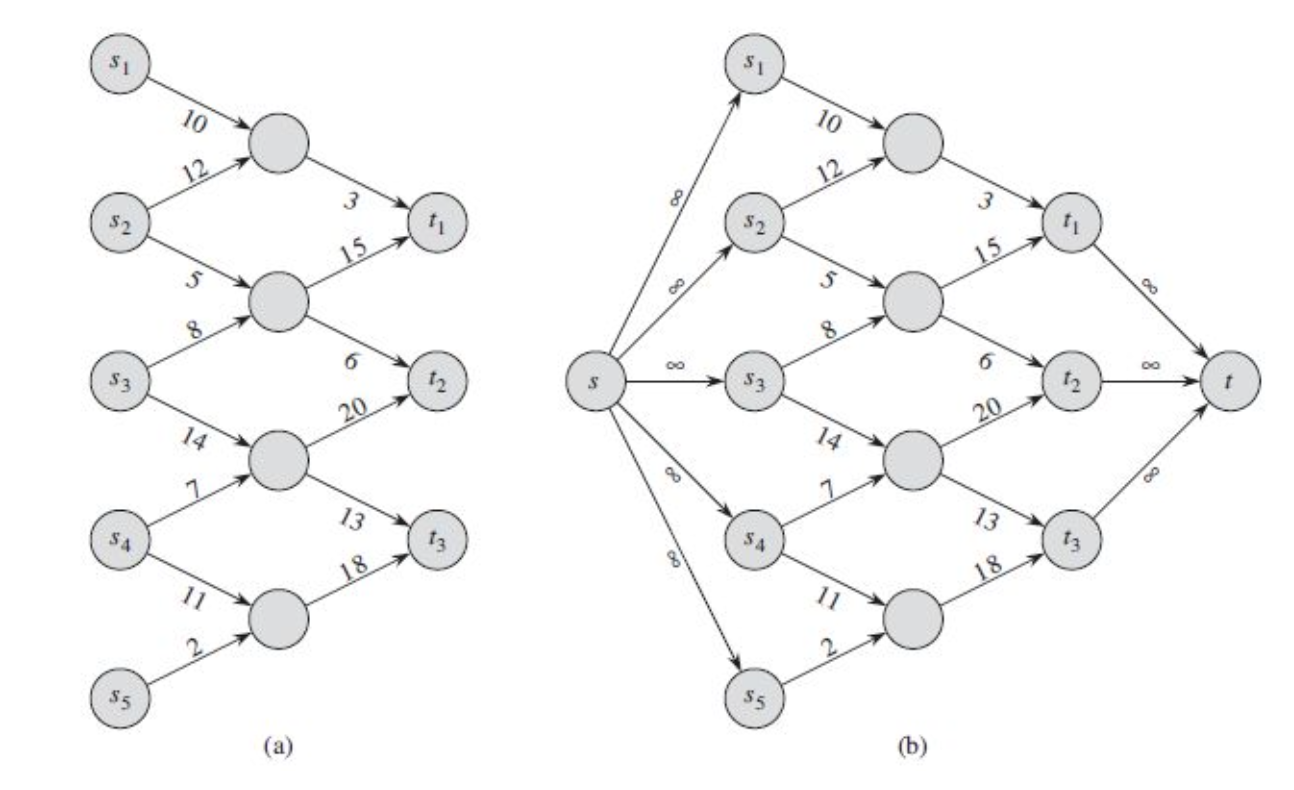
여러개의 source와 sink가 존재하는 flow network에 대해 최대 유량을 구하고자 한다면 어떻게 해야할까? 이는 supersource와 supersink라는 개념을 통해 간단히 일반적인 flow network로 만들 수 있다. 위 그림 (a)를 (b)로 만드는 것이다. supersource를 $s$라고 하고, edge$(s, s_i)$를 추가해주면 된다.

sinks에 대해서도 마찬가지이다. supersink를 $t$라 정의하고, edge$(t_i, t)$를 추가해주면 된다.

Residual Network

앞에서 flow network를 표현하는 방법과 여러 정의에 대해 다루었다. 이제 어떻게 주어진 flow network에서 maximum flow를 구할 수 있는지 알아보자. maximum flow를 구하기 위해 사용되는 것이 바로 잔여 네트워크(Residual Network)이다. 다음과 같은 간단한 예시를 살펴보자.

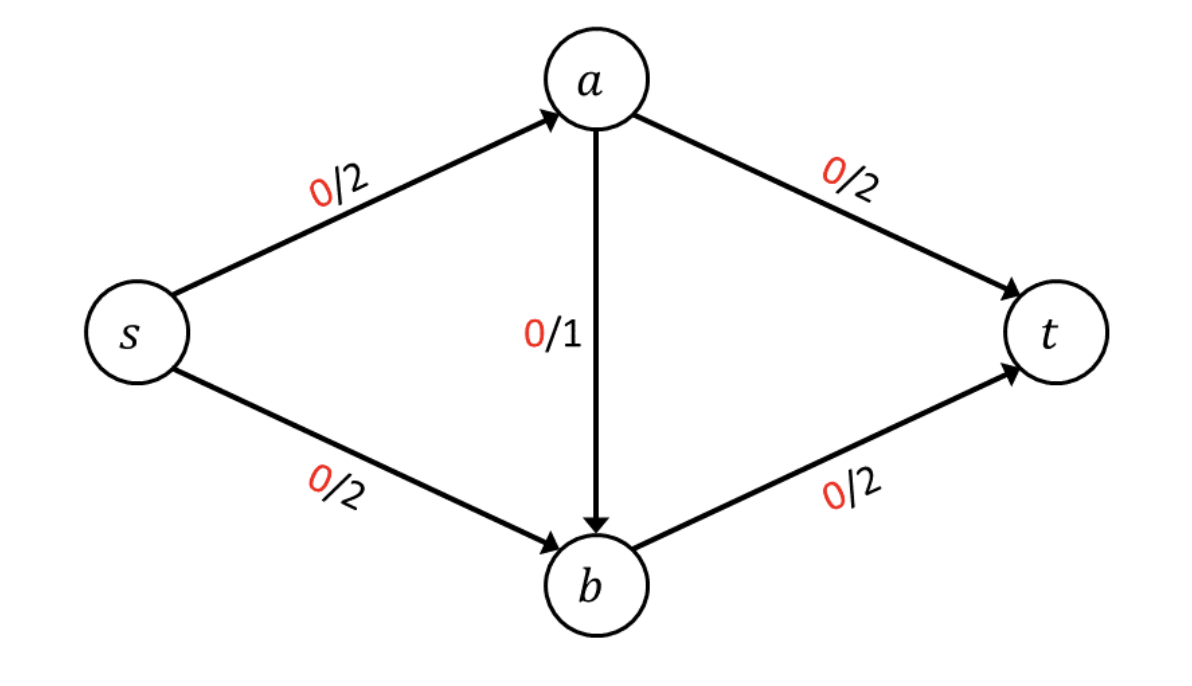
위와 같은 flow network가 주어졌다고 하자. 각 edge마다 얼마의 flow를 흘려보내야 maximum flow가 될까? 우선 $(s, a), (a,b), (b,t)$의 edge를 지나는 경로로 1만큼의 유량(flow)를 흘려보냈다고 가정하자. 1보다 큰 유량은 $c(a,b)$에 의해 흘려보낼 수 없다. 그리고 $(s,a), (a,t)$와 $(s,b), (b,t)$로 1씩 더 흘려보낸다고 가정하자. 더 이상 추가할 수 있는 flow가 존재하지 않게된다. 이때의 flow는 3이되는데($s$에서 출발한 양이 3이므로 flow conservation에 의해 flow network를 흐르는 유량은 3이다.), 이것이 maximum flow일까? 그렇지 않다. 중간에 $(s, a), (a,b), (b,t)$의 edge를 지나는 경로로 1만큼의 유량(flow)을 보내지 않고, 바로 $(s, a), (a,t)$로 2씩 흘려보낸다면 최대 유량은 4가 된다. 즉, $(a,b)$를 지나갈 이유가 없다. 우리는 사람이기에 잘못된 경로를 찾아내어 수정할 수 있다. 하지만 컴퓨터가 이를 어떻게 연산할까? 잘못된 경로로 flow를 주었을 때 다시 처음으로 돌아가 계산을 해야할까?

$(a,b)$를 지나가는 경로를 취소하는 것이 아니라, $(s,b)$로 1의 흐름을 더 준다고 가정해보자. 그럼 flow conservation에 의해 $b$에는 1의 초과 유량이 존재한다. 이를 상쇄하기 위해 $(b,a)$로 1을 흘려보낸다고 하자. 그럼 다시 $a$에도 1의 초과 유량이 발생하고 이를 상쇄하기 위해 $(a, t)$로 1을 흘려보내면, capacity constraint와 flow conservation을 만족하는 flow가 형성되고, 최대 유량은 4가 된다. 이 과정을 개념화한 것이 바로 Residual Network이다.

Residual Capacity

residual network를 구하기 위해서는 residual capacity를 구해야 한다. 이는 다음과 같이 정의된다.

residual capacity를 활용해 residual network의 간선 $E_f$를 다음과 같이 정의한다.

그러면 residual network는 $G_f=(V, E_f)$이다. residual capacity를 구하여 residual network를 구해보면 다음과 같다.

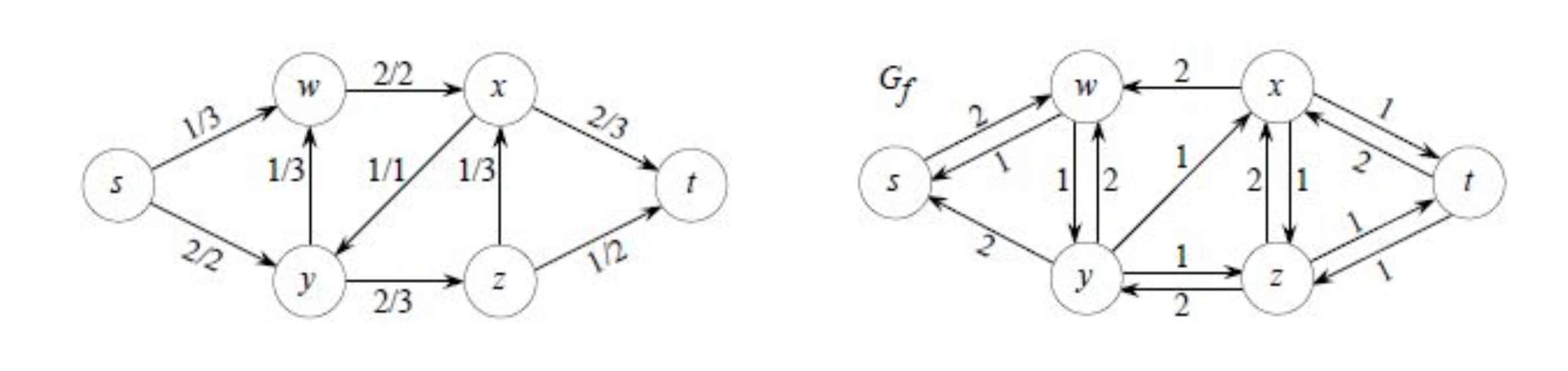
$c_f(s,w)$는 $(s,w) \in E$이므로 첫번째 case로 $3-1=2$가 된다. $c_f(w,s)$는 $(u,s) \in E$이므로 두번째 case라 $1$이 된다. 해당 과정을 모든 edge $(u,v) \in V \times V$에 대해 적용하여, $c_f$를 구하고 이를 통해 $G_f$를 그리면 위 그림의 우측 그래프와 같다. residual network로 알 수 있는 점은 기존 그래프의 방향과 동일한 edge에 residual capacity가 존재하면, 해당 양만큼 더 flow를 가할 수 있다는 의미이고, 역방향 edge에 residual capacity가 존재하면, 해당 양만큼 flow를 취소할 수 있다는 의미이다. 아주 중요하다!

Augmenting Path

residual network를 통해 어떻게 maximum flow를 구할 수 있을까? residual network를 구한 이유는 어떤 flow가 그래프 상에 존재할 때, 이를 기반으로 현재 최대 유량보다 더 많은 flow를 가하는 방법을 찾기 위함이다. 우선, 임의의 흐름 $f$에 대한 residual capacity $c_f$를 구하고, residual network $G_f$를 구했다고 하자. 여기서 $s$와 $t$를 잇는 아무 경로 $p \subseteq E_f$를 가정하자. 해당 경로 $p$를 augmenting path라 한다.

$c_f(p)$

경로 $p$에 대한 residual capacity, $c_f(p)$를 다음과 같이 정의하자. edge에 대한 residual capacity가 아닌 경로(path) $p$에 대한 residual capacity임에 주의하자!

그리고 이 경로에 존재하는 edge에 대한 흐름(flow), $f^{\prime}(u,v)$을 다음과 같이 정의하자.

Augmentation

그리고 augmentation 연산을 적용한다. augmentation은 다음과 같다.

이제 위에서 예시로 든 $G, G_f$에 augmenting path를 다음과 같이 정의하자.

그럼 $c_f(p) = c(w,y) = c(y,z) = c(x,t) = 1$이 된다. 그러므로 $f^{\prime}(e) = 1\text{, where }e \in p$. 이를 바탕으로 augmentation $f \uparrow f^{p}(e)$를 수행하면, 그 결과는 아래 그림의 오른쪽 그래프와 같다.

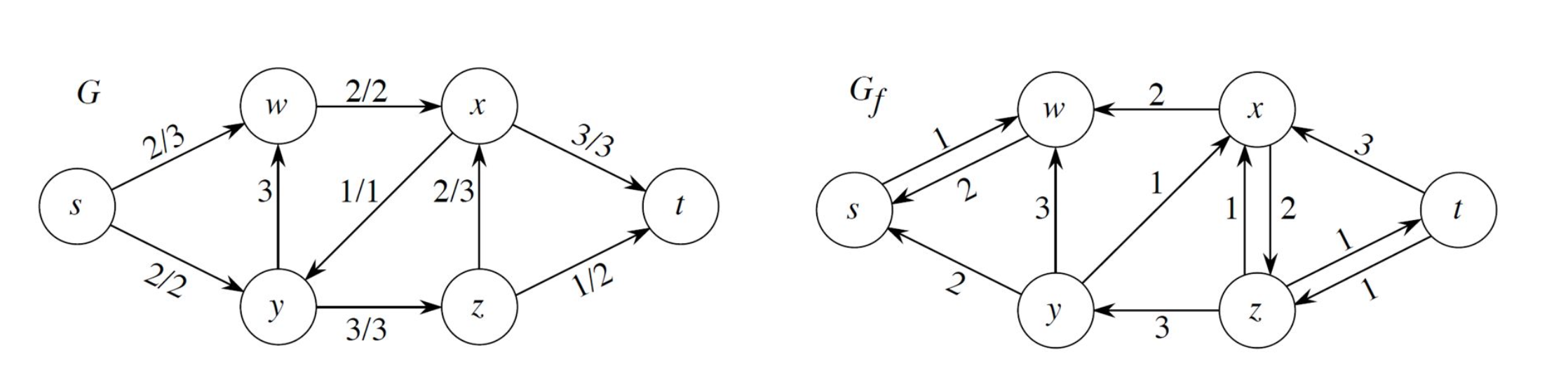
residual network를 구하고 augmentation 연산을 수행한 결과로 얻어진 $G$의 flow는 이제 4가 되었다. 기존의 flow network의 flow는 3이였다. 그렇다면 4가 주어진 flow network의 최대 유량일까? 이를 확인하기 위해 새로운 residual network $G_f$를 구해본다. 이는 위 그림의 오른쪽 그래프에 해당한다. $G_f$에서 $s$와 $v$를 잇는 어떠한 augmenting path, $p$를 찾을 수 없다. 그렇기에 현재 그래프 $G$의 flow가 주어진 flow network의 최대 유량이 된다.