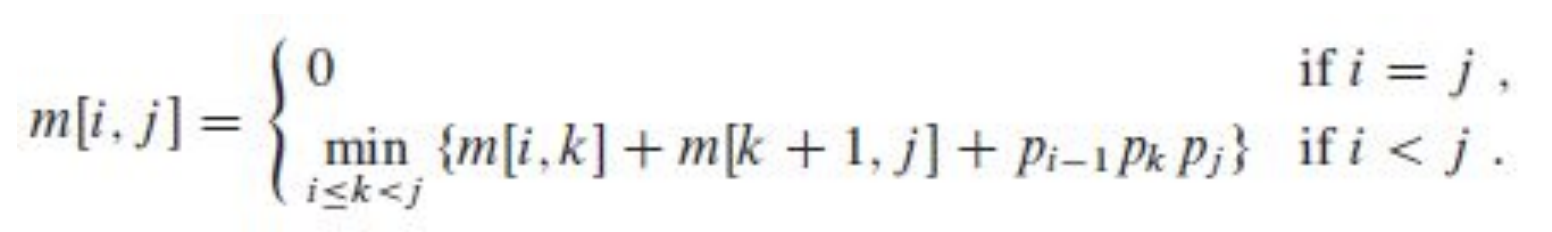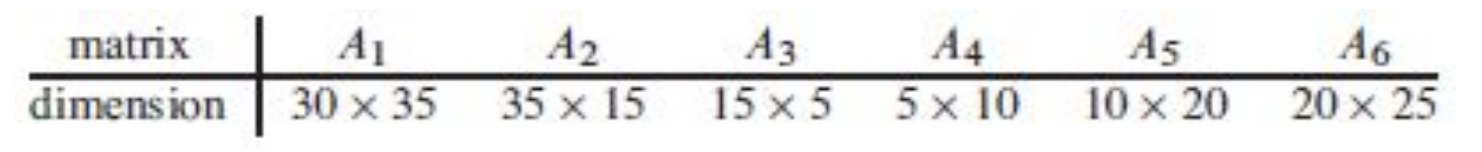Matrix-Chain Multiplication

두 행렬의 곱은 다음과 같은 수도 코드로 계산된다는 것은 당연한 사실이다.

그런데 만약 행렬이 여러 개인 경우, 최적의 연산 횟수는 어떻게 될까? 두 행렬을 곱하는 연산 횟수를 단순히 곱한 것으로 동일할까? 만약 행렬의 크기가 제각각이라면 그렇지 않다.

만약 $n$개의 행렬이 담겨 있는 sequence를 가정해보자. 곱하는 순서를 괄호로 묶어 표시한다면, 연산 순서를 나타내는 방법은 총 몇가지가 있을까? 예를 들어 $n=4$라면, sequence에는 $\langle A_1, A_2, A_3, A_4\rangle$가 있게 된다. 이 때 괄호로 묶어 연산 순서를 지정하는 방법은 총 5가지이다.

이렇게 연산 순서를 구분하는 방법에 따라 실제로 연산 횟수가 달라질까? 아래의 예시를 살펴보자.

연산 횟수가 달라지는 이유

sequence는 $\langle A_1, A_2, A_3\rangle$이 존재한다고 가정하자. 각 행렬의 크기는 $10\times100, 100\times5, 5\times50$이다. 이 때, 연산 순서를 구분하는 방법은 2가지이다.

1. $((A_1, A_2), A_3)$
2. $(A_1, (A_2, A_3))$

1번 경우일 때, $A_1, A_2$의 행렬 곱을 먼저하기 때문에, 연산 횟수는 $10\times100\times5=5000$이고, 그 다음 $A_3$과 곱하게 되면, $10\times 5 \times 50=2500$번 연산하게 되어 총 $7500$의 연산 횟수가 필요하다.

2번 경우일 때는 $A_2, A_3$의 행렬 곱을 먼저 계산하면, $25000$번 + 그 후 $A_1$ 행렬과 곱하면 $50000$번의 연산이 수행되어 총 $75000$의 연산 횟수가 필요하다.

즉, 1번 경우가 2번 경우보다 무려 10배나 더 빠르다. 이처럼 연속된 행렬의 곱셈을 수행할 때 연산 횟수가 가장 적게 만드는 방법을 찾는 문제를 Matrix-Chain Multiplication Problem이라고 한다.

Brute-Force Algorithm

완전 탐색하는 경우를 가정하면, $P(n)$을 $n$개의 길이를 갖는 연속된 행렬의 곱을 계산 순서를 정하기 위해 괄호로 묶는 서로 다른 방법의 수라고 정의하자. 그럼 brute-force의 $P(n)$은 다음과 같다.

시간복잡도는 어떻게 될까? 우선 $n$을 5까지 대입해보며 차례차례 구해보자. 그럼 $P(2)=1, P(3)=2, P(4)=5, P(5)=14$로 나오게 되는데, substitution method로 구해보자. $n$을 대입해보며 구한 값으로 우리는 다음과 같이 유추할 수 있다.

n=1일 때, 가정한 식에 그대로 대입하면 $P(1)=1$이므로 참이다. 그 후 $k>5$에 대해 $P(k) \ge 2^{k-2}$가 참인지 확인하면 옯은 가정이라 할 수 있다.

그 후, $P(n) \ge 2^{n-2}$인지 확인해보면,

따라서 $P(n) \in \Omega(2^n)$임이 증명되었다. 어찌됐든 완전 탐색으로 문제를 풀면, 시간 복잡도는 polynomial expression이 아니라 exponential한 bound를 가지게 되기 때문에 비효율적이라는 것은 알 수 있다.

Applying Dynamic Programming

이번에는 DP 기법을 적용해보고, 시간 복잡도가 얼마나 차이나는지 알아보자. 우선 4개의 단계로 DP 기법을 문제에 적용할 수 있다고 하였다.

1. 최적해의 구조 특징 파악 = optimal substructure가 있는 지 확인!
2. 최적해의 값을 구하기 위해 재귀적으로 호출. = 어떻게 호출할 것인지 정의
3. 각 재귀 호출마다 값을 계산
4. 계산된 값들로 최적해를 형성

Step 1 :

우선 DP 기법으로 문제를 풀기 위해서는 optimal substructure가 있어야 한다. 문제 구조에 최적 부분구조가 존재하는지 어떻게 확인할 수 있을까? 그 증명은 다음과 같다.

Proof by Contradiction

만약, 다음과 같이 묶는 경우가 최적의 경우라고 가정하자.

간단히 표기하기 위해 괄호로 묶은 항 중에 첫번째 항을 $A_{1...i}$라 하고, 두번째 항을 $A_{i+1...n}$이라고 하자. 이 때가 최적의 해라고 가정했기 때문에, 연산 횟수의 총 합은 무조건 최소값이 된다. 각 연산 횟수를 다음과 같이 정의하자.

1. $A_{1...i}$의 행렬 곱을 계산하는 연산 횟수를 $X$라 하고,
2. $A_{i+1...n}$의 행렬 곱을 계산하는 연산 횟수를 $Y$,
3. 마지막 두 행렬의 연산 횟수를 $Z$라 정의하자.

그럼 $X+Y+Z$가 최소값인데, 만약 $A_{1...i}$의 경우가 최적의 경우가 아니라면, $X^{\prime} < X$인 $X^{\prime}$이 존재하게 된다. 이 말은 곧, $X^{\prime}+Y+Z$가 최소값이기 때문에 모순이 발생한다. 결론적으로 $i$를 기준으로 나눈 것이 최적의 구조라면, 총 연산 횟수도 자동적으로 최적의 해가 된다.

즉, subproblem의 optimal solutions로 부터 원래 문제의 optimal solution을 도출할 수 있다는 뜻이고, 이는 문제가 optiaml substructure를 가진다는 의미이기에 DP 기법을 적용할 수 있다.

Step 2

이제 재귀적으로 어떻게 호출할 것인지 결정하자. 어떤 행렬 $A_i$의 크기를 $p_{i-1} \times p_i$라 정의하자. 그리고 DP 기법을 적용하기 위해 이전 연산 결과를 저장하는 배열 $m$을 정의하고, $m[i, j]$에는 $A_{i...j}$의 최적 연산 횟수(최소 연산 횟수)를 저장한다고 하자. 만약 $k, (i\le k\le j)$로 나눌 때가 최적이라면, $A_{i...j}$의 최소 연산 횟수($m[i, j]$에 저장되는 값)는 다음과 같이 정의된다.

만약, $i=j$의 경우에는 배열 $m$에 0이 저장된다.

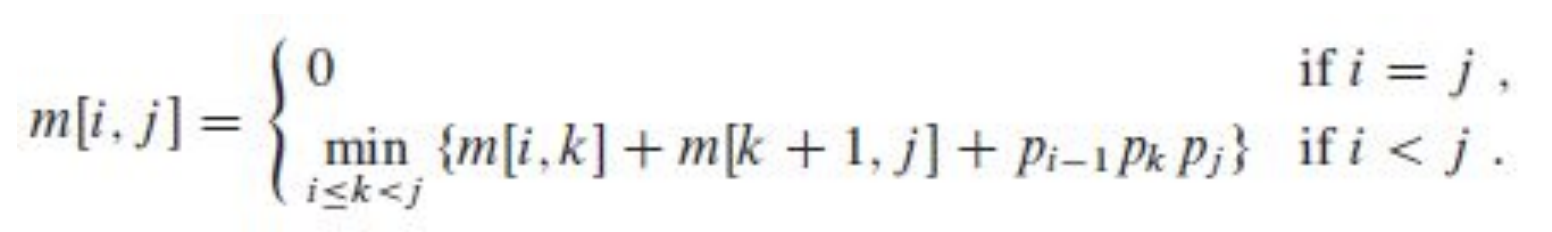
그리고 추가적으로 배열 $s$를 정의하여, $s[i, j]$에는 최적으로 나눈 $k$값을 저장한다고 하자.

Step 3

Step 2에서 정의한 재귀적인 호출 방법에 의해 계산하는 수도 코드와 배열 $m$의 값은 다음과 같다.

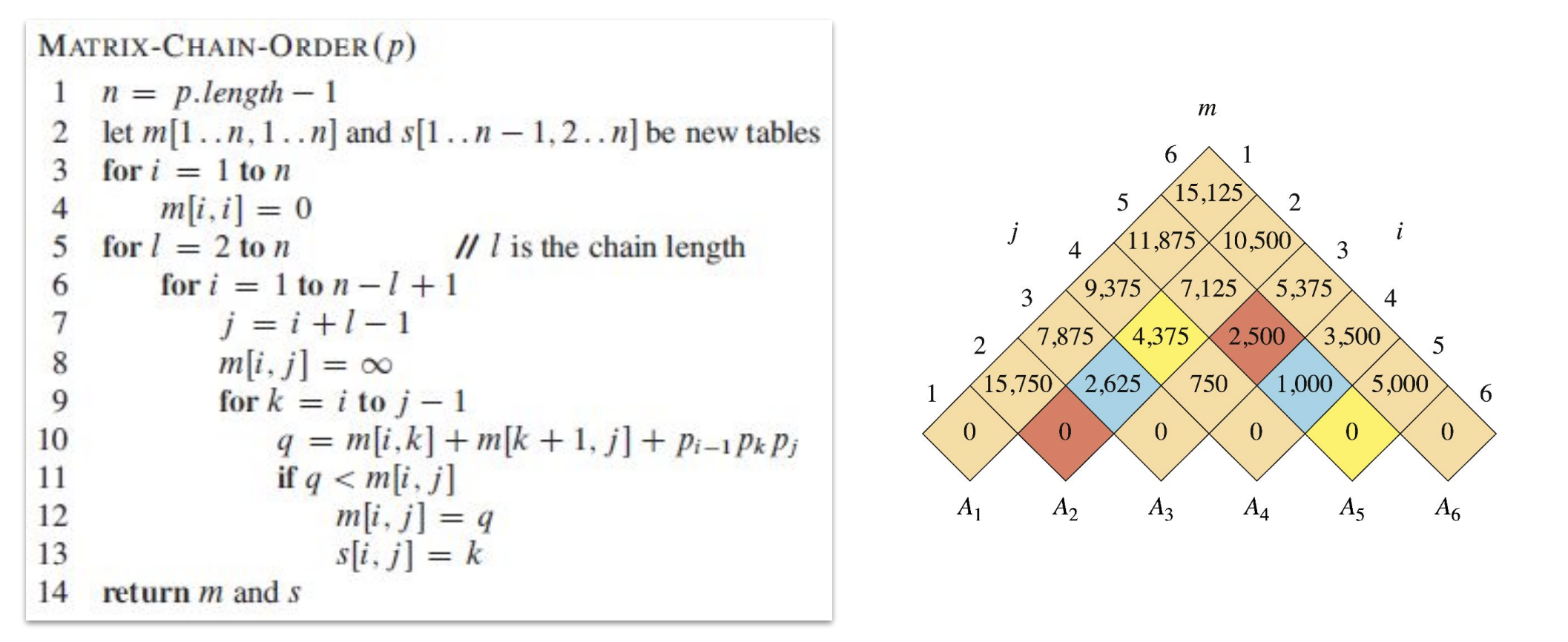
위의 예시는 $n=6$인 경우이다. 각 행렬의 크기는 다음과 같다.

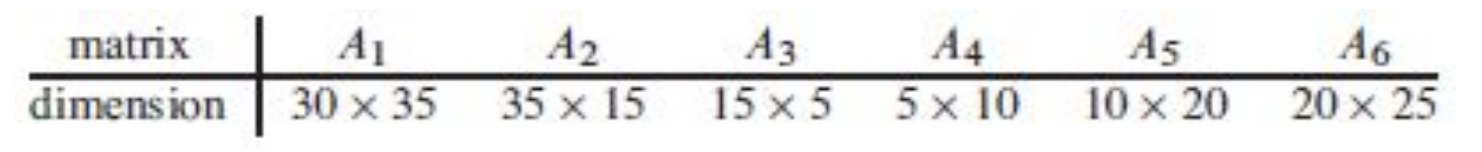
Step 4

$n=6$일 때, input에 대하여 계산된 결과는 다음과 같다.

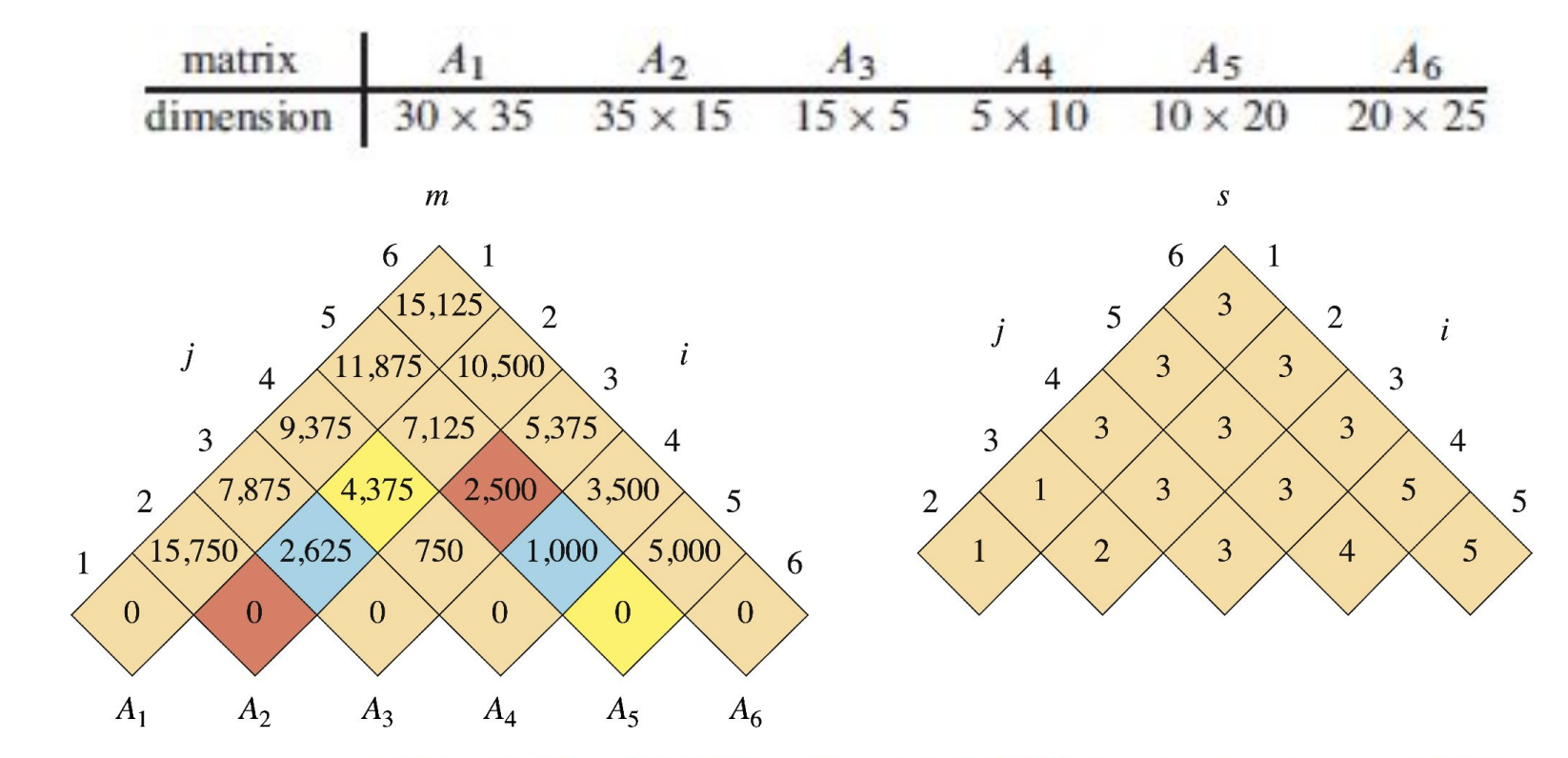
이를 활용해 최적의 해를 구하는 수도 코드는 다음과 같다.

그럼 답은

PRINT-OPTIMAL-PARENS(s, 1, 6)

을 실행한 결과로,

이 출력될 것이다. 시간 복잡도는 Step 3의 수도 코드를 보면 알 수 있듯이 반복문을 3번 돌기 때문에 $O(n^3)$이라 예상할 수 있다.

Prove of $O(n^3)$

직관적으로 3중 반복문을 보는 순간, 우리는 $O(n^3)$이라 예상할 수 있지만 실제로 그런지 증명해보자. 배열 $m$에 접근하는 횟수를 연산 횟수라고 가정하자. DP 기법으로 Matrix chain multiplication problem을 푸는 수도 코드는 위에서 정의했었고, 그럼 총 연산 횟수는 $R(i, j)$이다.

우선 첫번째 반복문에서 변수 $l$이 2에서 $n$까지 돌게 되면서 $n-1$번 반복한다는 사실을 알 수 있다.
두번째 변수 $i$에 대한 for문은 $n-l+1$번 반복한다. 세번째 변수 $k$는 $j-i$번 반복하는데, 여기서 $j=i+l-1$이므로 반복 횟수는 $l-1$번이다. 다만, 이 때 두 번 배열 $m$에 접근하기 때문에 2를 곱해준다. 그럼 최종 연산 횟수는

그러므로 $T(n)=\frac{n^3 - n}{3} \in O(n^3)$임이 증명되었다.