Longest Common Subsequence Problem
두 개의 수열 가 주어진다. 수열 로 정의되고, 로 정의하자. 우리가 구해야하는 것은 "subsequence common to both whose length is longest"이다. 즉, 두 수열의 공통된 요소를 포함하는 subsequence 중에 가장 긴 것을 찾는 문제이다. 여기서 주의할 점은 하위수열(subsequence)는 연속적이지 않아도 되지만 순서는 따라야한다는 것이다. 예를 들어, , 이 주어지면 LCS는 또는 가 된다.
Brute-Force
완전 탐색으로 문제를 해결하면 의 모든 subsequence가 의 subsequence가 되는지를 하나하나 확인해야한다. 의 subsequence는 개이고, 수열 에는 개의 요소가 있기 때문에 총 번 확인해야 한다. 즉, 시간 복잡도가 , exponential time을 갖게 된다.
DP
Step 1
두 개의 수열 를 끝에서 부터 비교해나가며 같은 부분을 수열 에 저장해나간다면, 는 LCS가 될 수 있다. 같지 않은 경우에는 두 가지 경우로 나눌 수 있다. 첫번째로, 인 경우는 가 와 의 LCS가 될 것이다. 두번째로 인 경우는 가 과 의 LCS가 될 것이다. 즉, 뒤에서부터 재귀적으로 호출해나가며 끝 부분을 비교해나가며 구한 optimal solution인 를 통해 구하는 수열 가 결국 LCS가 되기 때문에 optimal substructure를 가진다고 볼 수 있고, DP를 통해 문제를 해결할 수 있다.
Step 2
Step 1에서 이야기한 LCS 문제의 optimal substructure를 정리하면 다음과 같다.

배열 를 새로 정의하여 와 의 LCS 길이를 에 저장한다고 하자. 그럼 그 값은 위 정의에 의해 다음과 같다.
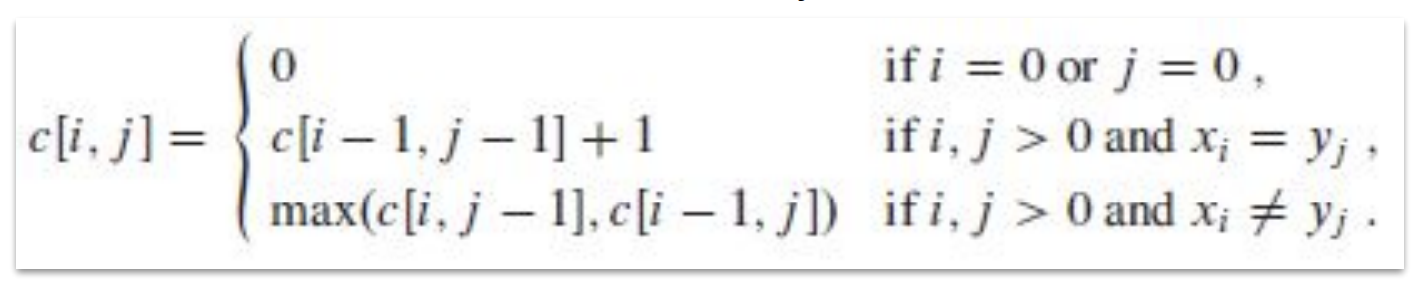
Step 3
값들을 계산하기 위해 수도 코드로 작성하면 다음과 같다.

이 때, 배열들을 채워나가며, 의 값을 구할 때 값에 해당하는 값이 2차원 배열 의 어디에서(대각 or 옆 or 위) 참조했는 지를 기록하기 위해 배열 를 새로 정의하여 기록한다.
Step 4
계산 결과를 이용해 LCS를 구한다. 우선 계산 결과는 아래 표와 같다. 배열 와 에 저장되는 값을 편의상 한 표에 같이 나타내었다.
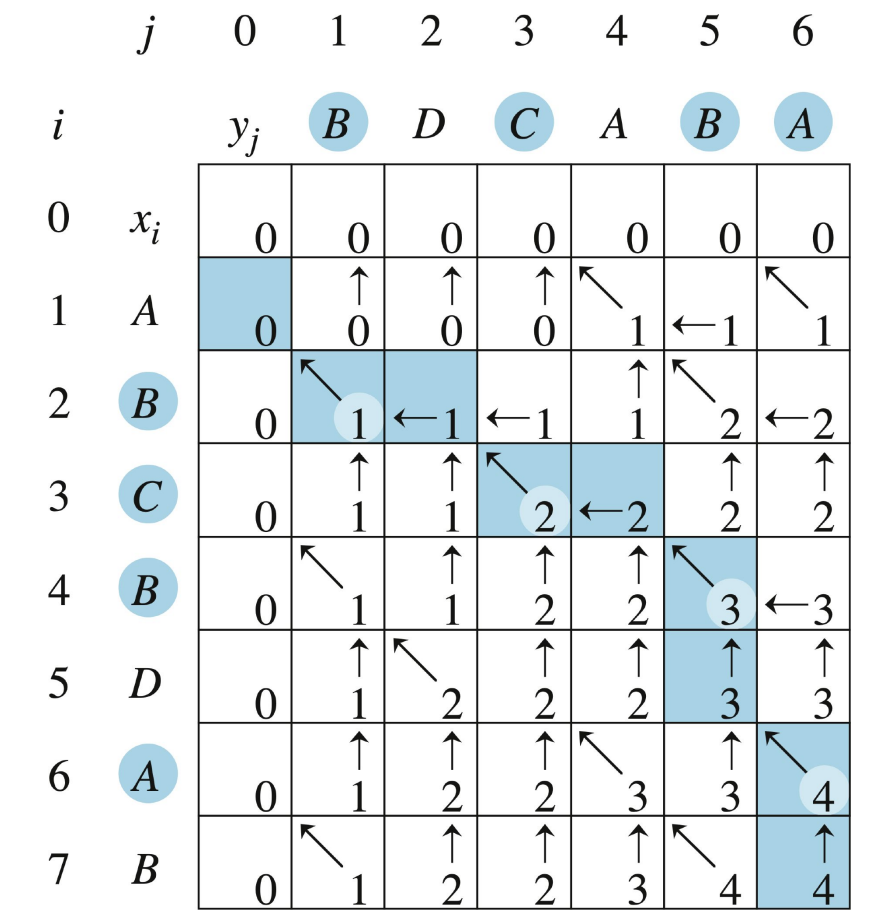
LCS를 구하는 수도 코드는 다음과 같다.

우리가 예시로 든 와 를 input으로 배열 를 계산하였고, 위 수도 코드에 따라 LCS를 출력하면 된다. 그런데 여기서 어떤 값을 PRINT-LCS 함수에 넣어야할까? 간단하다. LCS는 두 수열의 중복된 요소를 포함하는 subsequence 중에 가장 긴 subsequence이므로, 배열 의 값 중 최대인 를 함수의 parameter로 넣으면 된다. 그럼 위의 표의 경우에는
가 될 것이다. 물론 역순으로 출력한 것이기 때문에(뒤에서 부터 탐색해 나가니까), 가 답이 된다.
Optimal Binary Search Trees
이진 탐색 트리는 rooted binary tree의 자료구조를 따른다. 각각의 node는 key값을 저장하게 되고, root부터 내려오면서 node의 key값보다 큰 경우 오른쪽으로, 작은 경우 왼쪽으로 이동해나가며 rooted binary tree를 완성해나간다. 여기서 최적 이진 탐색 트리(Optimal binary search tree)는 가장 작은 가능한 search time을 제공하는 binary search tree이다. 즉, root node에 어떤 key값을 저장하냐에 따라, 다른 구조의 이진 탐색 트리가 만들어지게 되고, 그 때 cost 기대값이 달라지게 된다. 그렇기에 최적 이진 탐색 트리는 기대값이 가장 작은 이진 탐색 트리를 의미한다.
기대값(Expectation)
기대값은 어떻게 계산할까? 각 변수 에 대한 기대값 는 각 변수 의 확률 를 서로 곱한 것의 합, 즉 로 나타낼 수 있다. 이진 탐색 트리의 기대값은 다음과 같이 구할 수 있다.
우선, 주어진 수열 이 개의 구별되는 key라고 하자. 순서는 사전에 정렬되어 있는 상태이다. 이 때 에 포함되지 않는 "dummy keys"가 개 있게 된다. 각 dummy key들은 로 정의 된다. 이 때, 를 탐색하게 되는(찾는) 확률을 , 를 찾는 확률을 라고 각각 정의하자. 확률의 합은 모든 경우를 합한 경우에 1이 되기 때문에 다음은 자명한 사실이다.
왜 key와 dummy key들을 이진 탐색 트리의 기대값을 구하는데 이야기했을까? 다음 예시를 보면 이해가 될 것이다. 만약 에 5개의 key들이 존재하면, 이 key들로 이진 탐색 트리를 완성한 뒤, leaf node들이 dummy key들이 될 것이다. 그럼 dummy keys는 총 6개가 된다.
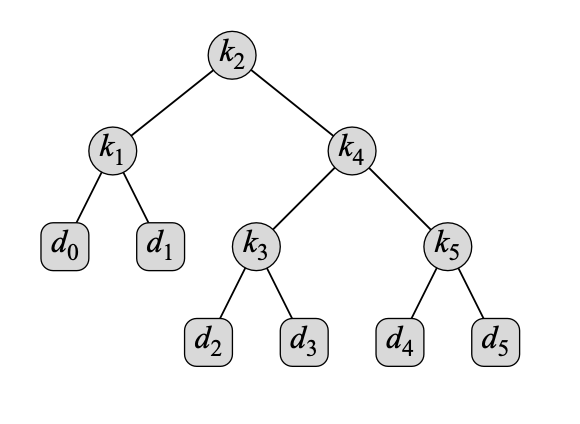
위 그림은 를 root node의 값으로 설정한 뒤 이진 탐색 트리를 완성한 결과이다. 이 이진 탐색 트리의 기대값은 어떻게 계산할까? root부터 차례로 depth를 내려가게 되며 모든 node들을 순회하며 어떤 값을 찾게 될 것이라 예상할 수 있다. 그럼 특정 depth에 우리가 원하는 값을 가지는 node를 찾지 못하는 경우에 depth를 한 칸 더 내리게 된다. 이는 곧 기대값에서 연산을 해준다는 의미로 가정하자. 그럼 다음과 같이 어떠한 이진 탐색 트리 의 cost 기대값을 식으로 나타낼 수 있다. 그리고 root node의 depth는 0이므로 0에 어떠한 값을 곱해도 0이 되는 것을 방지하기 위해 에 확률을 곱하며 기대값을 구한다.
분배법칙을 적용하고, 시그마의 연산 규칙을 적용하면 임을 이용하여 간단히 구할 수 있다.
Step 1
이제 DP 기법을 적용하여 문제를 풀기 위해 optimal substructure가 있는지 고려해보자. 결국 주어진 key와 dummy key들로 만들 수 있는 이진 탐색 트리는 root node에 어떤 값이 오냐에 따라 결정된다. 즉, 다음과 같은 형태를 가진다.
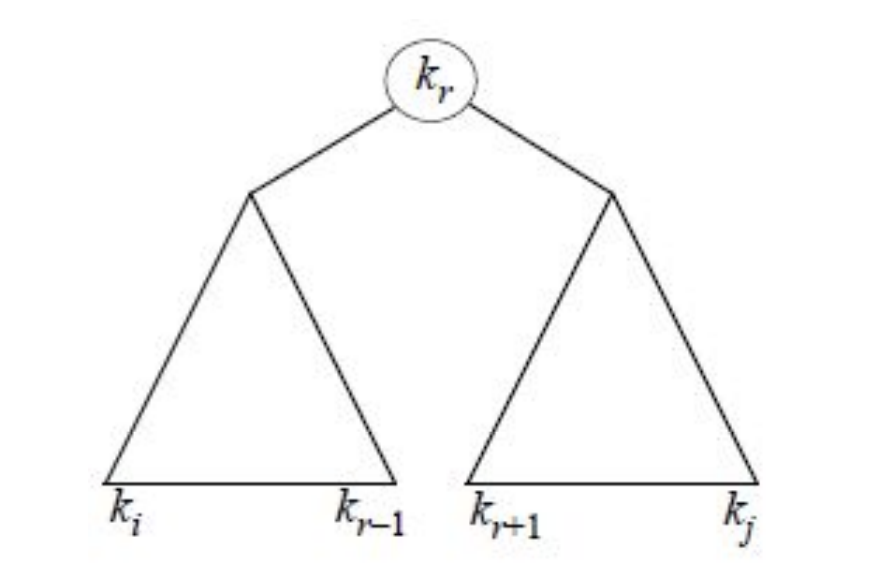
그럼 만약 주어진 가 에서 의 key들이 있다고 한다면, 그 중 어떤 key, 하나로 root node 값을 정하게 되면, 왼쪽 subtree는 의 key들을 포함하게 되고, 오른쪽 subtree는 의 key들을 포함하게 된다. 그럼 인 값에 대해 이진 탐색 트리를 만들게 되고(subproblems로 나누게 되고), 해당 이진 탐색 트리의 기대값을 위에서 구한 공식을 이용하여 계산해나간다면, 만들 수 있는 이진 탐색 트리 중 최적 이진 탐색 트리를 만들 수 있게 된다(optimal solution을 구할 수 있다). 즉, optimal substructure를 가지고 있다!
Step 2
그럼 이제 어떻게 효율적인 방식으로 재귀적으로 subproblems들을 처리할 지 알아보자. 배열 에 기대값들을 저장하며, 에 의 key들을 가지는 최적 이진 탐색 트리의 기대값들을 저장한다. 이 때, 각 값들은 모두 정렬되어 있다고 가정했기 때문에, 이 되는 경우에는 이 된다. 더 이상 key가 없고 dummy key만이 존재할 것이기 때문이다. 그리고 일반적인 경우, 이면, 최적 이진 탐색 트리기 때문에, left subtree의 값과 right subtree의 값에 를 더하면 될 것이다. 여기서 는 다음과 같이 정의된다.
즉, subtree의 key와 dummy key들의 확률의 합이다.
결론적으로 아래와 같이 수식화할 수 있다.
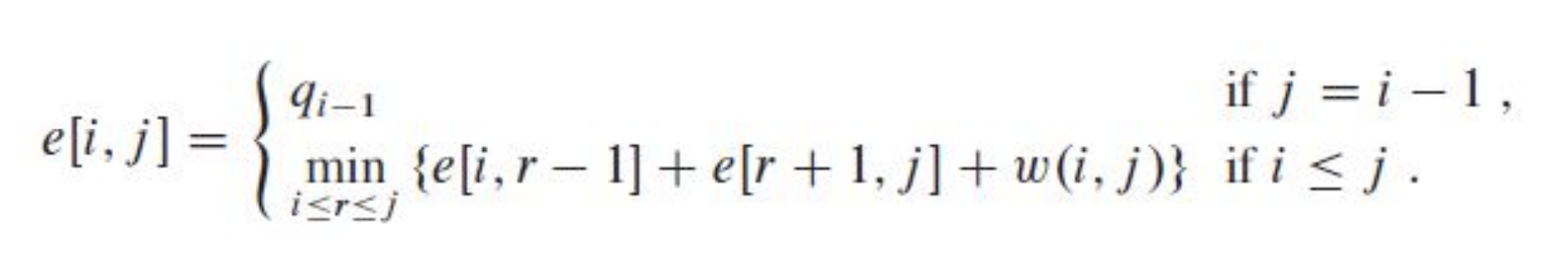
Step 3
이제 optimal solution을 계산해보자. 주어진 에서 어느 값을 root node로 두었는지를 의미하는 값을 저장하는 "root table", 기대값이 확률의 합에 의해 증가하기 때문에, 값을 저장하는 " table", 기대값을 저장하는 " table"을 구성하게 된다. 주어진 input이 아래의 표와 같다면,
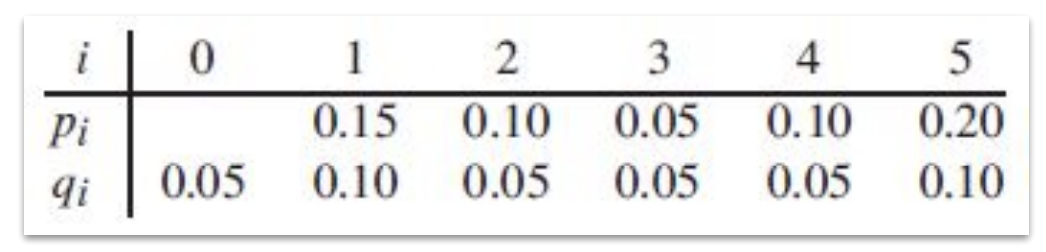
이전 연산 결과를 기록한 table들은 아래와 같다.
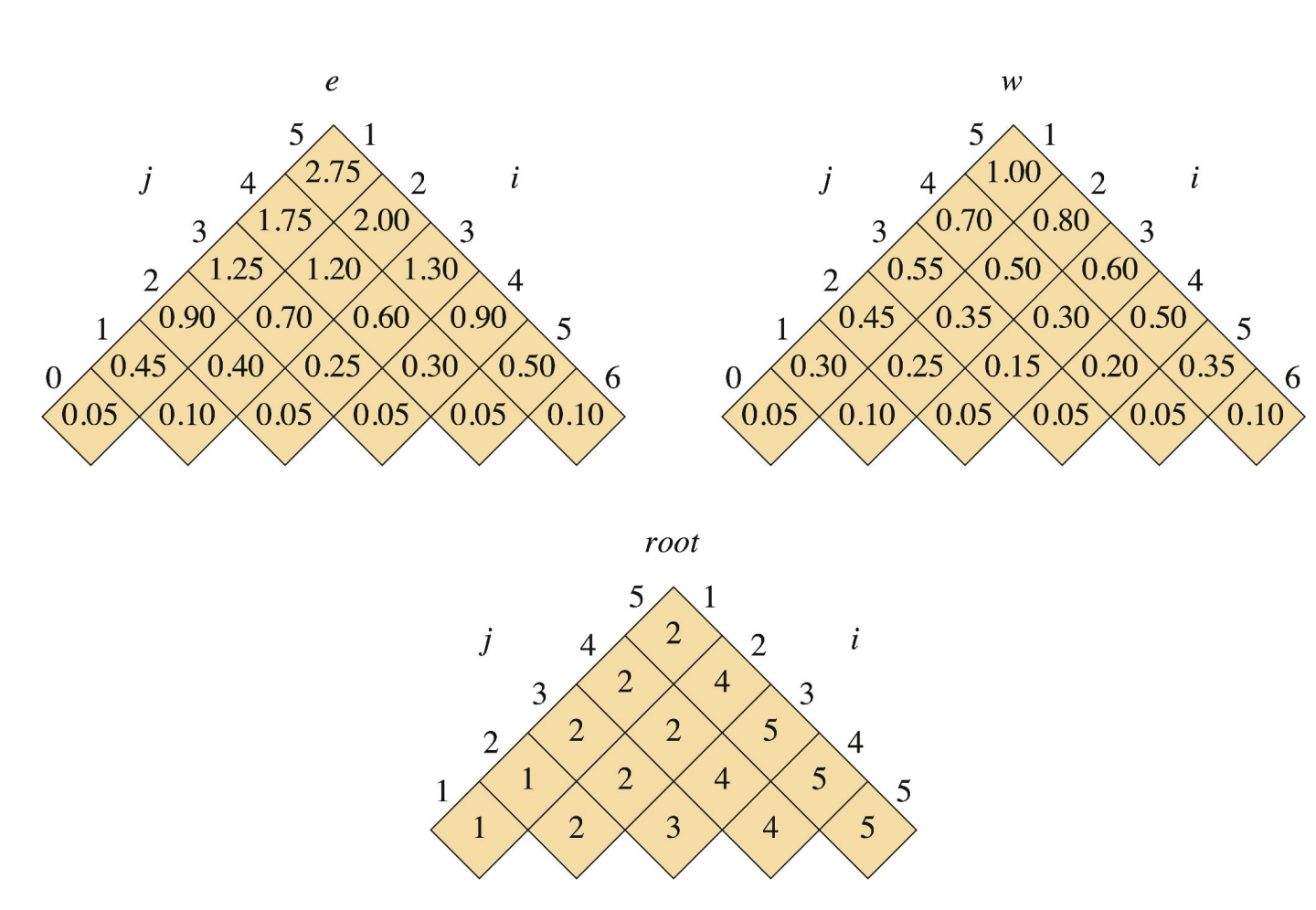
수도 코드는 아래와 같다.

Step 4
위의 연산 결과들을 가지고 optimal solution을 구해보자. root table을 참고하면, 일단 의 root node에는 2가 오게 된다. 그럼 left subtree는 로 아래에는 더 이상 key들이 없고 dummy keys만 존재한다. right subtree는 로 right subtree의 root node는 5가 온다. 그리고 다시 right subtree의 left subsubtree와 right subsubtree로 나누면, 각각 로 right subtree의 left subsubtree의 root node는 4, right subtree의 right subsubtree 더 이상 key들이 존재하지 않는다. 그 후 lef left subsubtree의 left subsubsubtree와 right subsubsubtree를 구해보면 각각 로 root node는 left subsubsubtree는 3, right subsubsubtree는 더 이상 key들이 존재하지 않고, 최적 이진 탐색 트리의 구조를 알 수 있게 된다. 이 최적 이진 탐색 트리의 기대값은 table의 의 값이 될 것이다.(2.75) 말로 설명하자니 상당히 복잡하고, sub를 몇 번 사용했는지 모르겠는데 최종 결과를 그림으로 표현하면 아래와 같다.
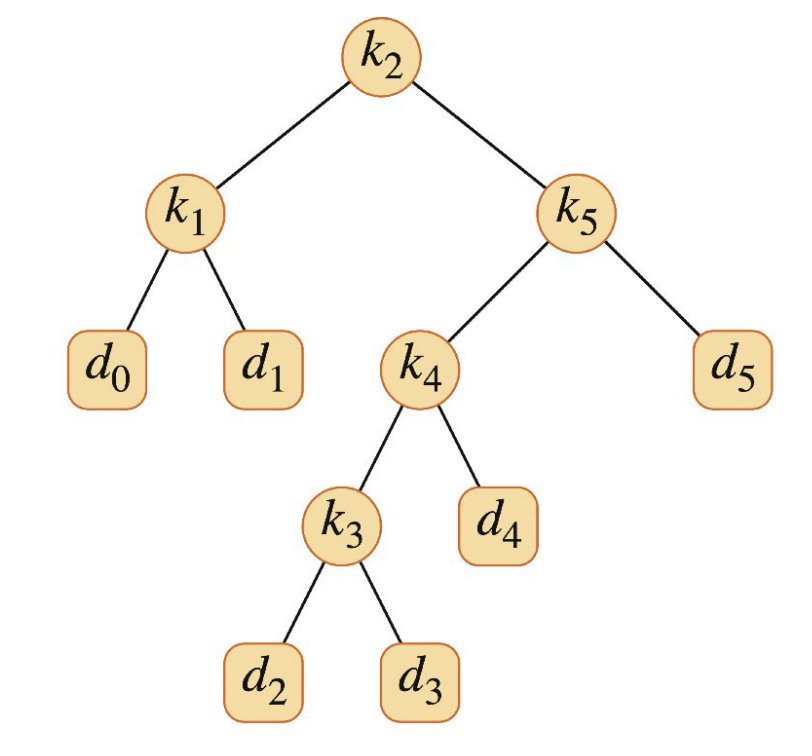

https://velog.io/@eunjilee1111/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%B6%84%ED%95%A0-%EC%A0%95%EB%B3%B5-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98