[알고리즘] 08. Greedy Algorithm (Part 1)

jmt·2024년 4월 13일

알고리즘

목록 보기

9/18

Introduction

지난 시간에 동적 프로그래밍(DP)를 통해 optimal substructure가 있는 최적화 문제(optimizaiton problem)를 어떻게 효율적으로 풀 수 있는지를 배웠다. 완전 탐색(brutue force)이 가장 간단한 방법이지만, 시간 복잡도가 대부분 exponential 하기 때문에, polynomial하게 문제를 풀고 싶었기 때문이다. 그런데, DP 기법을 적용하기 위해서는 추가적인 배열을 선언하여 더 많은 저장공간(메모리)를 요구하고, 특정 배열을 모두 계산하여 채워나가야 하는 과한 면이 있었다. 최적화 문제를 풀기에 더 간단한 알고리즘이 있지 않을까? 하는 의문점에서 시작된 것이 Greedy Algorithm이다. 최적화 문제를 풀기 위해서는 각 단계마다 일련의 선택을 했어야 했다. 그리고 최적의 선택을 하기 위해, DP에서는 사전에 계산해둔 연산 결과를 배열에 저장하여 그 배열을 참조하여 선택을 했었는데, 그냥 현재 시점에서 최선의 선택(Greedy Choice)를 하면 전체적으로 가장 최적의 해가 구해질 것 같다는 생각이 Greedy Algorithm의 기본 concept이다.

Activity Selection

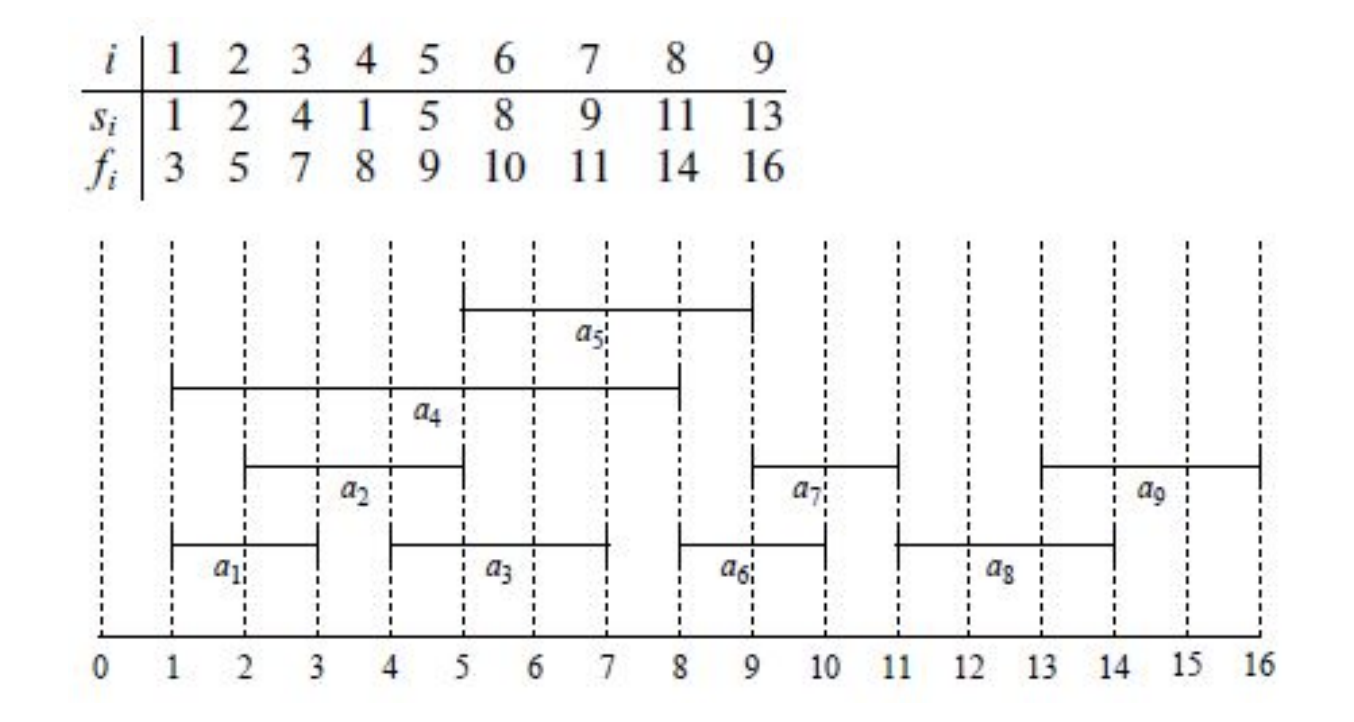
activity selection문제를 통해 Greedy Algorithm을 알아보자. $n$ 개의 활동들을 겹치지 않게 스케쥴링(scheduling)하는 문제를 activity selection이라 한다. 여기서 어떤 활동 $a_i$ 는 자원을 $[s_i,\, f_i)$ 만큼 소모한다. 즉, $a_i$ 는 $s_i$ 부터 $f_i$ 까지 자원을 사용하겠다는 의미이다. 우리는 여기서 모든 활동들이 겹치지 않게 스케쥴링을 해야하고, 가능한 가장 많은 활동들의 집합을 고르면 된다. 다만 여기서 조건은 각 활동들은 $f_i$ 값을 기준으로 오름차순으로 정렬되어 있다고 가정한다. 예를 들어 아래와 같은 예시가 주어졌다고 가정하자.

Optimal Substructure

activity selection 문제의 obtimal substructure가 있는 지 알아보자. 즉, 각 단계에서 최적의 선택이 존재하고, subproblem의 최적의 선택으로 전체 문제의 최적해를 구할 수 있는지 확인해보자. 다음과 같이

S_{ij} = \{a_k \in S : f_i \le s_k < f_k \le s_j \}

를 정의해보자. $S_{ij}$ 는 임의의 활동 $a_i$ 와 $a_j$ 사이에 존재하는 활동들의 집합이다. $S_{ij}$ 에서 겹치지 않는 최대 크기의 집합(maximum-size set)을 $A_{ij}$ 라 정의하자. $A_{ij}$ 안에 있는 활동들을 $a_k$ 라고 하면, $S_{ij}$ 를 두 개의 subproblems( $S_{ik},\; S_{kj}$ )로 나눌 수 있게 된다. 이제 $S_{ik}$ 와 $S_{kj}$ 에서 겹치지 않게끔 활동들을 선택하면 된다.(= $A_{ik}, A_{kj}$ 를 찾으면 된다.) 그런데, $A_{ik}$ 는 $A_{ij}$ 에서 $a_k$ 가 시작하기 이전에 끝나는 작업들을 포함하게 되고, $A_{kj}$ 는 $A_{ij}$ 에서 $a_k$ 가 끝난 뒤 시작하는 작업들을 포함하게 된다. 그럼,

\begin{aligned} A_{ij} = A_{ik} \cup \{a_{k}\} \cup A_{kj}\\ \Rightarrow |A_{ij}| = |A_{ik}| + |A_{kj}| + 1 \end{aligned}

이므로, activity selection 문제는 optimal substructure를 가진다는 것이 확인되었다. 그렇다면, 최적해가 두 개의 subproblems에 대한 최적해를 포함하는가? 즉, 최적해 $A_{ij}$ 가 $S_{ik},\, S_{kj}$ 의 최적해를 포함하는지 확인해보자.

이는 모순을 보임으로 증명 가능하다. 만약, $|A_{kj}|$ 보다 큰 $|A^{\prime}_{kj}|$ 가 존재한다고 하자. 그럼,

|A_{ik}| + |A^{\prime}_{kj}| + 1 > |A_{ik}| + |A_{kj}| + 1

가 된다. 하지만, $A_{ij}$ 가 최적이라는 가정에 위반되기에 모순이다.

Recursive Solution

dynamic programming으로 풀려면, 배열 $c$ 를 정의하여, $S_{ij}$ 의 최적해의 크기를 저장하는 $c[i,\,j]$ 에 저장된다. 이는 다음과 같은 수식으로 재귀호출되며 저장될 것이다.

c[i\; j] = \begin{cases} 0 &\text{if }S_{ij}= \empty\\ \max_{a_k \in S_{ij}}\{c[i,k]+c[k,j]+1\}&\text{if }S_{ij}\neq \empty \end{cases}

Greedy Choice

하지만 모든 subproblems을 푸는 DP기법이 아닌 Greedy Algorithm으로 풀고 싶다. 그렇다면 Greedy Choice가 가능한 지 확인해보자. activity selection에서 Greedy Choice는 "제일 먼저 끝나는 activity"가 된다. 그 이유는 빨리 끝나는 활동을 선택해야, 남은 자원에 더 많은 활동들을 할당할 수 있기 때문이다.

그전에 subproblem 하나를 풀기 위해 집합 표현을 간략화하자.

S_k = \{a_i \in S : s_i \ge f_k \}

$S_k$ 에는 $a_k$ 가 끝난 이후 시작하는 모든 활동들을 포함하게 된다. 만약 $a_1$ 이 가장 빨리 끝나는 활동이라 greedy choice(optimal solution)를 했다면, 우리는 $S_1$ 중에서 가장 빨리 끝나는 활동을 골라서 optimal solution을 고를 수 있다.

그러나, 매 단계의 greedy choice가 항상 최적의 해의 일부가 되는가?

Theorem

만약, $S_k$ 가 비어있지 않고, $a_m$ 이 $S_k$ 중에 가장 먼저 빨리 끝난다면, $a_m$ 은 optimal solution에 포함된다.

Proof

$A_k$ 가 $S_k$ 의 최적해라고 하자. $A_k$ 안에 가장 빨리 끝나는 활동 $a_j$ 를 $A_k$ 에서 제외하고 가장 빨리 끝나는 활동 $a_m$ 을 넣는다 하고 이 최적해를 $A^{\prime}_k$ 라고 하자. 만약 $a_j$ 와 $a_m$ 이 같다면, 기존과 동일하기 때문에 주장은 타당하다. 하지만 만약 그렇지 않다면,

A^{\prime}_{k} = A_k - {a_j} \cup {a_m}

이 된다. 그런데 $A^{\prime}_k$ 에는 겹치지 않는 활동들만 가지고 있다. 그렇기 때문에, $|A^{\prime}_k| = |A_k|$ 이다. 그러므로 $A^{\prime}_k$ 도 $S_k$ 의 최적의 해가 될 수 있으므로, 가장 빨리 끝내는 greedy choice가 최적의 해의 일부가 됨이 증명되었다.