0. Abstract

• 기존 LLM은 Left-To-Right, Token-Level decision Process 방식에 국한되어 있음.
• 탐구, 전략적 예측, 초기 결정의 영향이 큰 task에 대해 부족함이 있음.
• 위 문제들을 해결하기 위해 ToT를 제안
  • coherent unit of thought(text)를 문제를 풀기 위한 중간 step으로 만든 후 탐구
  • ToT를 활용하여 LM이 다양한 추론 방법 경로를 고려하며, self-evaluating하여 next course of action을 결정하기 위한 choices를 할 수 있음.

1. Introduction

사람이 의사결정을 하는데 있어서 2가지 모드를 사용.

System 1. fast & automatic, unconscious mode

System 2. slow & deliberate, conscious mode

이 2가지 모드는 machine learning에 사용되는 다양한 수학적 모델과 연결되어 있음.

System 1 : the simple associative token-level choices

System 2 : evaluates its current status and actively looks ahead or backtracks to make more global decisions

논문에서는 planning process를 디자인 하기 위해 Tree of Thoughts를 제안함.

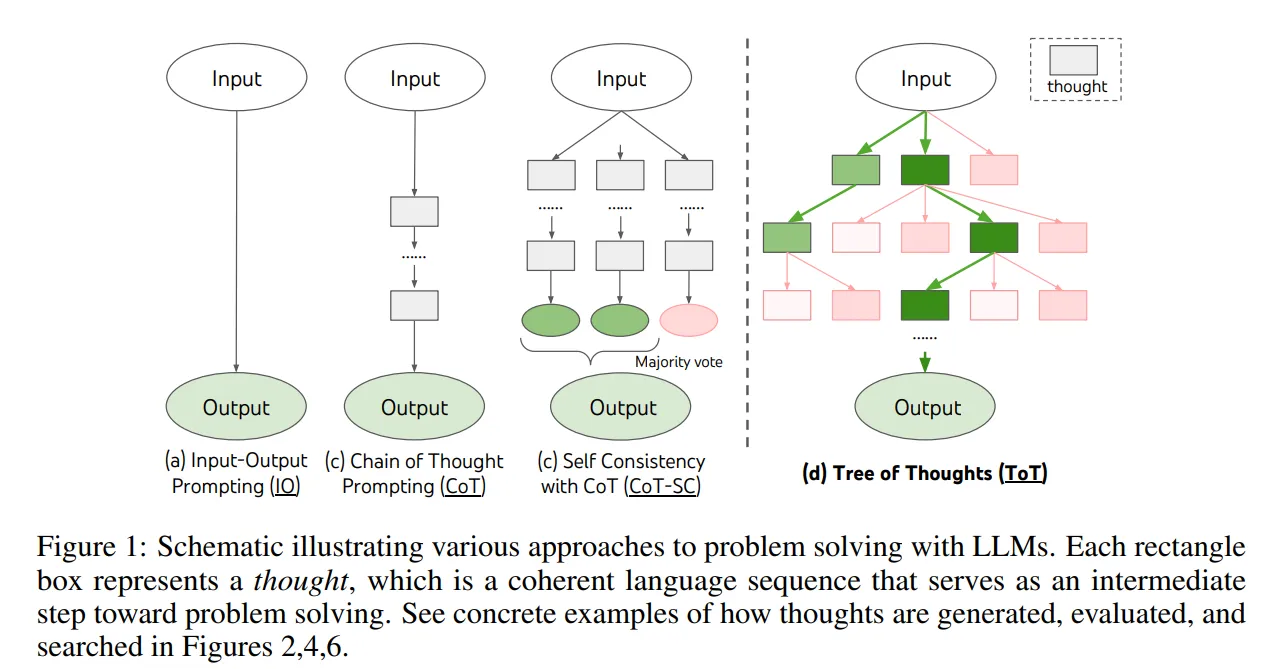
thought : 문제 해결을 위한 intermediate step 역할을 하는 coherent language sequence.

high-level semantic unit을 통해 LM은 deliberate reasoning process를 통해 문제 해결을 위한 different intermediate thought의 progress를 self-evaluate할 수 있음.

laguage-based capability를 결합하여 search algorithms(BFS, DFS)을 통해 thoughts를 생성하고 평가하여 lookahead와 backtracking을 통해 ToT를 체계적으로 탐구할 수 있음.

Task

1. Game of 24
2. Creative Writing
3. Crosswords

연역적, 수학적, 기본 상식, 어휘 추론 능력, 체계적 계획 세우기 또는 검색을 필요로 하는 task.

2. Background

$p_ \theta$ = pre-trained LM with parameter $\theta$

$x, y, z, s, ...$ : language sequence

$pθ(x) = \Pi ^n_{i=1} pθ(x[i]|x[1...i])$- $x[i]$ is a token

uppercase letter S, … : collection of language sequences.

Input-output prompting

문제를 해결하는 가장 흔한 방법으로 input $x$를 넣으면 output $y$를 내보내는 방식

LM : $y$ ~ $p_\theta(y|prompt_{IO}(x))$ - $prompt_{IO}(x)$는 task instructions 와/또는 few-shot input-output examples로 구성.

Chain-of-thought prompting

input $x$가 output $y$로 매핑되는 것이 중요하지 않은 문제를 해결하기 위해 만들어진 방법. (예, input $x$는 수학 질의 output $y$ 는 수치 답인 경우)

CoT($z_1, ...,z_n$)는 $x$와$y$ 를 잇기 위한 방법으로 각 $z_i$는 문제 해결을 위해 meaningful한 intermediate step의 coherent language sequence이다. (math QA에서 intermediate equation같은 걸로 볼 수 있음)

각각의 thought는 $z_i$ ~ $p^{CoT}_\theta (z_i|x, z_{1...i-1})$는 순차적으로 샘플링 된 다음 output으로 $y$ ~ $p^{CoT}_\theta (y|x, z_{1...n})$ 나옴.

Self-consistency with CoT

CoT를 ensemble하는 방식으로 k개의 서로 다른 CoT를 샘플링 : $[z^{(i)}_{1...n}, y^{(i)}]$ ~ $p^{CoT}_\theta(z_1...n, y|x)$($i = 1 ... k)$, 그 다음 가장 빈번한 출력을 반환: $argmax_y$ ≠ {${i|y^{i} = y}$}.

CoT를 개선시킨 method로 같은 문제를 해결하는 데에는 여러 가지 서로 다른 output decision이 있을 것이라는 아이디어에서 착안.

더 풍부한 thoughts set을 탐색함으로써 output decision이 더 faithful할 수 있음.

3. Tree of Thoughts : Deliberate Problem Solving with LM

Research on human problem-solving suggests that people search through a combinatorial problemspace – a tree where the nodes represent partial solutions, and the branches correspond to operators that modify them

This perspective highlights two key shortcomings of existing approaches that use LMs to solve general problems

1. Locally : they do not explore different continuations within a thought process – the branches of the tree
2. Globally : they do not incorporate any type of planning, lookahead, or backtracking to help evaluate these different options – the kind of heuristic-guided search

위 문제점들을 해결하기 위해 LM이 thought reasoning path를 탐구할 수 있도록 허락해주는 ToT를 제안. ToT는 모든 문제를 search over a tree로 구성

$state s = [x, z_{1...i}]$로 thought의 input과 sequence와 함께 partial solution을 나타냄.

ToT의 specific instantiation은 4가지 질문에 대답하는 것을 포함.

1. How to decompose the intermediate process into thought steps

   • Thought decomposition

   CoT는 coherently하게 thoughts를 샘플링하는 반면에, ToT는 문제 속성(problem properties)를 활용하여 intermediate thought steps를 설계하고 분해함.

   일반적으로 thoughts는 LM이 promising하고 diverse한 sample을 생성할 수 있도록 작아야 하지만 LM이 예측을 평가할 수 있도록 커야함.

2. How to generate potential thoughts from each state

   • Thought generator $G(p_\theta, s, k)$

   Given a tree state $s = [x, z_1...i]$. we consider two strategies to generate $k$ candidates for the next thought step:

   • Sample
   • thoughts from a CoT prompt (Creative Writing): $z^{(j)}$ ~ $p^{CoT}_\theta (Z_{i+1}|s) = p^{CoT}_\theta(Z_{i+1}|x, z_{1...i}) (j=1...k)$

   이 작업은 thought space가 풍부하게 있어야 잘 됨.

   • Propose

     • thoughts sequentially using a “propose prompt” (Game of 24; Crosswords): $[z^{(1)},..., z^{(k)}]$~$p^{propose}_\theta(z^{(1...k)}_{i+1}|s)$

       이 작업은 thought space가 제한적일 때 잘 작동되며, 동일한 맥락에서 다른 thoughts를 제안하면 중복을 방지함.

3. How to heuristically evaluate states

   • State evaluator $V(p_\theta, S)$

   서로 다른 states의 변경이 주어지면, state evaluator가 문제 해결을 위한 과정을 평가. 휴리스틱은 검색 문제를 해결하기 위한 일반적인 방법이었지만, 이들은 일반적으로 프로그래밍 되어 있거나 학습되어 있음.

   논문에서는 LM을 사용하여 state에 대해 deliberately reason 함으로써 3번째 대안을 제시.

   deliberate heuristic은 프로그래밍 규칙보다 flexible하고 학습 모델보다 sample-efficient함.

   논문에서는 thought generator와 유사하게 state를 either independently or together로 평가하는 2가지 전략을 제시.

   • Value each state independently : $V(p_\theta, S)(s)$ ~ $p^{value}_\theta(v|s) \forall s \isin S$ 여기서 value prompt는 state $s$가 scalar value $v$를 생성하는 것에 대한 추론.
     • Game24, Crosswords에 적용
   • Vote across states : $V(p_\theta, S)(s) = 1[s = s^*]$ 성공 여부를 바로 평가하기 어려운 경우에 사용
     • Creative Writing에 적용

4. What search algorithm to use

   • Search algorithm. BFS와 DFS를 사용
     

   

   4.1 Game of 24

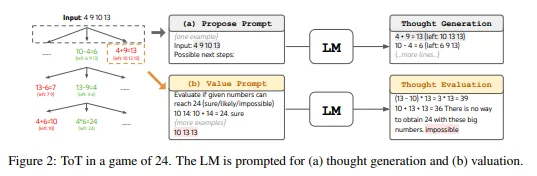
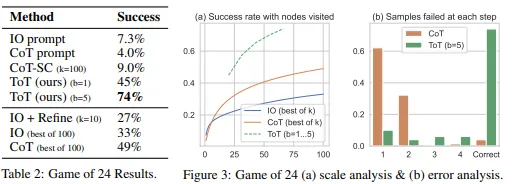
4.2 Creative writing

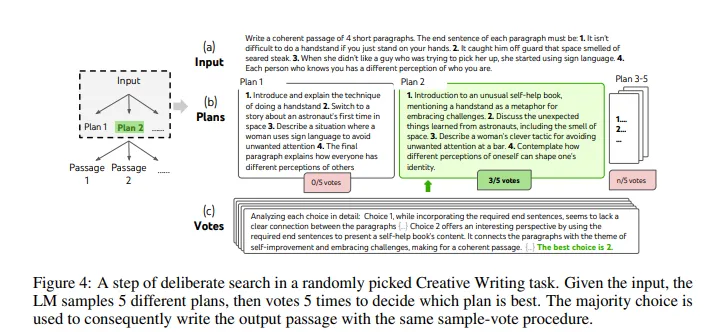
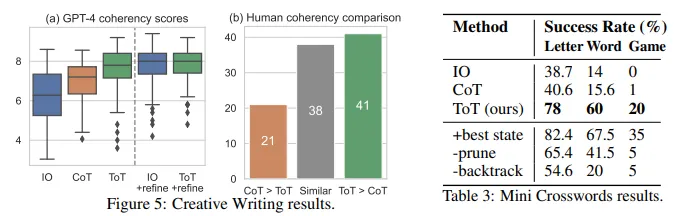
4.3 Mini crosswords

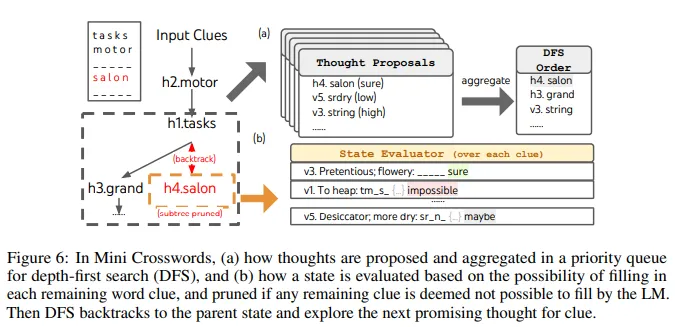
5. Related Work

• Planning and decision making
• Self-reflection
• Program-guided LLM generation
• Classical search methods