4.5 유용한 특성 선택
과대적합(overfitting) : 훈련 세트에 너무 가깝게 맞춰진 샘플
과대적합을 벗어나는 방법은 대표적으로 아래와 같은 방법들이 있다.
- 더 많은 훈련 세트를 준비
- 규제(regularization)를 활용해 복잡도 제한
- 더 간단한 모델 사용
- 차원 축소
4.5.1 L1, L2 규제 (Regularization)
L1은 희소한 특성 벡터를 만든다.
-> 대부분의 가중치가 w=0이 된다.
->관련 없는 특성이 많은 고차원 데이터의 경우 효과가 좋다.
4.5.2 L2 규제의 기하학적 해석
-> weight가 너무 커지지 않도록 한다.
2차원으로 본 L2 규제
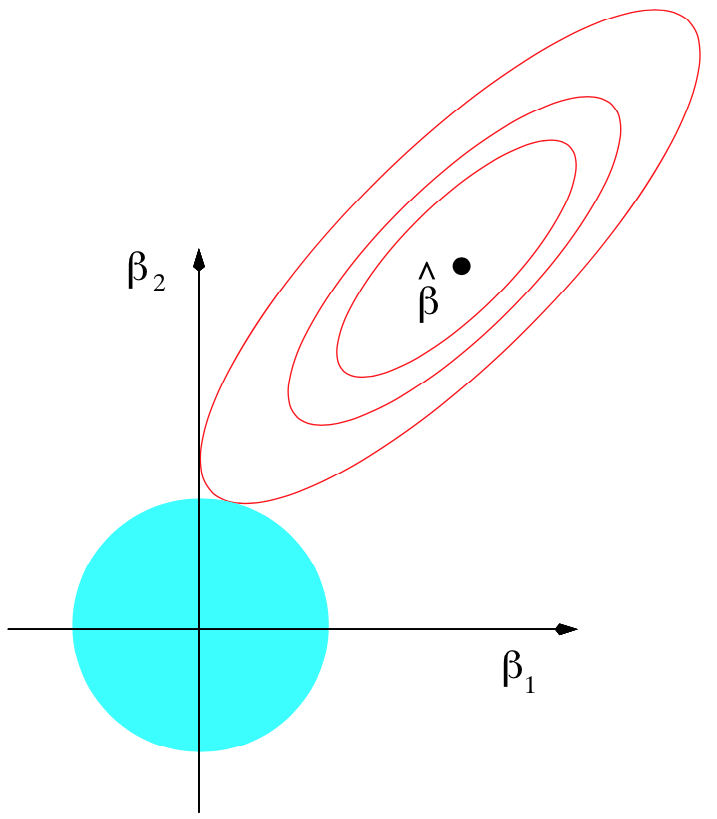
- 로 생각하면 된다.
파란 원 부분이 규제, 타원형 등고선이 오차 함수이다. 타원의 가운데 부분이 최소값이다. 저기에 도달하면 훈련세트에 대해서 오차가 최소가 되도록 하는 점이다. 하지만 이 경우 모델이 과적합 될 수 있다. 이를 방지하고자 원과 접하는 점까지만 오차를 최소화 한다.
3차원으로 본 L2 규제
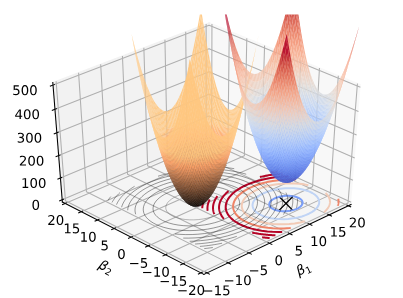
3차원으로 보면 이렇게 둘 다 그물 모양이다.
식을 간단하게 생각해보면
j=2까지만 해서 생각해보면 어디서 많이 본 식이다. 바로 중학교때 배운 원의 방정식이다. 그래서 원이 된다. 위의 3차원 그래프도 변수 2개인 상황에서 상상할 수 있는 그림이다. 이 이상의 변수에서는 시각화 할 수 없기 때문에 여기까지만 눈으로 확인하도록 하자
4.5.3 L1 규제를 사용한 희소성
L2와 분리된 그림을 찾지 못했다..ㅠㅠ 이렇게 된 김에 둘을 비교해서 생각해보자. 둘의 모양이 다른 이유는 식의 차이에서 알 수 있다. 절댓값이 들어가는 모양이라 마름모 모양이 나온다.
두 규제의 가장 큰 차이라고 하면 L2 규제는 접하는 부분의 w값을 선택하는데 비해 L1은 꼭지점에서만 값을 선택하게 된다. 이 결과 특정 w값이 0이 되게 되면서 유용하지 않은 특성을 걸러내는 효과를 갖게 된다.
4.5.4 순차 특성 선택 알고리즘
과대적합을 피하는 방법으로는 차원 축소 방법이 있다. 이 방법은 규제가 없는 모델에서 유용하다.
차원 축소에는 또 두 가지 방법이 있다.
1. 특성 선택, feature selection
2. 특성 추출, feature extraction
특성 추출은 5장에서 알아보도록 하고 여기서는 전통적인 방법인 특성 선택 방법을 알아보도록 하자.
순차 특성 선택(Sequential Feature Selection)
greed search algorithm으로 특성을 선택한다. greed search는 각 단계에서 최고의 선택을 반복하는 방법이다.
전체 d차원 중에서 k차원으로 축소한다.
exhaustive search algorithm
완전 선택 알고리즘은 greed search와 반대의 알고리즘이다. 모든 경우의 수를 다 탐색하는 알고리즘이다.
순차 후진 선택(Sequential Backward Selection, SBS)
- 과대 적합 모델의 경우 예측 성능이 올라갈 수 있다.
- k=d, 즉, 최대 차원에서 알고리즘이 시작한다.
- 를 최대화하는 특성 을 결정한다.
- 쉽게 말해서 뺐을때 성능이 제일 좋아지는 특성을 말한다.
- 제거
- 특성수가 k개가 되면 알고리즘을 종료한다.
Random Forest Feature Importance
앙상블에 참여한 모든 결정트리에서 계산한 평균적인 불순도 감소로 특성 중요도 측정
랜덤포래스트를 활용하는 방법은 선형적인 구분이 가능한 데이터셋에서만 효과가 있다.
랜덤 포래스트는 두 특성의 상관계수가 높으면 하나의 특성은 정보를 완전히 잡지 못 할 수 있다.
왜냐하면 상관성이 높은 하나의 특성으로 분류했을때 다른 특성 역시 이미 분류가 잘 되었을 가능성이 높기 떄문이다.
