5.1 PCA를 통한 비지도 차원축소

5.1.1 PCA 주요 단계

PCA란?

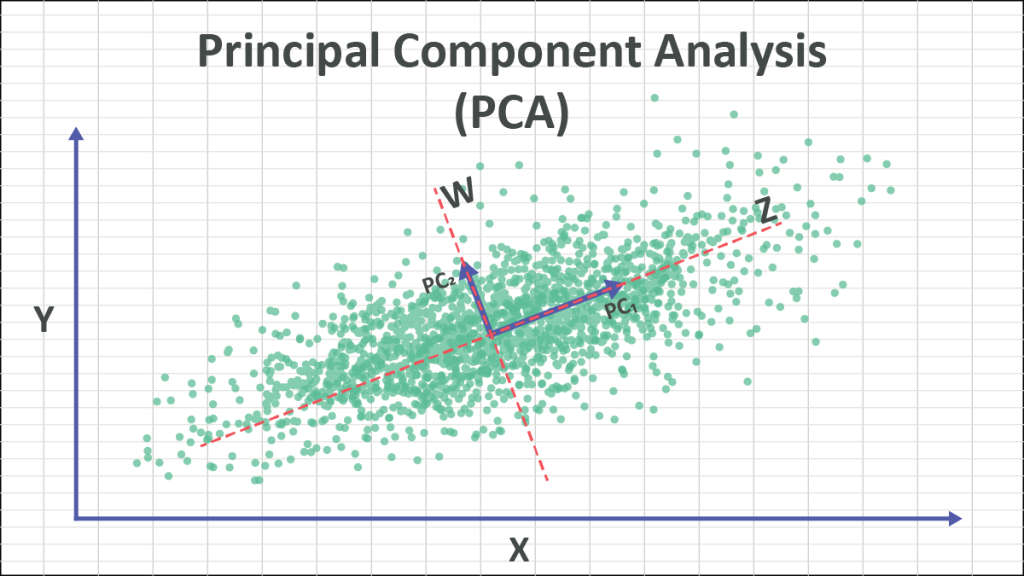
EDA, Denoising 등에서 활용가능한 차원 축소 방법

pca는 상관관계 기반 패턴 찾기 방법이다.
=> 분산이 가장 큰 방향을 찾는다.
-> 구분이 잘 되는 방향을 찾는다.
-> 설명력이 높은 방향을 찾는다.

위 그림을 바탕으로 설명하기에 앞서 분산에 대해서 생가해보자.

※분산이란?
먼저 분산은 뭘까? 어렵게 생각할 필요 없다. 넓게 펼쳐진 정도를 말한다. 이를 수치적으로 말하지 않아도 상관없다. 그럼 넓게 펼쳐진 정도가 왜 중요할까?

어떤 방향으로 넓게 펼쳐졌다는 것은 해당 특성에서 데이터간의 차이가 많이 난다는 뜻이다. 예를들어 생각해보자. 한국인의 평균 월급이 300만원이라고 가정해보자. 이때 분산이 아주 작아서 모든 한국인의 월급이 280~320 사이에 몰려있다고 하자. 그랬을때 과연 사람들 사이에서 월급이 큰 의미가 있을까? 아마 사람들은 다 너도나도 수입이 다 거기서 거기라고 생각할 것이다. 하지만 반대로 평균 월급은 300이지만 0 ~ 1000만원 까지 아주 다양하고 넓게 수입이 분포한다고 생각해보자. 이렇게 되면 사람들간의 수입이 의미하는 바가 이전보다 커지게 된다. 분산이란 이런 개념이다.

이어서 위 그림을 바탕으로 PCA의 의미에 대해서 생각해보자. 분산의 의미를 중심으로 놓고 봤을때 위 그림의 데이터를 x축 혹은 y축으로 표현하는것 보다 z축으로 표현하는것이 가장 큰 의미를 가질 것이다. 그런데 z는 원래는 없던 특성이다. 현실에 존재하는지도 모르는 특성일 것이다. 새로운 차원으로 변환하여 데이터를 설명하는 것이 바로 PCA 이다.

이해하기 어렵다면 예를들어 생각해보자. 위 그림에서 x는 수입 y는 키라고 하자. 위 그림은 사람들을 설명할때 키와 수입으로 설명하려고하는 그림인 것이다.(아주 무자비하고 정없는 설명이지만 일단 무시하기로 한다.) 키와 수입으로도 어느정도 설명이 되고 있지만 훨씬 더 잘 설명할 수 있는 뭔가가 있을것 같다. 이때 Z축은 키와 수입의 조합으로 만들어진 어느 가상의 특성이다. 이 가상의 특성 Z를 통해 사람들을 설명하려고하니 그 차이가 훨씬 두드러 진다. Z값이 큰사람들과 작은 사람들의 차이는 엄청나게 나며 겹치는 사람도 이전보다 적다. 이제는 Z만으로도 충분이 사람들을 가르고 분류할 수 있을것만 같다.

여기서 핵심은 "이제는 Z만으로도 충분이 사람들을 가르고 분류할 수 있을것만 같다."이 부분이다. 우리는 잠시 길을 잃은듯 했지만 차원을 축소하기 위해 PCA를 진행한다. 두 개의 특성으로 표현하니까 뭔가 너무 복잡한것 같다는 느낌이들고 학습이 잘 안되는 기분이다. x만 가지고 설명하자니 뭔가 부족하다. y는 더더욱... 그래서 만들어 낸 것이다 Z축이다.

PCA 순서

1. d차워의 데이터셋을 표준화한다.
2. 공분산 행렬을 만든다.
3. 공분산 행렬의 고유벡터와 고유값을 분해 한다.
4. 고유값을 내림차순으로 정렬한다.
5. 앞에서 k개의 고유벡터를 선택한다. -> 새로운 k개의 기저가 된다.
6. $\textbf{X} \cdot \textbf{W}$를 계산하여 데이터들을 새로운 공간으로 이주 시킨다.

갑자기 어려운 용어들이 많이 나왔다. 하나 하나 뜯어서 생각해보자.

먼저 1번의 d차원의 데이터셋은 최초의 특성이 d개인 데이터들을 말한다.

공분산이란?

$\sigma_{jk} = \frac{1}{n-1} \Sigma^{n}_{i=1} (x^{(i)}_{j} - \mu_{j}) (x^{(i)}_{k} - \mu_{k})$

공분산은 j,k번 째 축을 같이 봤을때 두 개의 대각선 방향으로 얼마나 퍼져있냐는 것을 의미한다. 다시 맨 처음 그림으로 봤을때 데이터들의 중점(그림에서는 붉은색 점선으로 중심을 딱 짚어주고 있다)으로부터 데이터들이 얼마나 퍼져있는가이다. (1/n-1은 PCA개념에서 중요한 것은 아니므로 일단 신경쓰지 않기로 하자.)

이렇게 시그마를 j와k에 대해서 모두 구하여 이를 행렬로 만들면 아랴와 같이 표현된다.

$\Sigma = \begin{bmatrix}\sigma_{1}^2&\sigma_{12}\\\sigma_{21}&\sigma_{2}^2\\ \end{bmatrix}$

이제 이 공분산 행렬의 고유값과 고유벡터를 구해보자.

고유값과 고유벡터란?

여기서 고유값과 고유벡터에 대해서 설명하자면 또 한참을 복잡한 이야기를 해야하기 때문에 간단하게 개념만 잡고 넘어가자.

$\Sigma \vec{v} = \lambda \vec{v}$ (그래도 기본 식은 보고 가자.)

먼저 고유벡터(eigen vector)는 위 식에서 $\vec{v}$를 말한다. 어떤 행렬을 통해 원래의 공간에서 다른 공간으로 변화되었을때도 방향이 그대로인 벡터를 말한다. 쉽게 말하면 두 개의 관점에서 모두 같은 방향을 보는 벡터를 말한다.

그럼 고유값은 무엇인가? 고유 벡터의 방향은 그대로이지만 크기는 그대로가 아닐 수 있다. 이때 크기를 조정해주는 배수값이 고유값이다.

둘을 종합해서 생각해보면 원래의 차원에서도 있는 벡터값이 변화된 곳에서도 같은 방향을 유지하고 있는데 변화된 곳에서는 그 크기가 다 다르다. 즉, 중요도가 달라진다.

그래서 공분산이랑 무슨 상관인데?

다시 원점으로 돌아가 보자. 우린 공분산 행렬을 구하고 그 공분산 행렬의 고유벡터와 고유값을 구했다.

고유 벡터는 원래 데이터 공간에서도 공분산의 공간에서도 방향이 같은 값이다. 즉, 둘 모두의 관점에서 존재하는 값이다. 그런데 고유값에 의해서 그 중요도가 정해졌다. 우리는 4번에서 고유값으로 내림차순으로 정렬을 했다. 우리가 축소하고 싶은 k차원만큼 고유 벡터를 고른다. 고유벡터는 원래 차원에 존재하던 벡터이니까 d차원일것이다. d차원의 벡터를 k개 골랐다. 이를 연결하면 dxk차원의 행렬이 된다.

$\vec{X} \cdot \vec{W}$의 의미는 d차원인 X에 W(dxk)를 곱해서 k차원으로 사영시키는 것이다.

설명된 분산 비율
$\frac{\lambda_j}{sum(\lambda)}$
전체 고윳값에서 각각의 고유값의 비율이다. 고유 값이 클수록 그 비율이 커질 것이다.
이 비율이 각 고유벡터 즉, 변환된 새로운 설명축이 이전의 데이터 공간을 얼마나 대변해서 설명하는지 알 수 있다.

후기

대학시절에 분명히 PCA를 배웠던 적이 있다. 그 때는 너무나도 수식적으로 배워서 도대체 이게 무슨 말인지 하나도 이해하지 못했다. 내가 PCA의 의미를 완전히 이해한건 취업한 후인 최근에 와서다.

오늘의 설명도 충분하지는 않다. 그림자료도 더 많이 사용하고 내가 그려가면서 설명하고 싶은 부분이 한 두가지가 아닌데 너무 귀찮아서 그렇게 하지 못했다. 그런점을 차치하고서러도 좋은 설명이었는지, 또 정확하게 맞는 설명인지는 모르겠다. 많은 지적 부탁드립니다.

참고자료

• https://numxl.com/blogs/principal-component-analysis-pca-101/