Binary Search

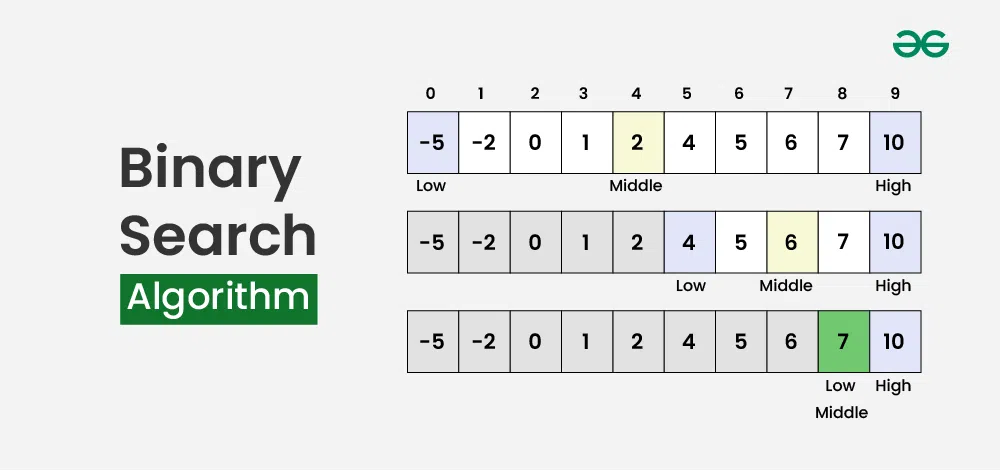
이진 탐색은 정렬된 데이터에서 중간값(mid)을 선택한 후, 목표값과 비교하여 데이터의 절반을 제거하는 방식으로 탐색 범위를 좁혀가는 탐색 알고리즘입니다.

이 과정을 반복하여 목표값을 찾거나, 찾을 수 없는 경우 탐색을 종료합니다.

이진 탐색 과정

---

이미지 출처

1. 중간값 선택: 먼저 배열의 가운데에 있는 값을 선택한다.

2. 값 비교: mid == target이면 해당 index를 반환

3. 왼쪽/오른쪽으로 이동: target이 mid보다 작으면 배열의 왼쪽 부분을 선택하고, 크면 오른쪽 부분을 선택합니다.

4. 과정 반복: mid과 비교하는 과정을 배열이 완전히 분할될 때까지 반복합니다.

구현

---

아래는 c언어로 구현한 이진 탐색 알고리즘입니다.

#include <stdio.h>

int binarySearch(int arr[], int size, int target) {
    int low = 0, high = size - 1;
    
    while (low <= high) {
        int mid = low + (high - low) / 2; // 중간 인덱스 계산
        
        // 중간값이 목표값과 같으면 인덱스를 반환
        if (arr[mid] == target) {
            return mid;
        }
        
        // 목표값이 중간값보다 작으면 왼쪽 부분 탐색
        if (arr[mid] > target) {
            high = mid - 1;
        } 
        // 목표값이 중간값보다 크면 오른쪽 부분 탐색
        else {
            low = mid + 1;
        }
    }
    
    return -1; // 찾지 못한 경우 -1 반환
}

int main() {
    int arr[] = {1, 3, 5, 7, 9, 11, 13};
    int size = sizeof(arr) / sizeof(arr[0]);
    int target = 7;
    
    int result = binarySearch(arr, size, target);
    
    if (result != -1) {
        printf("Element found at index %d\n", result);
    } else {
        printf("Element not found.\n");
    }
    
    return 0;
}

성능평가

---

• 시간 복잡도: $O(\log n)$
  이진 탐색은 매번 탐색 범위를 반으로 줄이기 때문에 시간 복잡도는 로그 시간인 $O(\log n)$입니다.

• 공간 복잡도: $O(1)$
  배열 내에서 직접 탐색하기 때문에 추가적인 공간은 거의 필요하지 않으므로 $O(1)$

장점

---

• 빠른 탐색: 정렬된 데이터가 조건이지만 반씩 덜어내므로 매우 빠른 속도로 찾을 수 있습니다.

• 단순한 구현: 비교적 간단하게 구현할 수 있으며, 재귀나 반복문을 활용할 수 있습니다.

단점

---

• 정렬 필요: 이진 탐색은 배열이 정렬되어 있어야만 적용할 수 있다.

• 데이터 구조의 제약: 배열과 같은 순차 데이터 구조에서만 적용 가능하며, linked list 등에서는 비효율적일 수 있다.

정리

---

이진 탐색은 정렬된 배열에서 매우 효율적인 탐색방법으로, 시간 복잡도가 $O(\log n)$으로 빠르며 비교적 간단하게 구현할 수 있습니다.

하지만 배열이 정렬되어 있어야한다는 조건이 있으며 데이터 구조에 따라 비효율적일 수 있습니다.