Heap Sort

힙 정렬이란

---

자료구조인 heap을 정렬을 기반으로한 정렬 알고리즘으로
max-heaps에서 root node가 가장 큰 값이라는 점을 이용하여 정렬을 수행합니다.

힙 정렬 과정

---

정렬 과정을 그림과 함께 이해하는것이 빠른데
Heap Sort 그림 출처

1. 먼저 array에 있는 값들을 max-heap으로 변환한다.
   

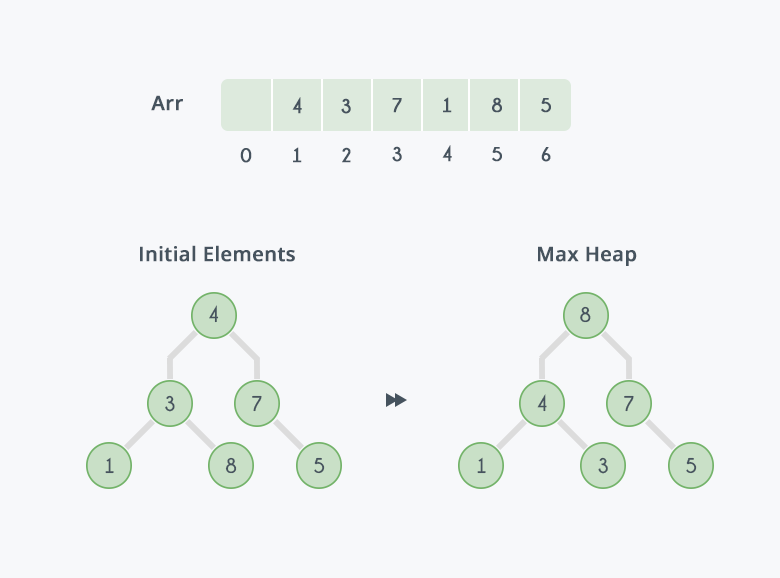
2. step들을 요약하면 root node를 제거하여 배열의 마지막 index로 보내는 것이고 이 과정을 반복하며 정렬이 이루어집니다.

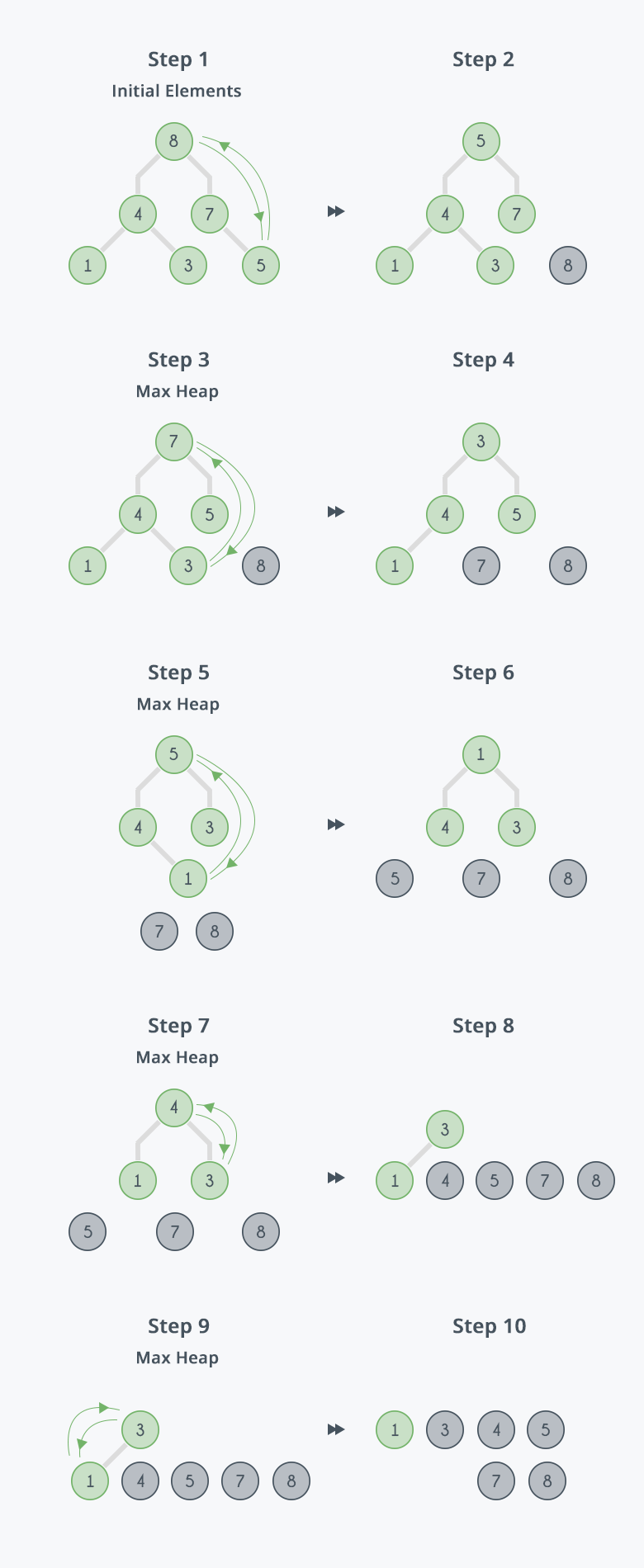
구현

---

다음은 C언어로 구현된 힙 정렬의 코드입니다.

#include <stdio.h>

// To heapify a subtree rooted with node i
// which is an index in arr[].
void heapify(int arr[], int n, int i) {

    // Initialize largest as root
    int largest = i; 

    // left index = 2*i + 1
    int l = 2 * i + 1; 

    // right index = 2*i + 2
    int r = 2 * i + 2;

    // If left child is larger than root
    if (l < n && arr[l] > arr[largest]) {
        largest = l;
    }

    // If right child is larger than largest so far
    if (r < n && arr[r] > arr[largest]) {
        largest = r;
    }

    // If largest is not root
    if (largest != i) {
        int temp = arr[i];
        arr[i] = arr[largest];
        arr[largest] = temp;

        // Recursively heapify the affected sub-tree
        heapify(arr, n, largest);
    }
}

// Main function to do heap sort
void heapSort(int arr[], int n) {

    // Build heap (rearrange array)
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // One by one extract an element from heap
    for (int i = n - 1; i > 0; i--) {

        // Move current root to end
        int temp = arr[0]; 
        arr[0] = arr[i];
        arr[i] = temp;

        // Call max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}

// A utility function to print array of size n
void printArray(int arr[], int n) {
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

// Driver's code
int main() {
    int arr[] = {9, 4, 3, 8, 10, 2, 5}; 
    int n = sizeof(arr) / sizeof(arr[0]);

    heapSort(arr, n);

    printf("Sorted array is \n");
    printArray(arr, n);
    return 0;
}

성능평가

---

힙 정렬의 시간 복잡도를 분석해보면, 삽입과 삭제 각각의 연산은 $O(\log n)$ 이며
전체 데이터의 개수가 $n$개 라면, 이 연산을 $n번$ 반복해야 하므로 총 시간복잡도는 $O(nlon_2n)$ 이다.

장점

---

• 효율적인 시간 복잡도

• 메모리 사용량 : 메모리를 거의 사용하지 않는 제자리 정렬이다.

단점

---

• Costly : 내부적으로 많은 교환 작업을 요구하기 때문에 비용이 많이든다.

• 불안정성 : 기본적인 구현은 안정적이지 않아 동일한 값의 순서가 보장되지 않는다.

• 비효율적인 캐시 사용 : QuickSort와 비교 시 캐시 효율성이 떨어져 속도가 느립니다.

정리

---

• 힙정렬은 제자리 알고리즘이다.
  (자료구조를 추가하지 않고 입력을 변환하는 알고리즘)

• 일반적인 구현이 불안정적이지만 수정으로 안정적으로 만들 수 있다.
  (수정 방법 : taking the position of the elements into consideration.)

• QuickSort보다 보통 2~3배 느린데 이는 힙 정렬이 지역 참조(locality of reference)가 부족하기 때문이다.