Radix Sort

기수 정렬은 숫자를 구성하는 각 자릿수를 기준으로 정렬하는 선형 정렬 알고리즘으로 크기가 고정되어있는 문자나 숫자 정렬에 유용합니다.

기수 정렬의 단계

---

설명을 위해 {170, 45, 75, 90, 803, 24, 2, 66} 라는 배열이 있다고 가정하고

그림 출처

해당 배열에서 자릿수가 가장 큰 값을 확인하고 그 자릿수를 key값으로 정렬합니다.

LSD 방식으로 정렬한다면
먼저 1의자리 숫자를 기준으로 정렬합니다.

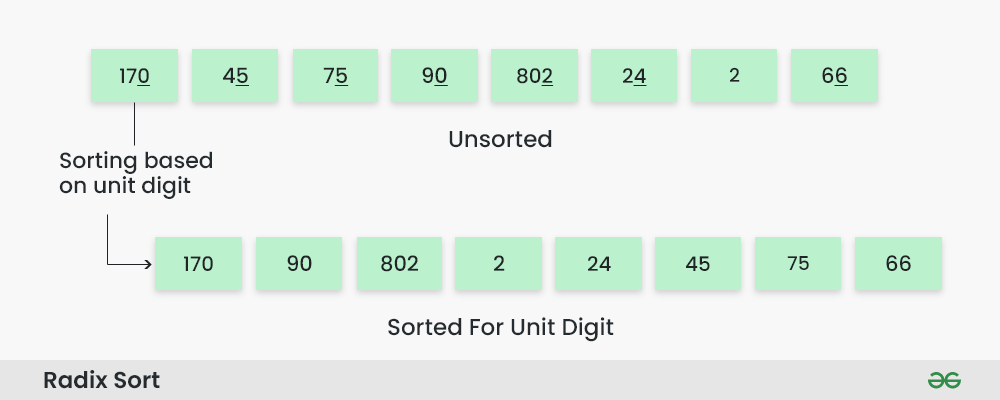
만약 같은 값이 존재한다면 Unsorted 배열에서 우선순위대로 정렬합니다.

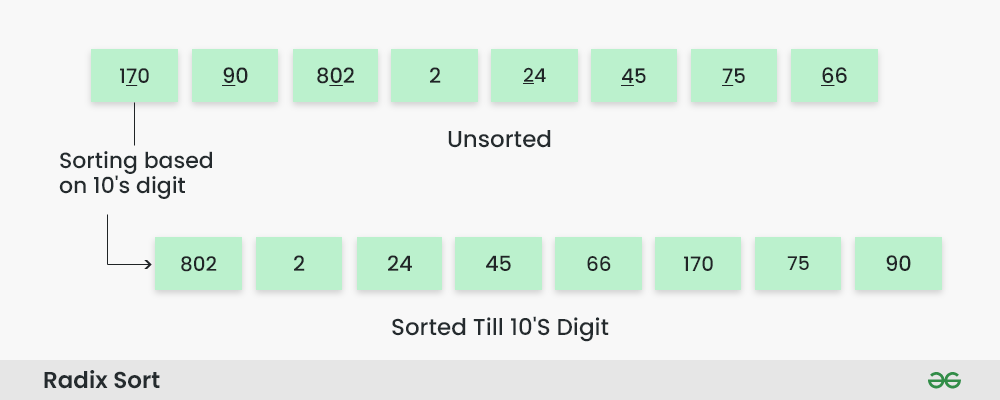
그 다음 10의 자리수로 정렬을하면
(n의 자리 수가없으면 0으로 표시합니다.)

이제 마지막으로 100의 자리 수로 정렬을 진행하면

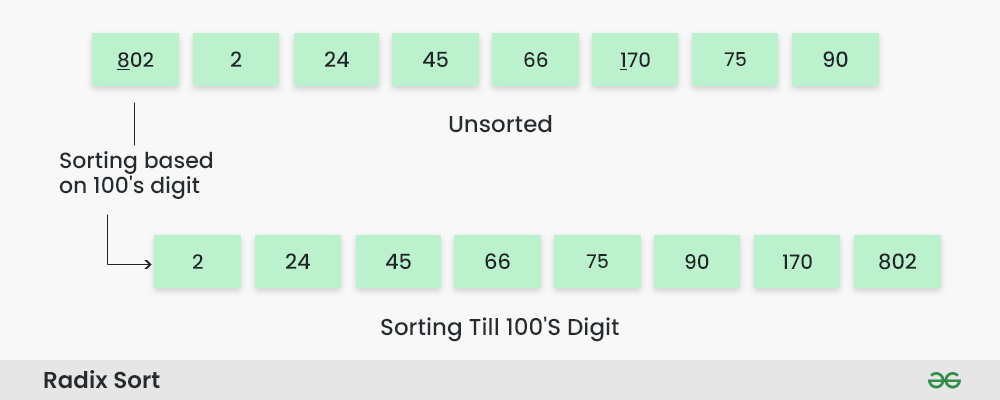
이렇게 오름차순으로 정렬이 됩니다.

기수 정렬 예시 코드

---

c언어로 구현 코드입니다.

#include <stdio.h>
#include <stdlib.h>

#define MAX_NUM 1000000

void countingSort(int arr[], int n, int exp) {
    int output[n];
    int count[10] = {0};

    // Count occurrences of each digit
    for (int i = 0; i < n; i++)
        count[(arr[i] / exp) % 10]++;

    // Calculate cumulative frequencies
    for (int i = 1; i < 10; i++)
        count[i] += count[i - 1];

    // Build output array
    for (int i = n - 1; i >= 0; i--) {
        output[count[(arr[i] / exp) % 10] - 1] = arr[i];
        count[(arr[i] / exp) % 10]--;   

    }

    // Copy output array back to original array
    for (int i = 0; i < n; i++)
        arr[i] = output[i];
}

void radixSort(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; i++)
        if (arr[i] > max)
            max = arr[i];

    // Do counting   
 sort for every digit.
    for (int exp = 1; max / exp > 0; exp *= 10)
        countingSort(arr,   
 n, exp);
}

int main() {
    int arr[] = {170, 45, 75, 90, 802, 24, 2, 66};
    int n = sizeof(arr) / sizeof(arr[0]);

    radixSort(arr, n);

    printf("Sorted   
 array: \n");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");

    return   
 0;
}

성능평가

---

복잡도는 $O((n+b)*log_b(MAX x))$
b는 최대값의 자릿수에 따라 달라집니다.

장점

---

• Fast when the keys are short i.e. when the range of the array elements is less.

• Used in suffix array constuction algorithms like Manber's algorithm and DC3 algorithm.

단점

---

• Since Radix Sort depends on digits or letters, Radix Sort is much less flexible than other sorts. Hence , for every different type of data it needs to be rewritten.

• The constant for Radix sort is greater compared to other sorting algorithms.

• It takes more space compared to Quicksort which is inplace sorting.

정리

---

1. Since Radix Sort depends on digits or letters, Radix Sort is much less flexible than other sorts. Hence , for every different type of data it needs to be rewritten.
2. The constant for Radix sort is greater compared to other sorting algorithms.
3. It takes more space compared to Quicksort which is inplace sorting.