"https://www.geeksforgeeks.org/dsa/introduction-to-red-black-tree/"

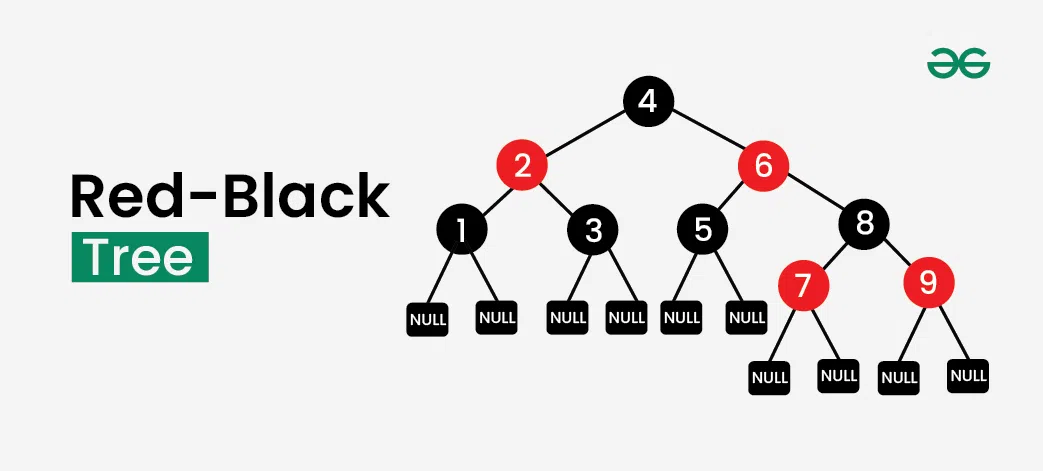
일반적인 이진 검색 트리(BST)는 평균적으로 $O(log N)$의 시간 복잡도를 가지지만, 최악의 경우 편향 트리(한쪽으로 치우침)가 되어 $O(N)$의 성능을 보이는데, RB Tree는 이러한 문제를 해결하여 최악의 경우에도 $O(log N)$을 보장하는 자료구조이다.
(AVL Tree도 있음)

특징(조건)

1. 모든 노드는 검정 혹은 빨강이다.
2. 루트 노드는 검정색이다.
3. 리프(NIL) 노드는 검정색이다.
4. 빨강 노드의 자식 노드는 검정색이다. (빨강 부모, 빨강 자식 불가)
5. 어떤 노드에서 리프(NIL) 노드까지 가는 모든 경로의 검정색 노드 수는 같다. (리프까지 가는 길에서 만나는 검정 노드 수는 같다.)

"https://www.geeksforgeeks.org/dsa/introduction-to-red-black-tree/"

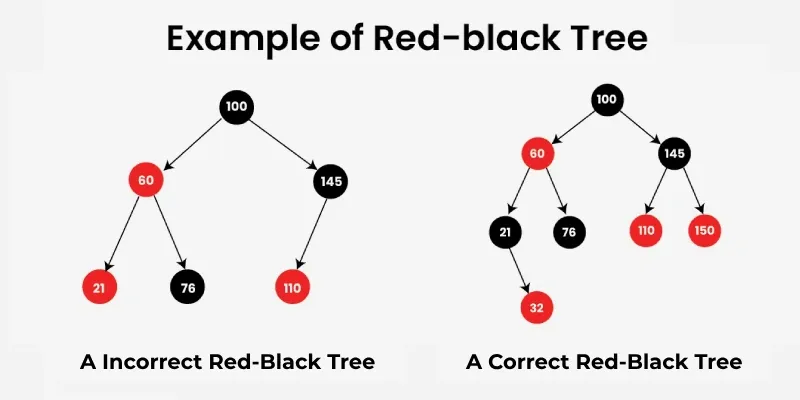
• 위 특징을 만족하는 트리(오른쪽)
• 만족하지 못하는 트리(왼쪽, 60, 21 부모-자식 모두 red 문제)

삽입

• 기본적으로 BST와 같다.
• 삽입하는 노드는 무조건 red

위 삽입 규칙을 따라서 노드를 추가하면 되는데, 여기서 삽입 후 부모노드의 색상에 따라 문제가 발생(Incorrect RB Tree가 되는 경우)한다.

Algorithm [#5-1 Search Tree], Chungbuk National University, School of Computer Science, Prof. Lee, Euijong, 2025 FALL

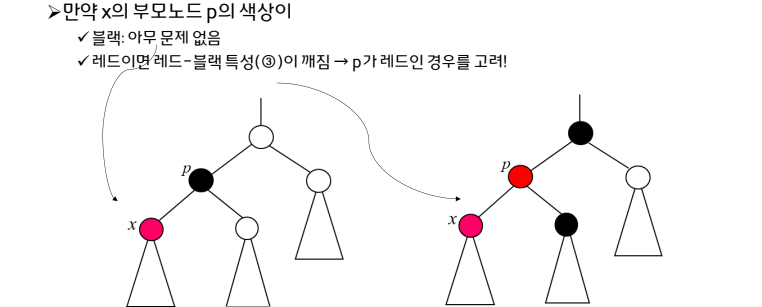
삽입 후 부모노드가 red인 경우

4번째 조건을 위반하는 경우인데 이때 Restructing과 Recoloring으로 해결할 수 있다.
이 두 방법을 사용하는 case는 또 삼촌 노드에 따라 달라진다.

Algorithm [#5-1 Search Tree], Chungbuk National University, School of Computer Science, Prof. Lee, Euijong, 2025 FALL

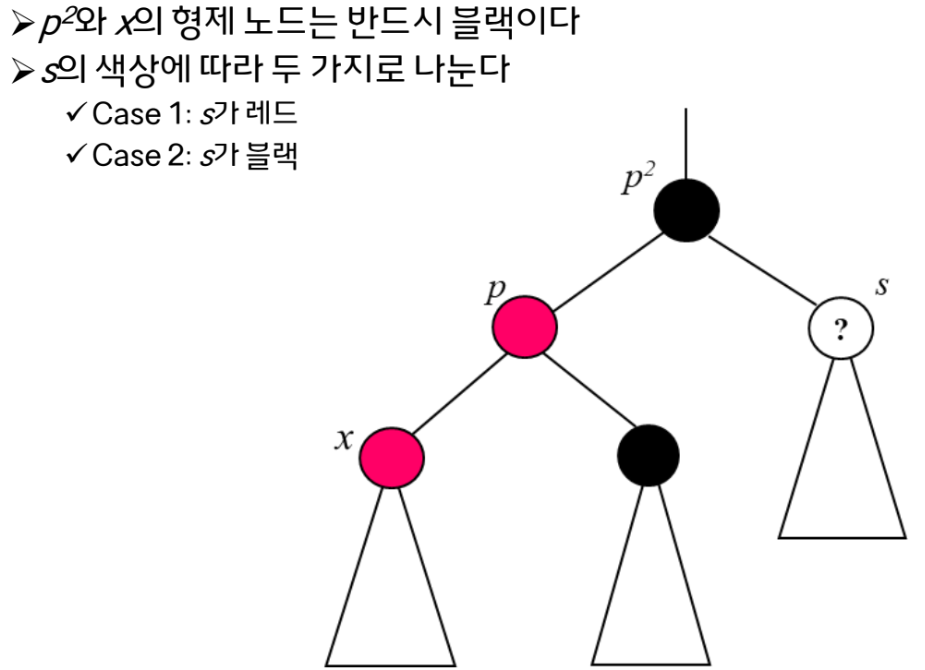
- 삼촌 노드 black: restructing
- 삼촌 노드 red: recoloring

삼촌 노드($s$)가 Red

• 부모노드($p$)와 삼촌 노드($s$)를 black으로 바꾼다.
• 이후 조부모 노드($p^2$)를 red로 변경한다.

다만 이거는 subtree여서 (10이 root가 아님) 끝나지만 만약 10의 ($p^2$)의 부모 노드가 red라면 또 부모-자식 노드가 red인 상황이 발생하니 재귀적으로 다시 판단하여 수정을 진행해야한다.
(그때 case에 맞게 recoloring 또는 restructing)

삼촌 노드($s$)가 Black

삼촌이 black이고 삽입하려는 노드가 왼쪽 자식인지 오른쪽 자식인지에 따라 case가 2개로 나뉜다.

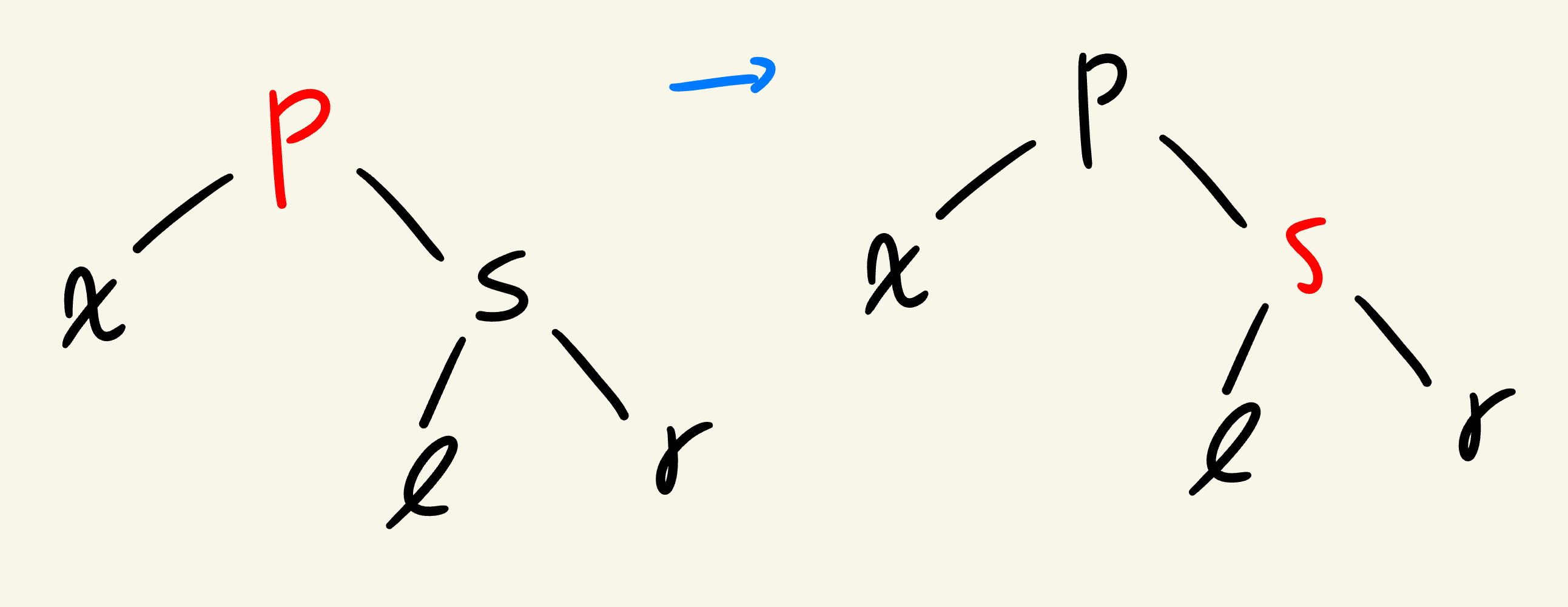
case1) s가 black이고 x가 p의 오른쪽 자식 (LR Case)

case2로 만들어주는 rotate를 통해 case2를 만들고 해결하면 된다.

case2) s가 black이고 x가 p의 왼쪽 자식 (LL case)

$p^2$를 기준으로 오른쪽으로 회전하면 $p$가 올라오고 $p^2$는 $p$의 오른쪽 자식으로 내려간다.

$y$의 이동: $p$의 원래 오른쪽 자식이던 $y$는 갈 곳을 잃지만,
BST 속성$(p < y < p^2)$을 만족시키기 위해 $p^2$의 새로운 왼쪽 자식이 된다.

색상 변경: 마지막으로, 규칙에 따라 새로운 루트가 된 $p$는 Black으로, 아래로 내려간 $p^2$는 Red로 색상을 바꿔주어 균형을 맞춥니다.

삭제

• 삭제노드가 레드라면 아무 문제 없음
• 삭제노드가 블랙이어도 유일한 자식이 레드이면 문제 없음 (recoloring 하면 됨)

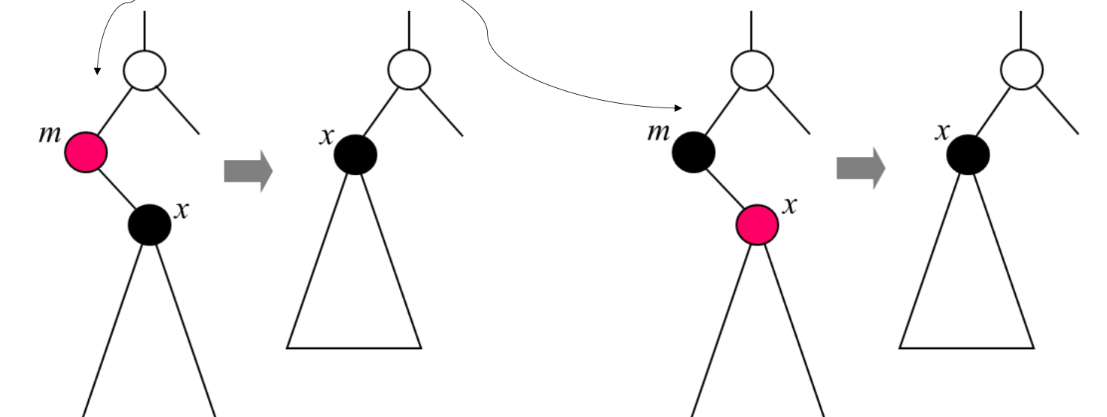
하지만 빨강 노드의 자식 노드는 검정색이다. (빨강 부모, 빨강 자식 불가) 이 특성이 깨지면 복잡해진다.

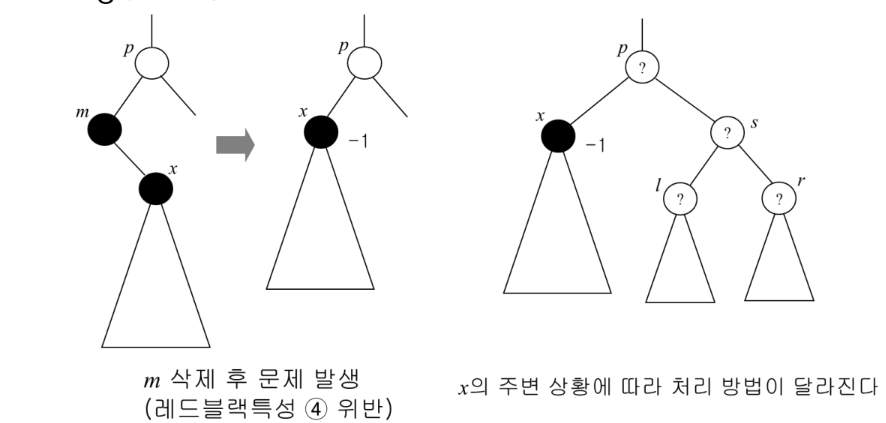
이럴 경우 총 5가지 경우로 case를 나누어 처리한다.

case1) p가 레드 (s는 반드시 블랙). <l의 색상, r의 색상>에 따라

Case 1-1 <블랙 블랙>

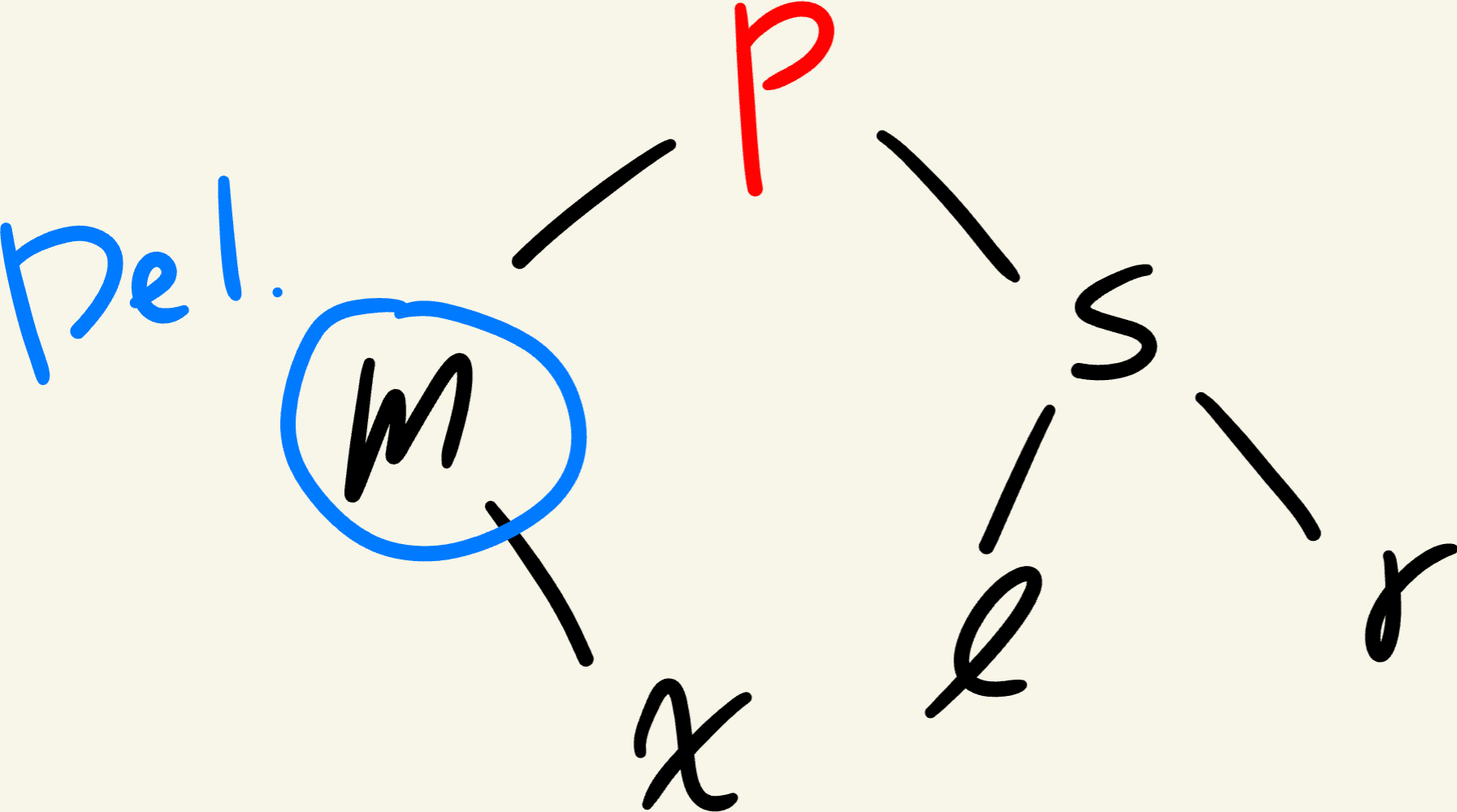
위와 같은 RB-Tree에서 $m$을 삭제하면 $p$에서 왼쪽으로 NIL 노드를 만나러 갈때 만나는 black은 1개이지만,
오른쪽으로 NIL 노드를 만나러 갈때 만나는 black은 2개이므로 불균형이 발생한다.

이 경우 $p$와 $s$의 색상을 바꿈으로 해결할 수 있다.

• x에 이르는 경로상 블랙이 추가되므로 루트에서 s를 지나는 경로상 블랙 노드 수 변화 없음

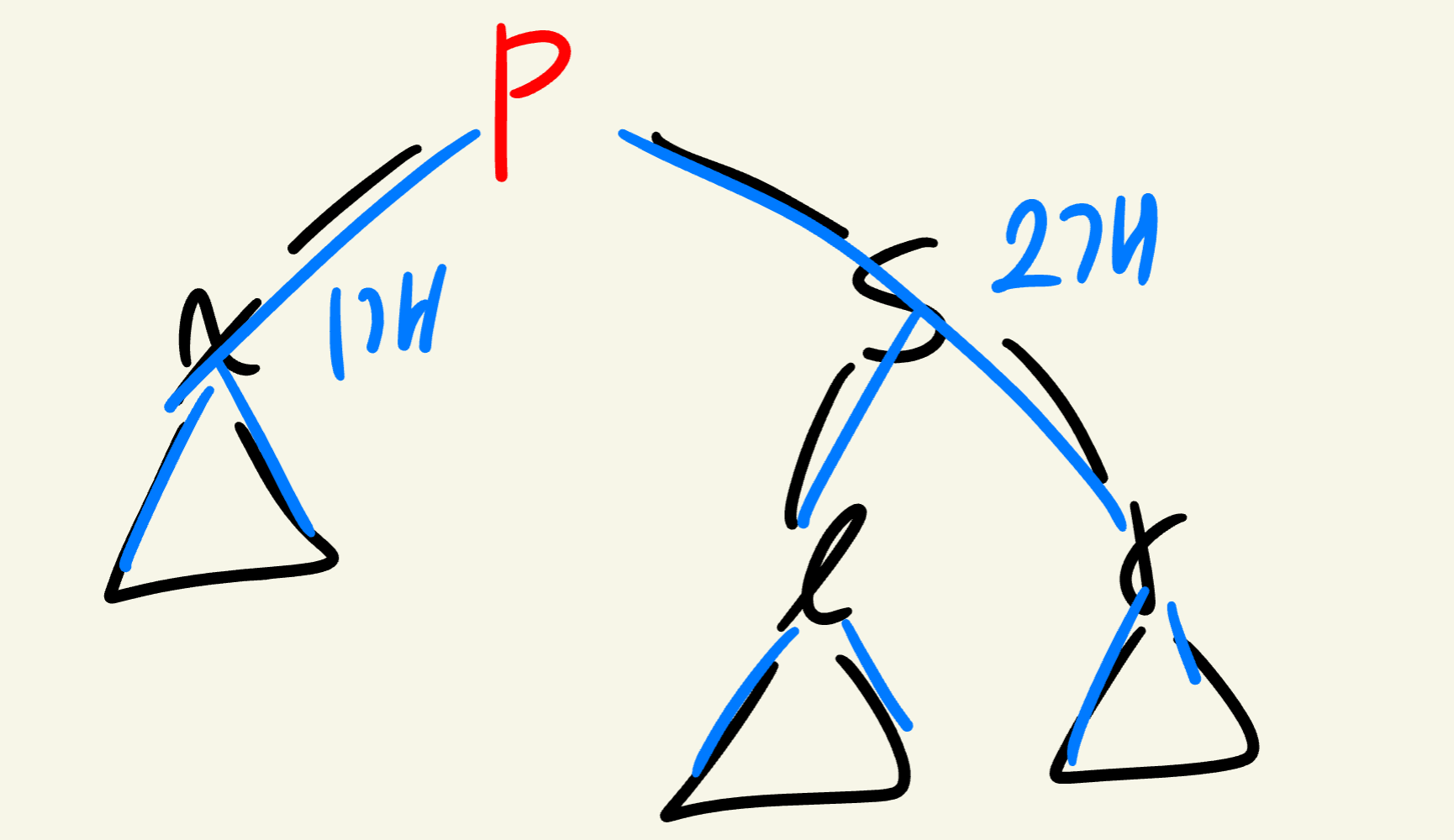
Case *-2

$m$이 삭제되면 그 경로의 Black-Height가 1 부족해진다.
($x$가 double-black 상태).

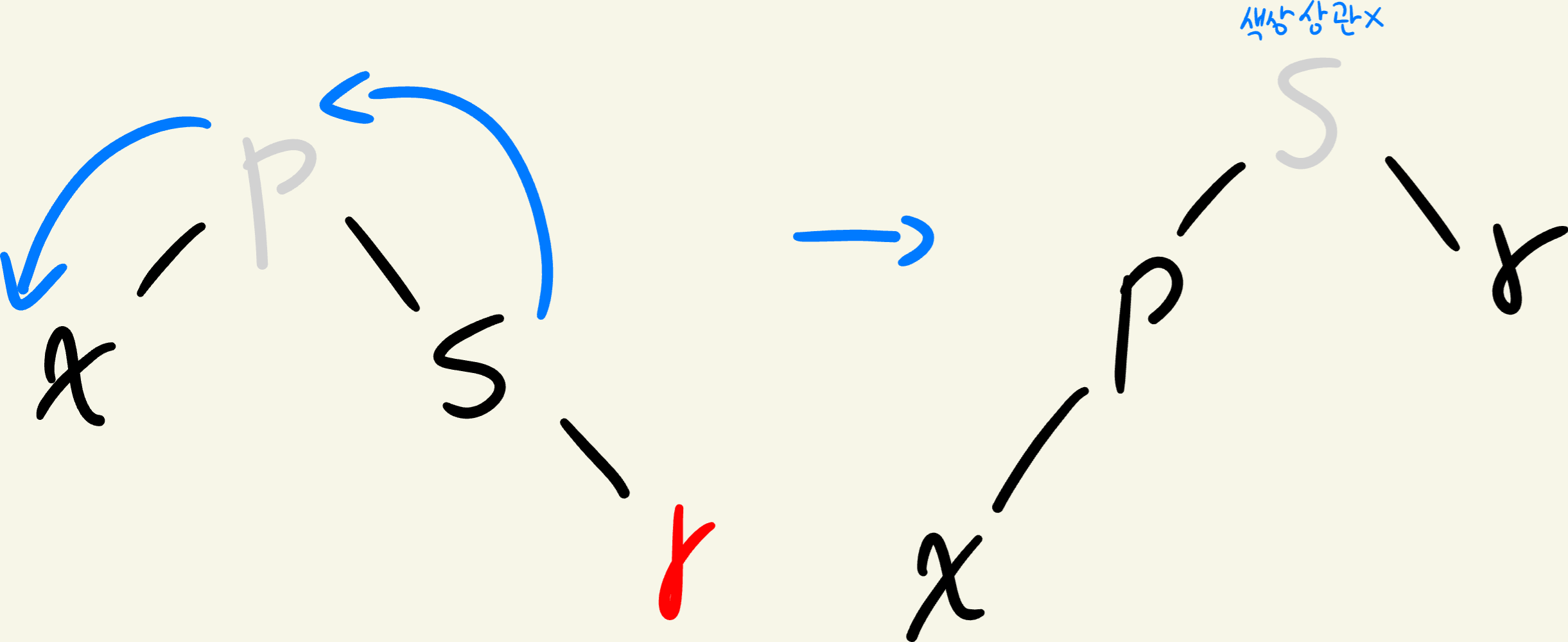
1. p를 중심으로 왼쪽으로 회전
2. p와 s의 색상을 바꿈
3. r의 색상을 레드에서 블랙으로 바꿈으로 해결할 수 있다.

$x$에 이르는 경로상 블랙이 추가되므로 루트에서 $s$를 지나는 경로상 블랙 노드 수 변화 없음

Case *-3

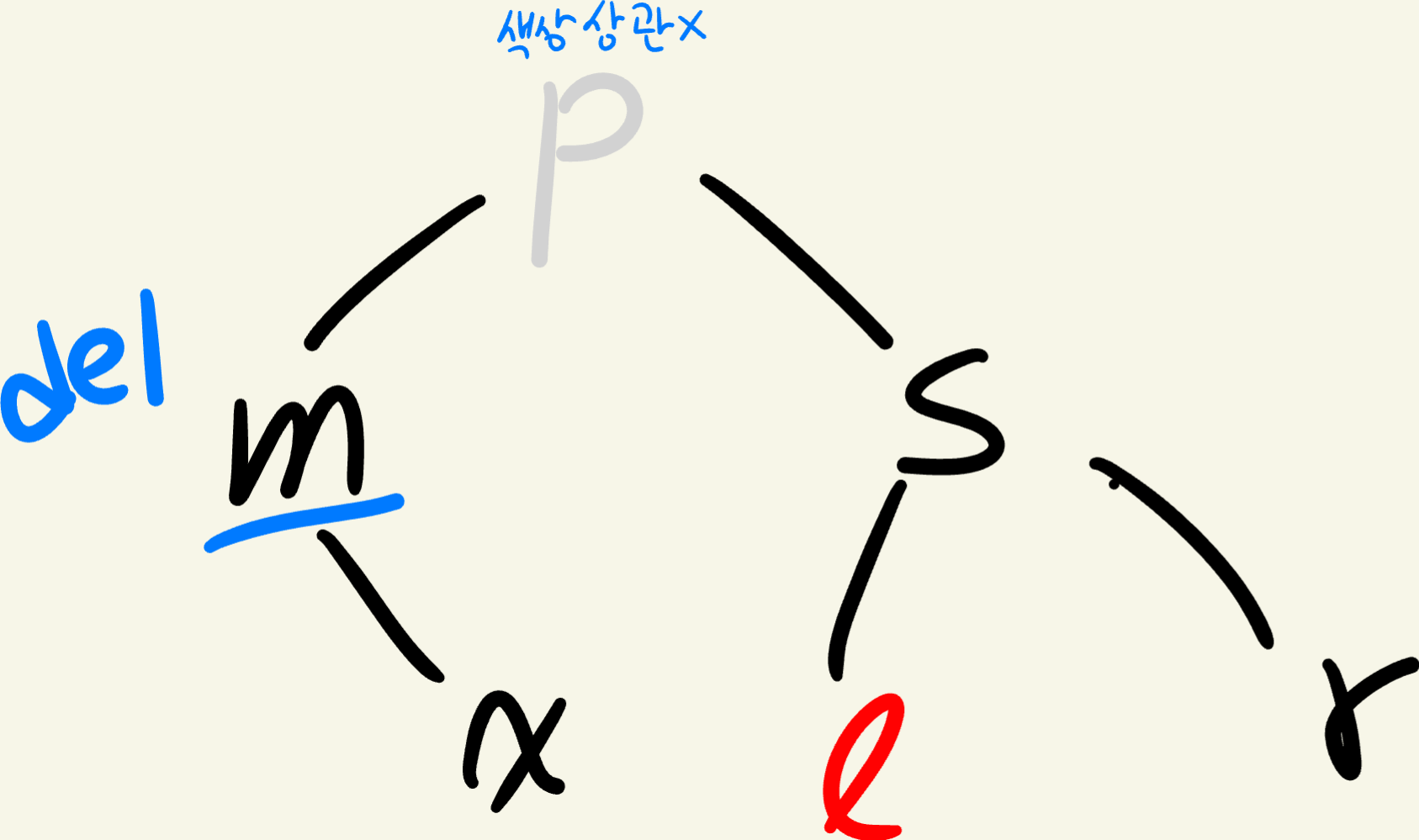
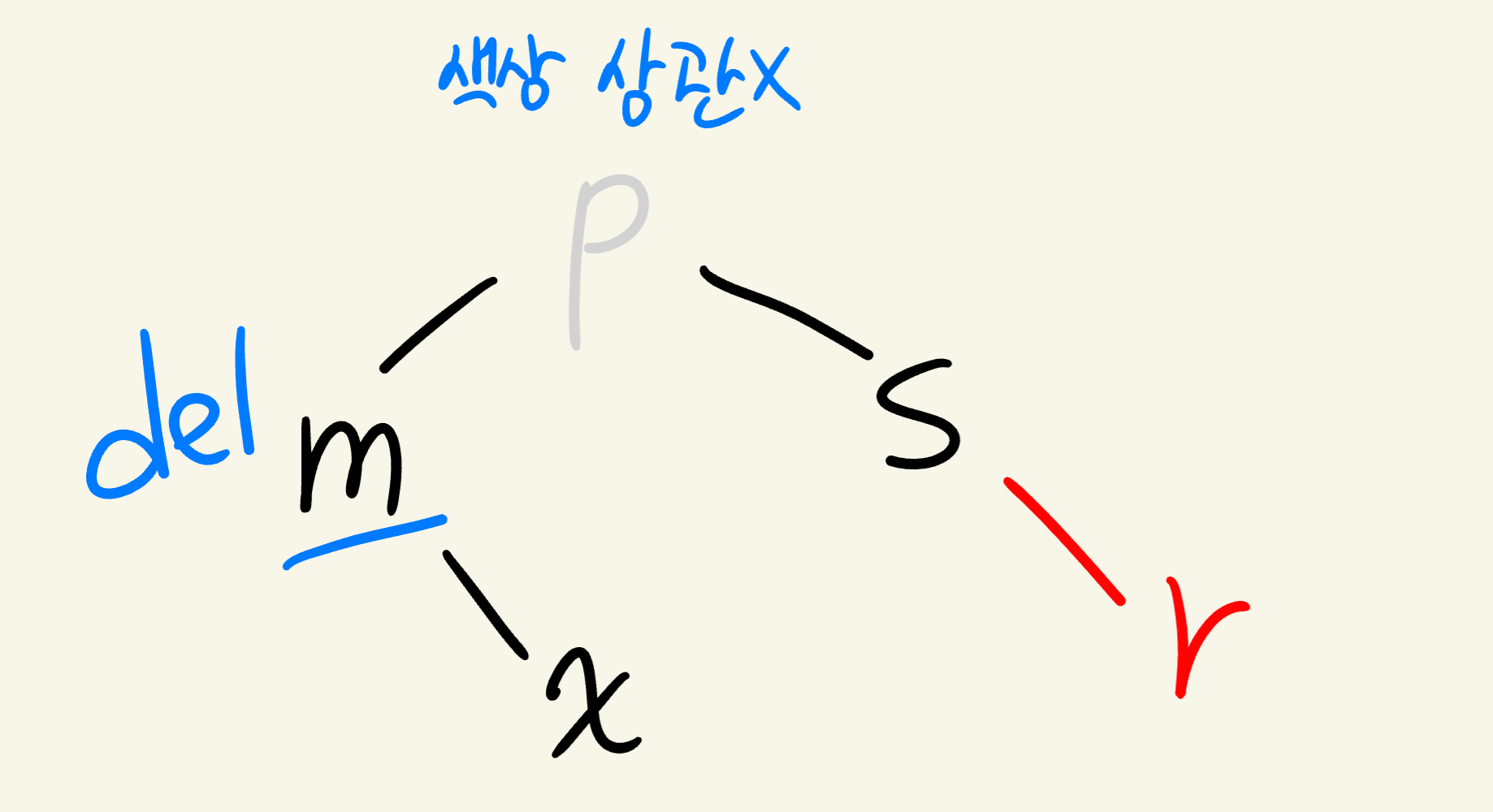
위 case에서 m을 삭제하게되면 형제(s)는 Black입니다.

가까운 조카(l)는 Red입니다.

먼 조카(r)는 Black입니다.

이 상황에서는 Red 노드인 l을 먼 쪽으로 보내주어 최종적으로 해결할 수 있는 Case *-2 형태로 바꿔주는 것이 목표입니다.

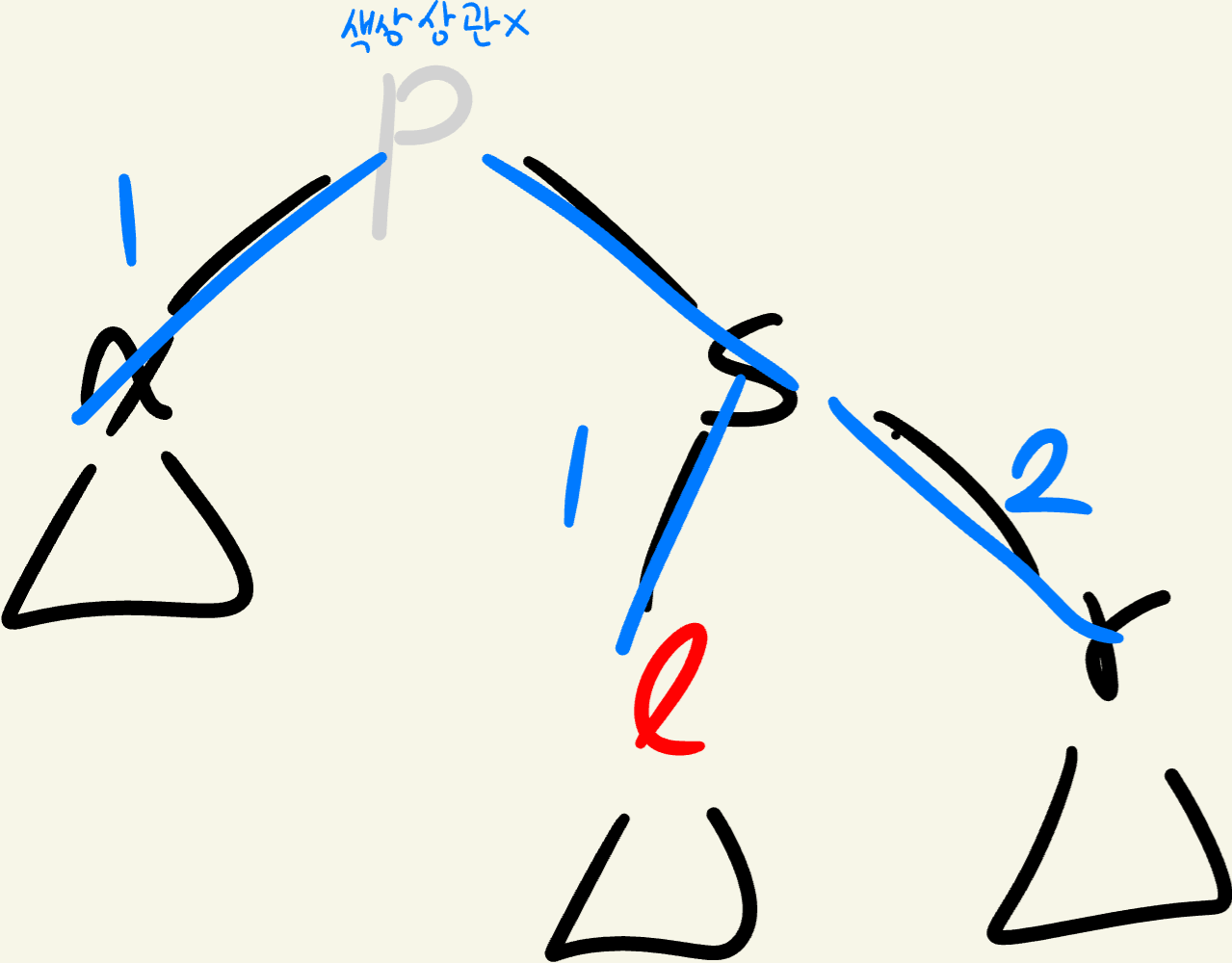
1단계: s를 중심으로 오른쪽으로 rotate를 진행한다.
s를 축으로 오른쪽 회전을 하면 l이 s의 자리로 올라오고, s는 l의 오른쪽 자식이 된다.

2단계: l과 s의 색상 교환: rotate 후, 새로운 형제가 된 l을 Black으로, 그 자식이 된 s를 Red로 교체

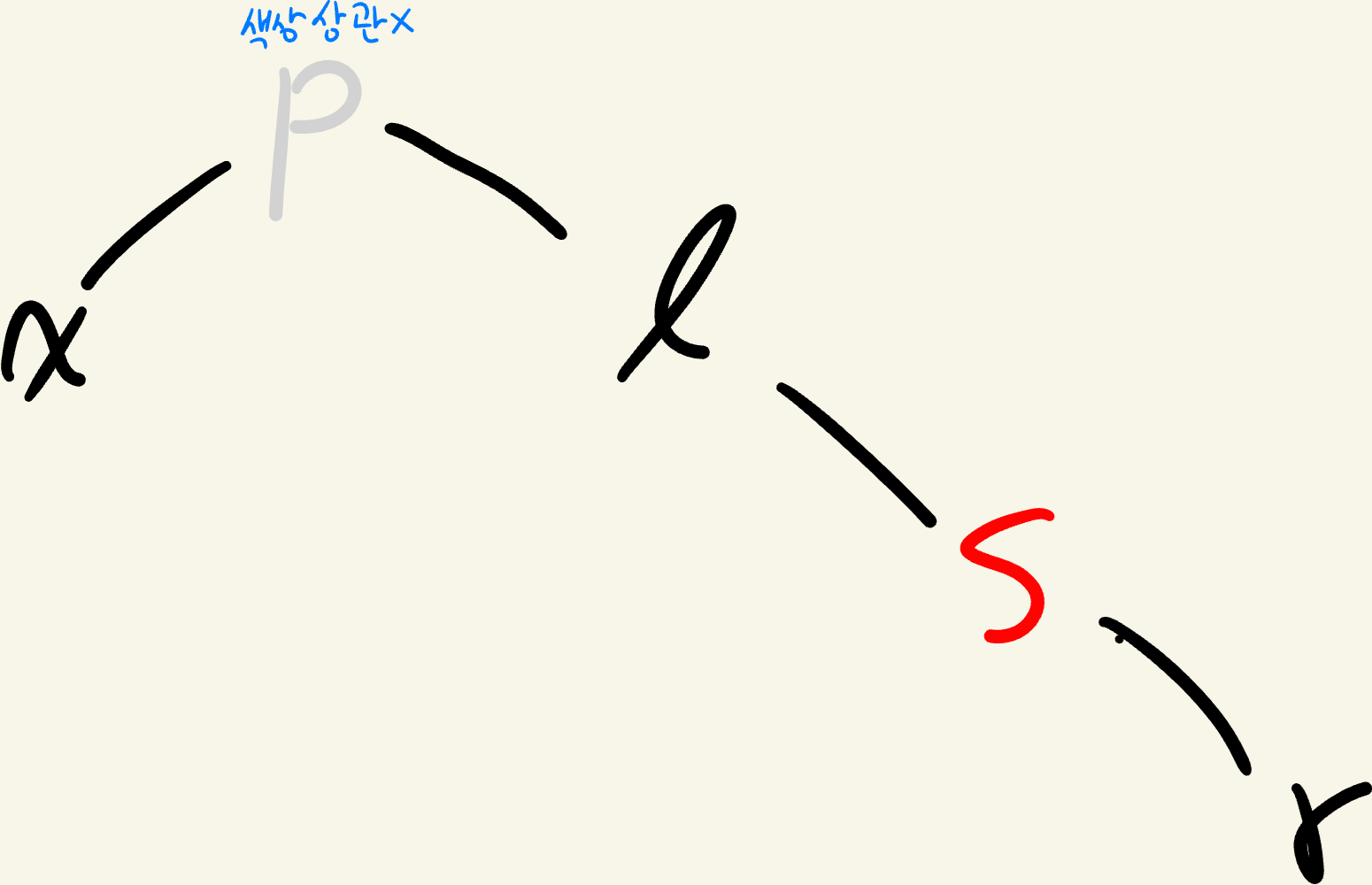
이렇게 되면 case *-2 처리를 해주면 된다.

Case 2) p가 블랙 <s의색상, l의색상, r의 색상>에 따라

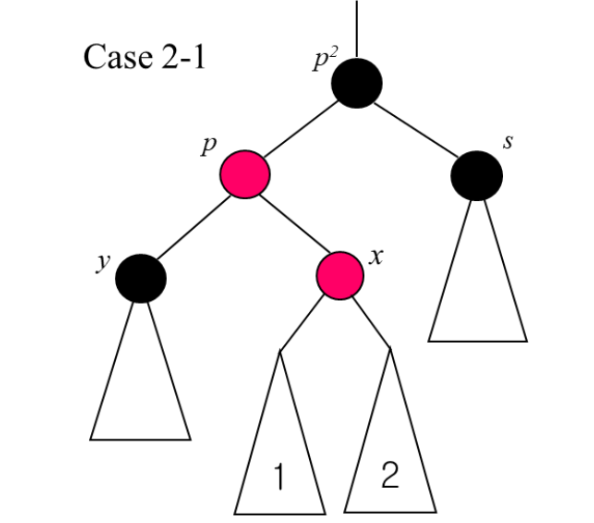
Case 2-1) <블랙 블랙 블랙>

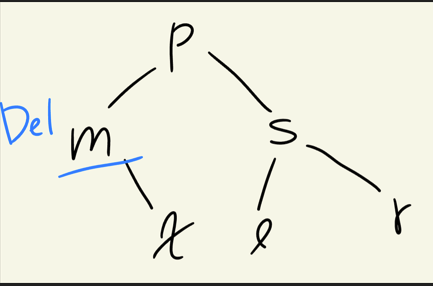
위와 같이 m을 삭제하면

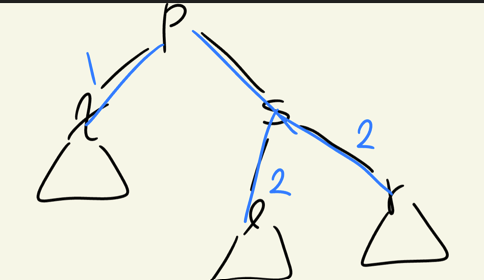
삭제된 노드(m)가 Black이어서, 그 자리를 대체한 x 경로에 Black-Height가 1 부족한 'Double Black' 문제가 발생한다.

이 문제를 해결하기 위해 주변을 살펴보면, x의 형제 노드 s가 Black, s의 두 자식 l과 r도 모두 Black이다.

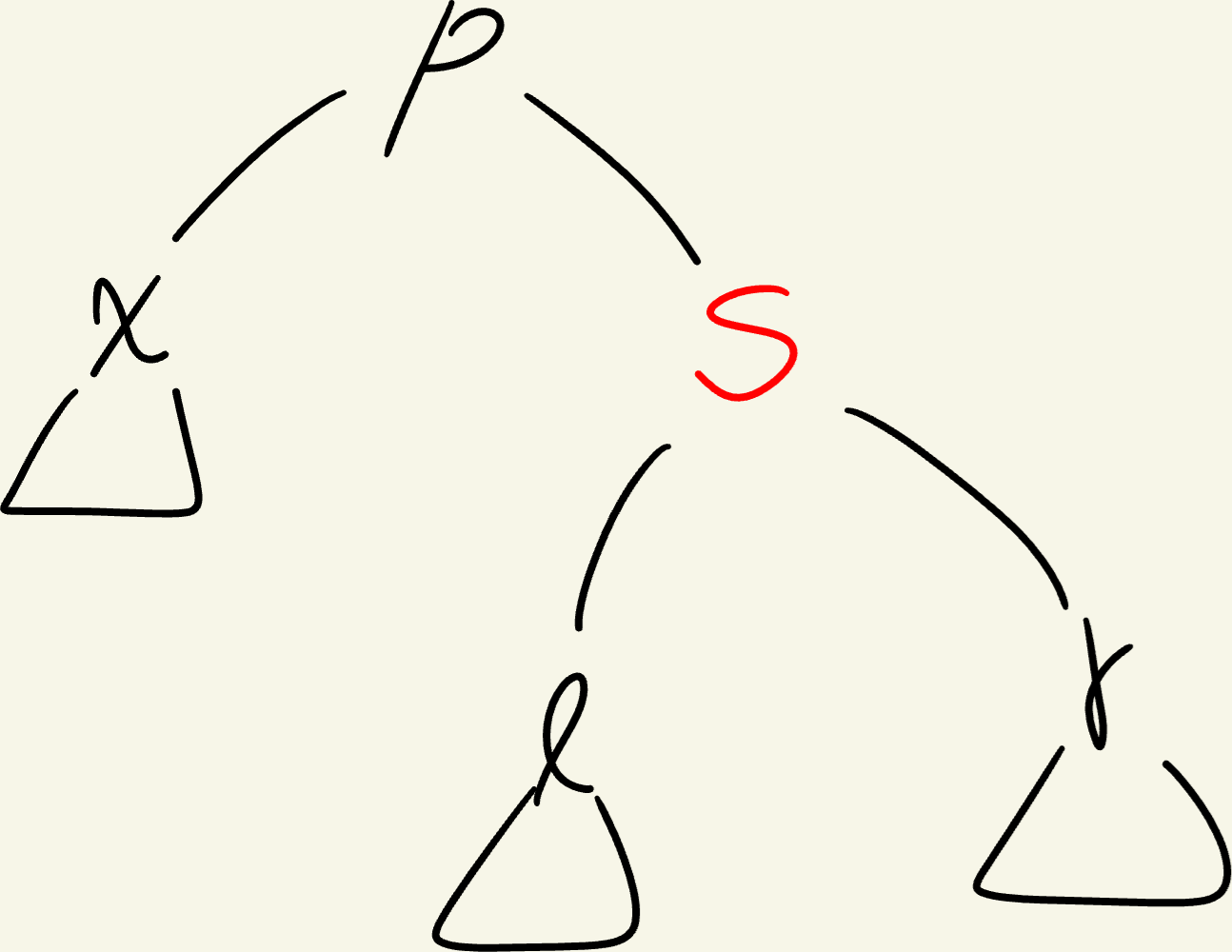
이렇게 s를 red로 바꿔주면 되지만 다시 p를 확인하고 문제가 발생하는지 체크해야한다.

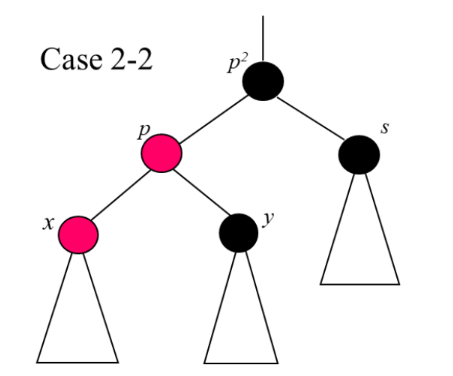
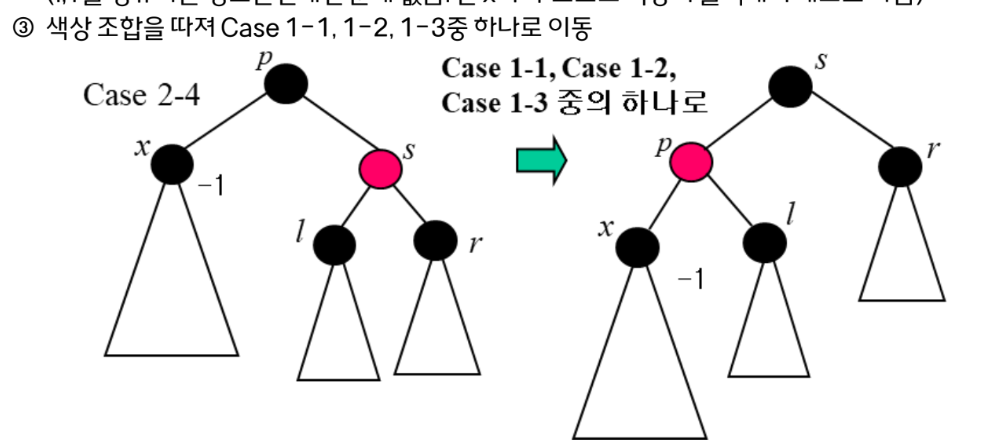
2-4)

얜 그냥 삭제만 하면 되는데

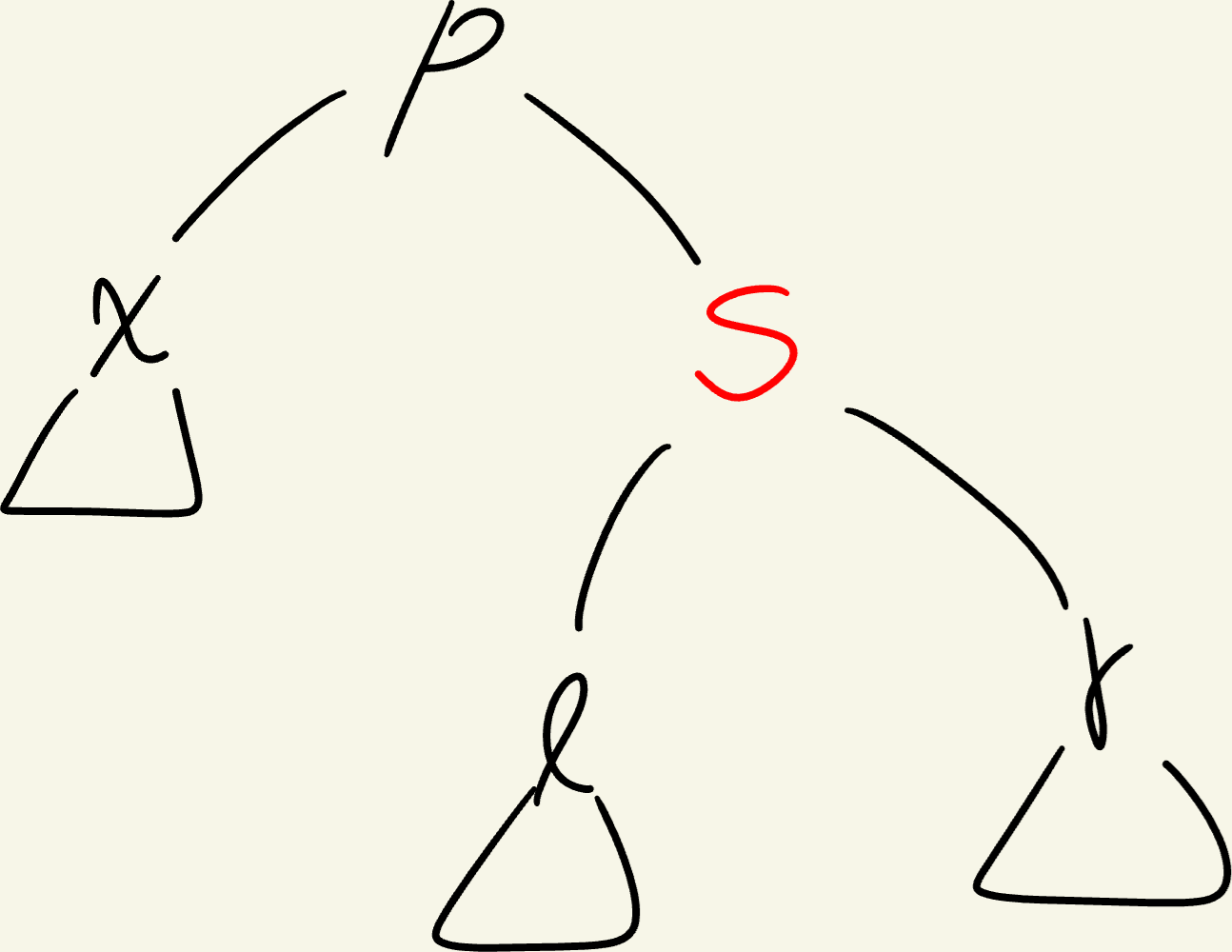
이러면 색상 조합을 따져서 rotate를 해주면 된다.

Red-Black Tree작업 성능

키가 총 n개인 레드블랙트리의 가능한 최대 깊이는 $O(logn)$이다.

• 키가 n개라면 내부노드의 수가 n개
• 트리의 깊이는 $log n +1$
• 루트에서 임의의 리프에 이르는 경로의 블랙노드는 아무리 잘 만들어져도 $log n +1$을 넘을 수 없음
• 레드노드는 두개 연속해서 존재할 수 없으므로 블랙노드보다 적음
• 임의의 리프에 이르는 총 길이는 $2( log n +1)$을 넘을 수 없음

출처

Algorithm [#5-1 Search Tree], Chungbuk National University, School of Computer Science, Prof. Lee, Euijong, 2025 FALL .pdf (교수님 수업자료)

https://www.geeksforgeeks.org/dsa/introduction-to-red-black-tree/

https://seokyoungg.tistory.com/101#1.%20%ED%8A%B9%EC%A7%95%C2%A0

https://www.youtube.com/watch?v=qvZGUFHWChY&list=PL9xmBV_5YoZNqDI8qfOZgzbqahCUmUEin