B tree

Tae_Tae·2025년 11월 22일

자료구조 / 알고리즘 (C)

목록 보기

27/29

이진탐색트리(BST)를 일반화한 트리로 B-tree는 다진검색트리가 균형을 유지함으로 최악의 경우 디스크 접근 횟수를 줄이고자 하는 트리의 형태이다.

특징

부모 노드는 자식 노드를 2개 이상 가질 수 있다.
루트를 제외한 모든 노드는 x개의 키를 갖는다.
노드가 자녀를 x개 가졌다면, key는 x-1개를 가진다.
노드 내의 key는 오름차순으로 저장된다.
모든 리프 노드는 같은 깊이를 갖는다.

M을 기준으로

M: 각 노드의 최대 자녀 노드 수
M-1: 각 노드의 최대 key 수
⌈ M/2 ⌉: 각 노드의 최대 자녀 노드 수 (root node, leaf node 제외)
⌈ M/2 ⌉-1: 각 노드의 최대 key 수 (root node 제외)

삽입

추가는 leaf에 이루어지고, root를 타고 적절한 leaf 노드에 도달하면 삽입이 진행된다.
오버플로우 발생 시 가운데 노드를 승격시키고 좌우 노드를 분할하여 준다.

BTreeInsert(t, x) {
	x를 삽입할 리프 노드 r을 찾는다;
	x를 r에 삽입한다;
	if (r에 오버플로우 발생)
    	then clearOverflow(r);
}

clearOverflow(r) {
	if (r의 형제 노드 중 여유가 있는 노드가 있음)
    	then {r의 남는 키를 넘긴다};
    else {
    r을 둘로 분할하고 가운데 키를 부모 노드로 넘긴다;
    	if (부모 노드 p에 오버플로우 발생)
        	then clearOverflow(p);
    }
}

예시

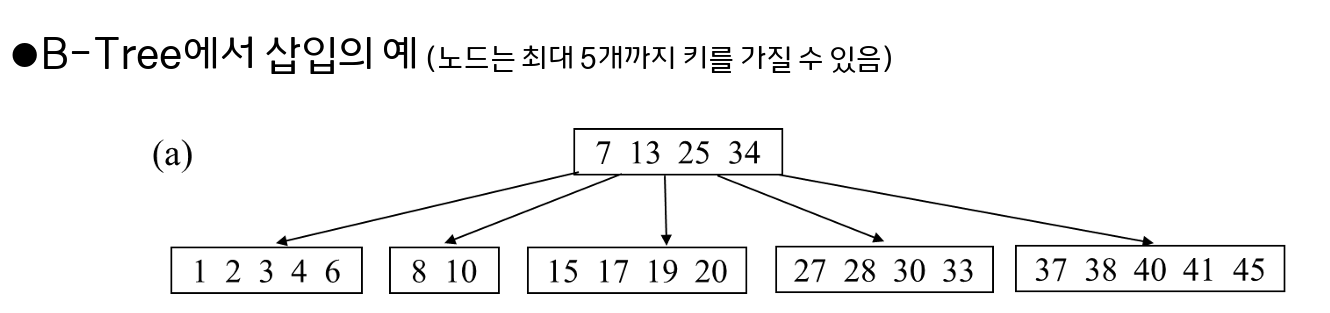
위와 같은 b tree가 있다고 하고 여기에 9, 31이 삽입된다고 하면

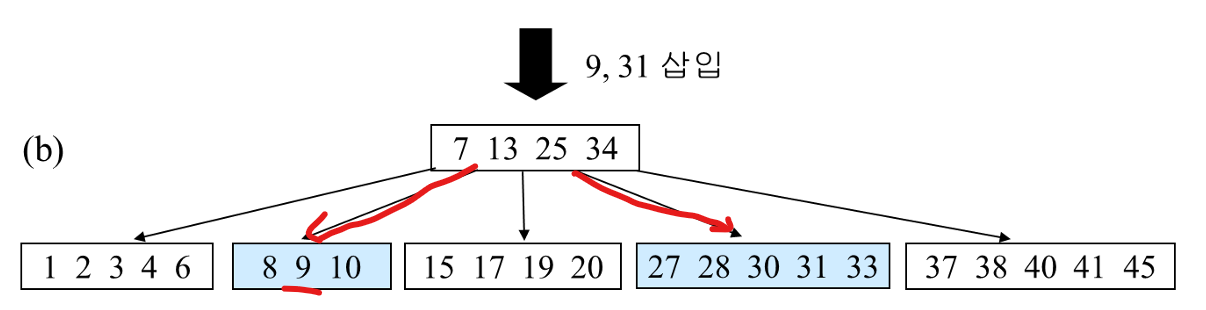
9는 7 < 9 < 13 사이에 있는 값으로 해당 리프 노드로 보내고,
31은 25 < 31 < 35로 해당 리프 노드로 보내서 삽입을 한다.
이 경우 오버플로우가 발생하지 않았으니 삽입 종료

하지만 여기에 5를 추가로 삽입한다면 오버플로우가 발생한다.

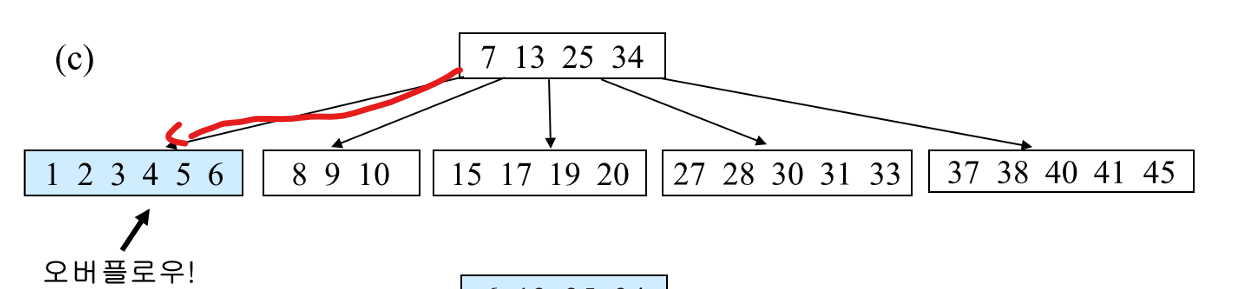
그러면 형제 노드 중 바로 옆 노드(8, 9, 10)가 여유 공간이 있으므로 여기에 오버플로우 된 키를 넘긴다.

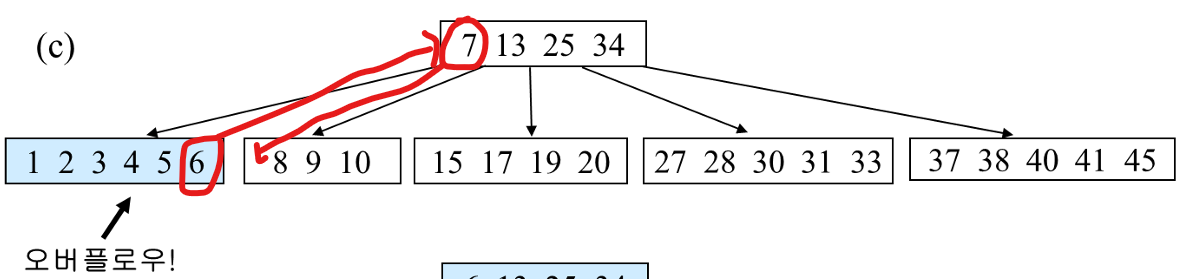
6을 그대로 8 9 10이 있는 곳에 넘기면 부모노드의 key값에 따른 조건에 맞지 않으므로 위와 같은 과정을 거쳐서 키를 넘기면
오버플로우가 해결된다.

또 여기에 39를 삽입하게 된다면 오버플로우가 발생한다.

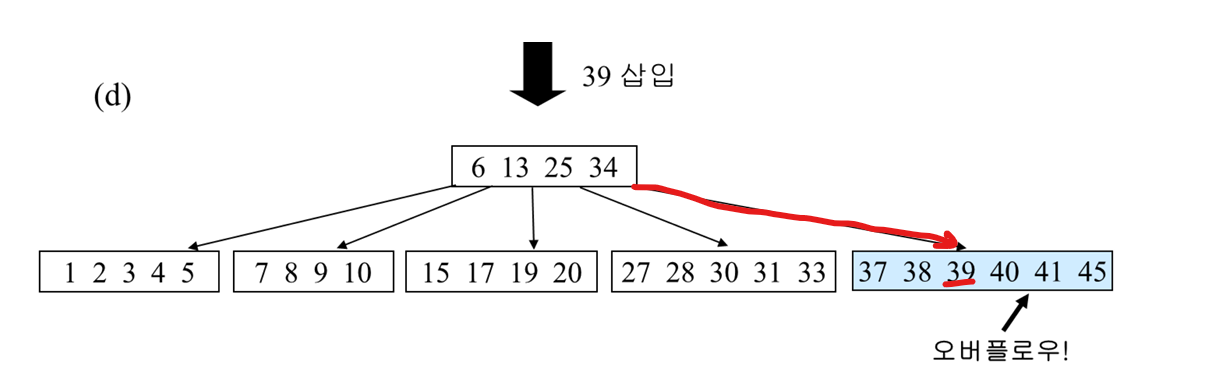
형제 노드 중 여유 공간이 있는 노드가 없으니, 가운데 노드를 승격 시키고 분할을 해야한다.

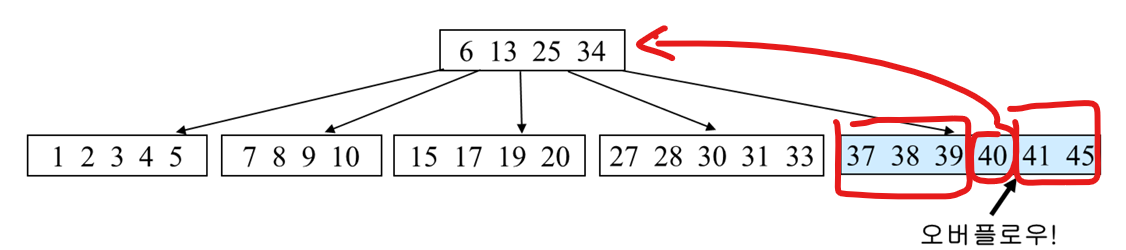
그러면 아래와 같이 오버플로우가 해결된다.

여기서 더 삽입을 진행보자

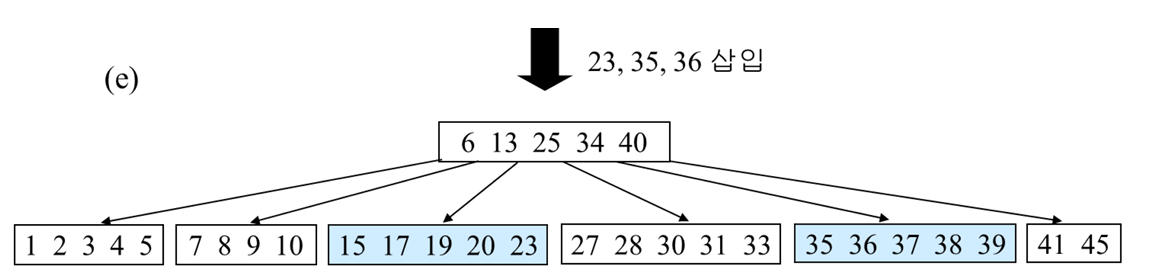
위 b tree에 32를 삽입하게 되면

오버플로우가 발생하고 형제 노드 중 여유가 있는 노드가 없으므로 분할하고 승격해서 오버플로우를 해결해야한다.

그런데 이러면 부모노드에서 또 오버플로우가 발생한다.
그러면 재귀적으로 부모노드에서도 오버플로우 해결을 해줘야한다.

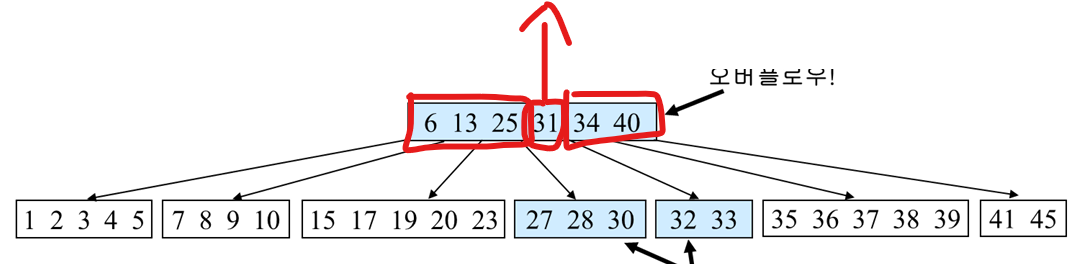
기존 부모 노드는 형제 노드가 없으므로 바로 분할하고 승격해서 해결한다.

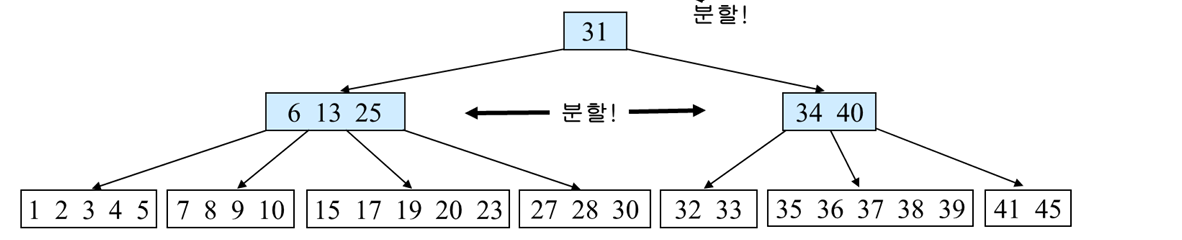
그러면 위와같이 오버플로우가 해결 된 모습을 볼 수 있다.

삭제

삭제는 항상 leaf node에서 진행된다.

x를 키로 갖고 있는 노드를 찾음
이 노드가 리프노드가 아니라면 x의 직후원소 y를 가진 리프노드 r을 찾아 x, y를 맞바꿈
리프노드에서 x를 제거
x제거 후 노드에 언더플로우가 발생하면 이를 해소

// t : 트리의 루트 노드
// x : 삭제하고자 하는 키
// v : x를 갖고 있는 노드

BTreeDelete(t, x, v) {
	if (v가 리프 노드 아님)
    	then {
        x의 직후원소  y를 가진 리프 노드를 찾는다;
        x와  y를 맞바꾼다;
        }
    리프 노드에서 x를 제거하고 이 리프 노드를  r이라 한다;
    
    if (r에서 언더플로우 발생)
    	then clearUnderflow(r);
}
clearUnderflow(r) {
	if ( r의 형제 노드 중 키를 하나 내놓을 수 있는 여분을 가진 노드가 있음)
    	then {
        	r이 키를 넘겨받는다;
        }
   else {
   	r의 형제 노드와 r을 합병한다;
   		if (부모 노드 p에 언더플로우 발생)
    		then clearUnderflow(p);
   }
}

언더플로우가 발생하면 먼저 형제 노드에서 도움을 요청하고, 형제 노드에서도 도움을 못받으면, 합병 후 부모 노드에게서 도움을 받는다.
(부모 노드에서도 언더플로우 발생 시 재귀적으로 해결)

예시

아래의 b tree는 5차 b tree로 최소 key는 2개이다.
(5/2 올림 - 1 = 2)

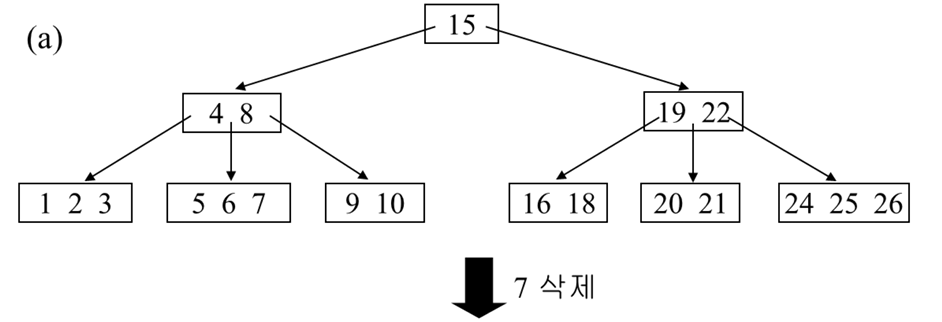
위 b tree에서 7을 삭제한다면 리프노드니까 그냥 삭제하면 된다.

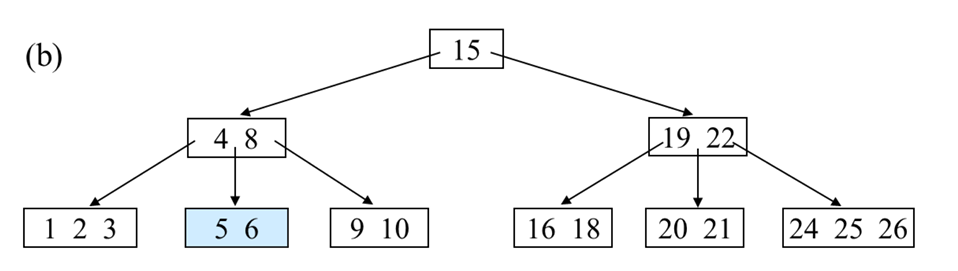
하지만 여기서 4를 삭제한다면, internal node이므로 위치를 바꾸고 삭제해야한다.
internal node 삭제의 경우 prodecessor(나보다 작은 데이터들 중 가장 큰 데이터) 혹은 successor(나보다 큰 데이터들 중 가장 작은 데이터)와 교체한 후 leaf 노드로 보내어 삭제를 진행한다.

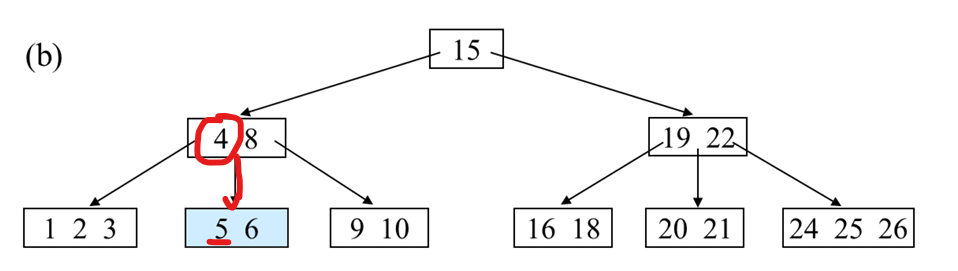
4보다 큰 데이터 중 가장 작은 값인 5와 교환을 하고 삭제를 한다.

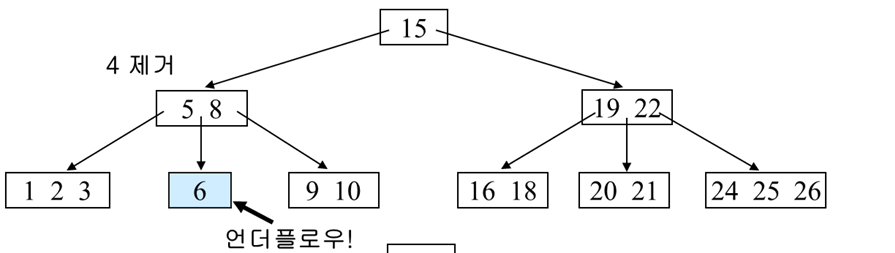
근데 그러면 언더플로우가 발생하므로, 형제 노드에서 먼저 도움을 요청해본다.

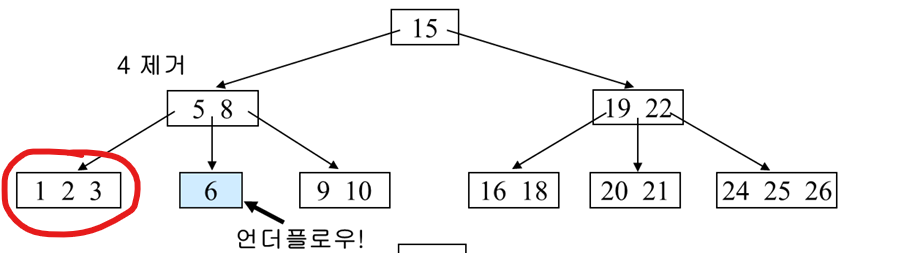
왼쪽 -> 오른쪽 -> 부모 순서로 도움을 요청하니 왼쪽 먼저 체크했는데, 왼쪽이 여유가 있다.

그럼 왼쪽에서 하나를 도움 받으면 된다.

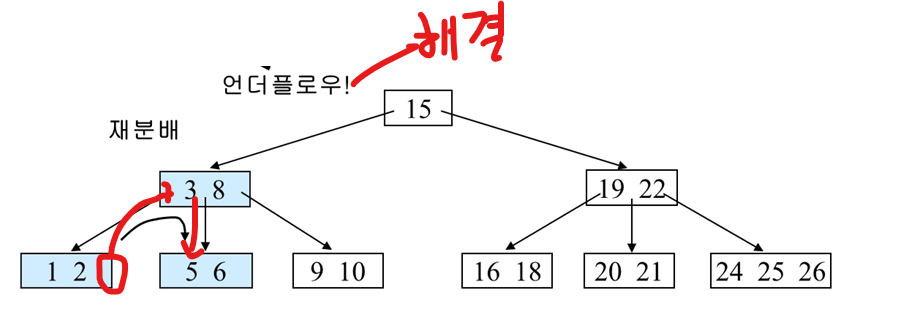
바로 3을 넣으면 규칙에 위배되니, 부모노드로 올리고 도움을 받는 식으로 규칙을 지키며 언더플로우를 해결한다.

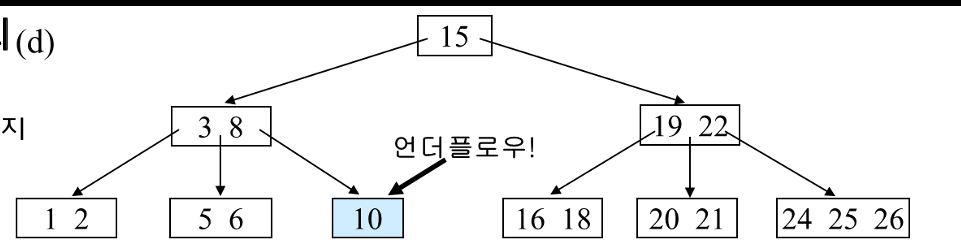
여기서 또 9를 삭제한다면, 언더플로우가 발생한다.

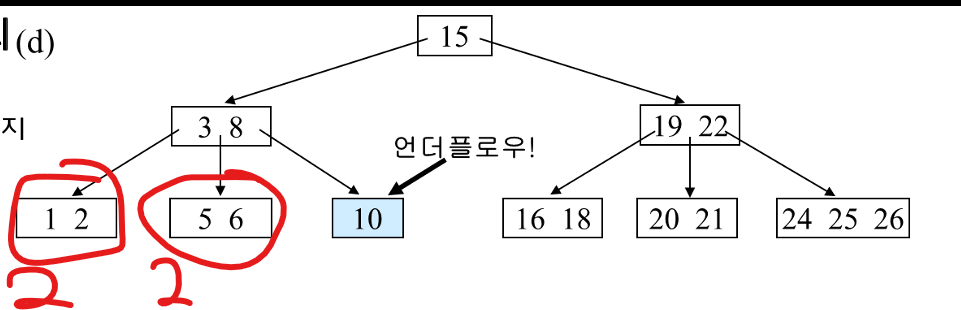
형제 노드들도 key가 2개 뿐이라 도움을 받을 수 없다.
부모 노드에게 도움을 받자

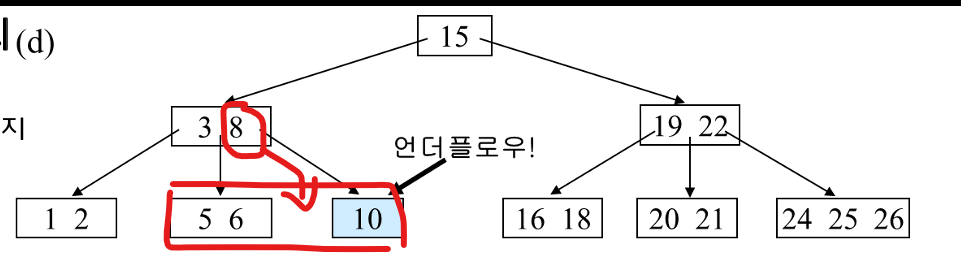
왼쪽 형제와 병합 후 부모에게 도움을 받아서 언더플로우를 해결한다.

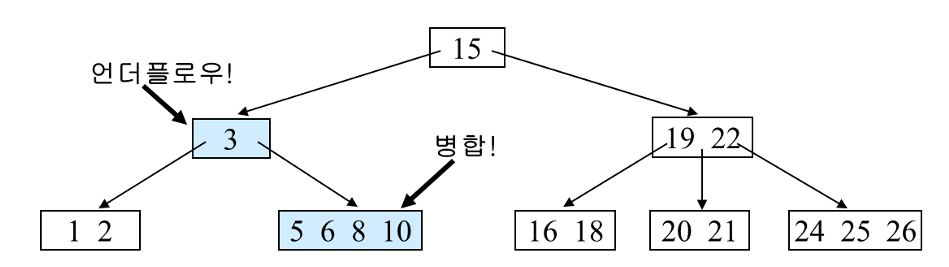
이러면 부모노드에서 언더플로우가 발생하는데, 재귀적으로 해결하면 된다.

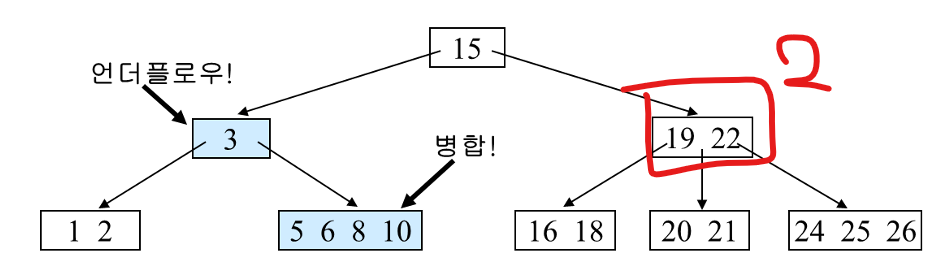
부모 노드의 형제 노드도 key가 여유가 없으니, 다시 병합 후 부모노드에게 도움을 받아야한다.

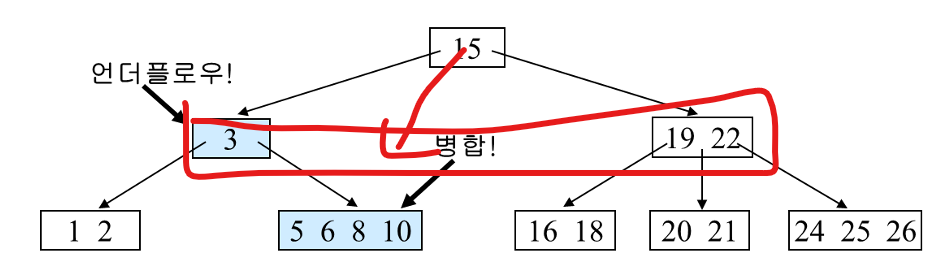
그래서 위와 같이 병합을 하면 루트 노드가 비는데 이거는 그냥 삭제하면 된다.

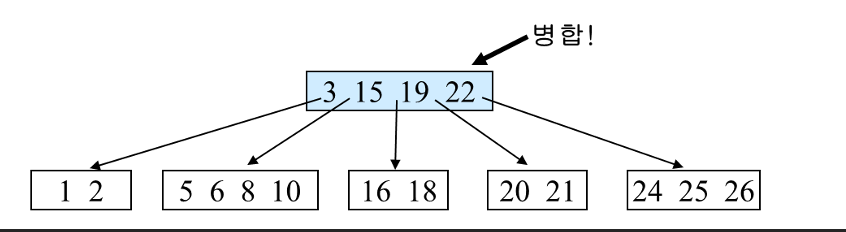
언더플로우 해결 끝

작업 성능 분석

이진검색트리가 균형을 아주 잘 맞추면 높이가 $\log_2n$ 에 근접
m진검색트리가 균형을 아주 잘 맞추면 높이가 $\log_mn$ 에 근접
B-트리에서 임의의 노드가 최대 m개의 자식을 가질 수 있다면 루트를 제외하고 최소한 $\lfloor m/2 \rfloor$ 개의 자식을 가져야 함
- B-트리의 깊이는 최악의 경우에도 대략 $\log_{\left\lfloor \frac{m}{2} \right\rfloor} n$ 보다 깊을 수 없으므로 $log_mn$ 과 $\log_{\left\lfloor \frac{m}{2} \right\rfloor} n$ 사이의 어떤 값이 됨

시간 복잡도

검색: O( $logn$ )
삽입: O( $logn$ )
삭제: O( $logn$ )

참고자료

https://www.youtube.com/watch?v=bqkcoSm_rCs
https://www.youtube.com/watch?v=H_u28u0usjA
Algorithm [#5-2 Search Tree(2)] 2025 FALL Chungbuk National University School of Computer Science Prof. Lee, Euijong

Tae_Tae

이전 포스트

Red Black Tree

다음 포스트