
정의
Union-find는 disjoint set들을 관리하기 위한 data structre로서, 아래 3개의 operation을 지원한다.
-
makeset(x): 단일 element x로 이루어진 set을 하나 생성한다.
-
find(x): x가 포함된 set을 return한다.
-
union(x, y): x가 포함된 set과 y가 포함된 set을 하나의 set으로 합친다.
예시
union
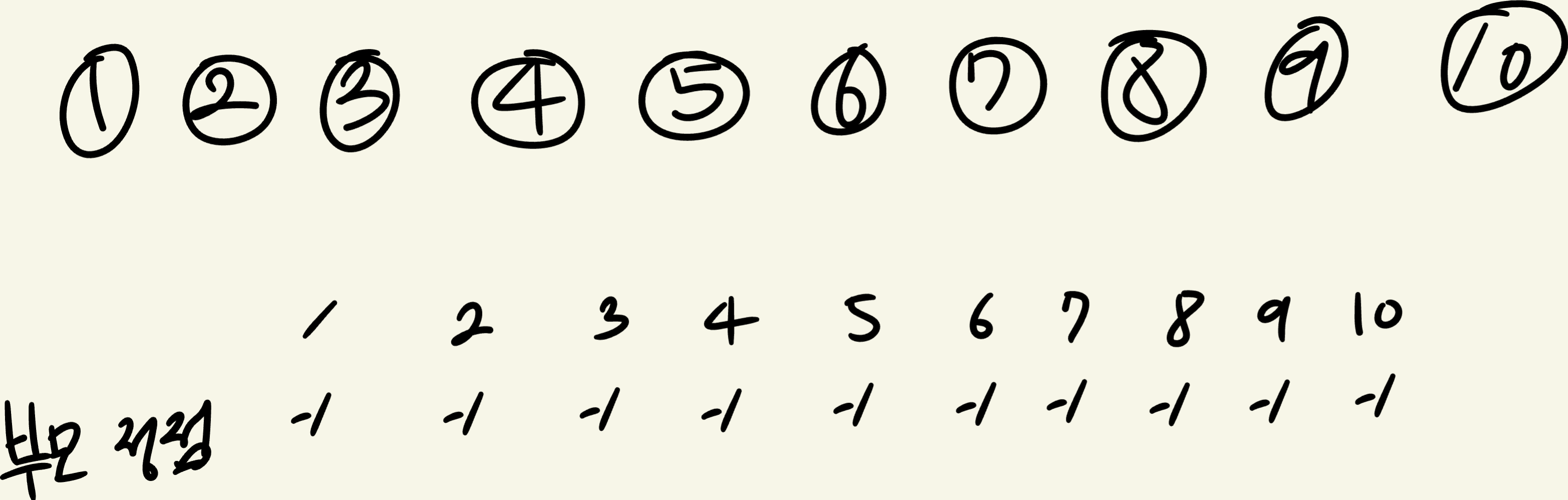
makeset으로 초기화를 진행해준다.
부모 정점이 없다는 뜻으로 -1을 채워준다.

Union(1, 5)를 진행하면 5을 1의 자식으로 만든다.

Union(2, 3) 또한 3을 2의 자식으로 만들면 된다.
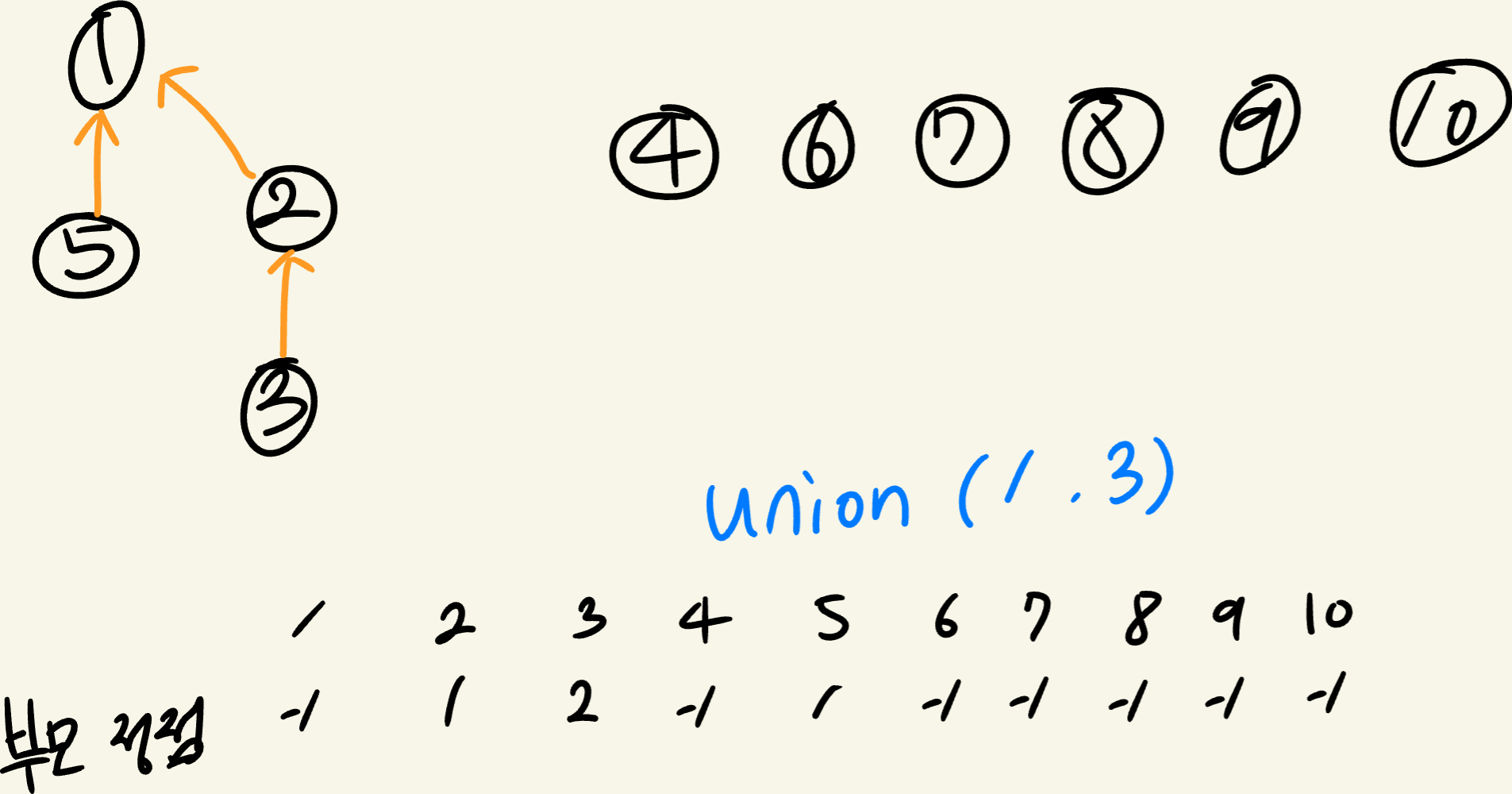
Union(1, 3) 을 하게되면 3을 1에 자식으로 Direct로 연결 하면 2가 버려지니, 2를 1의 자식으로 만들어 그룹이 합쳐지는 방식으로 Union을 한다.
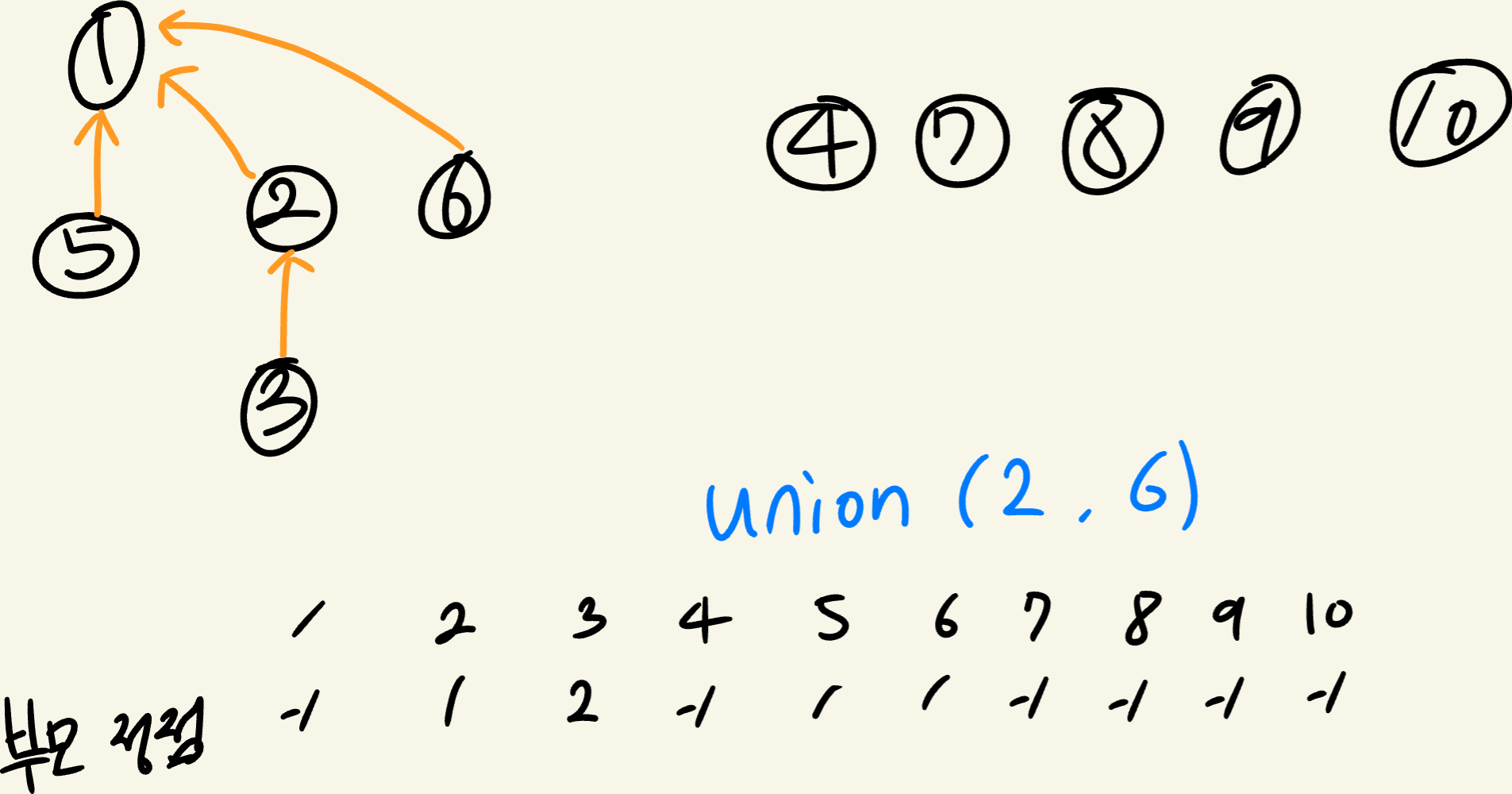
Union(2, 6) 을 진행하면 2에 연결하는 것이 아닌. 2의 부모에 6을 연결한다.
find
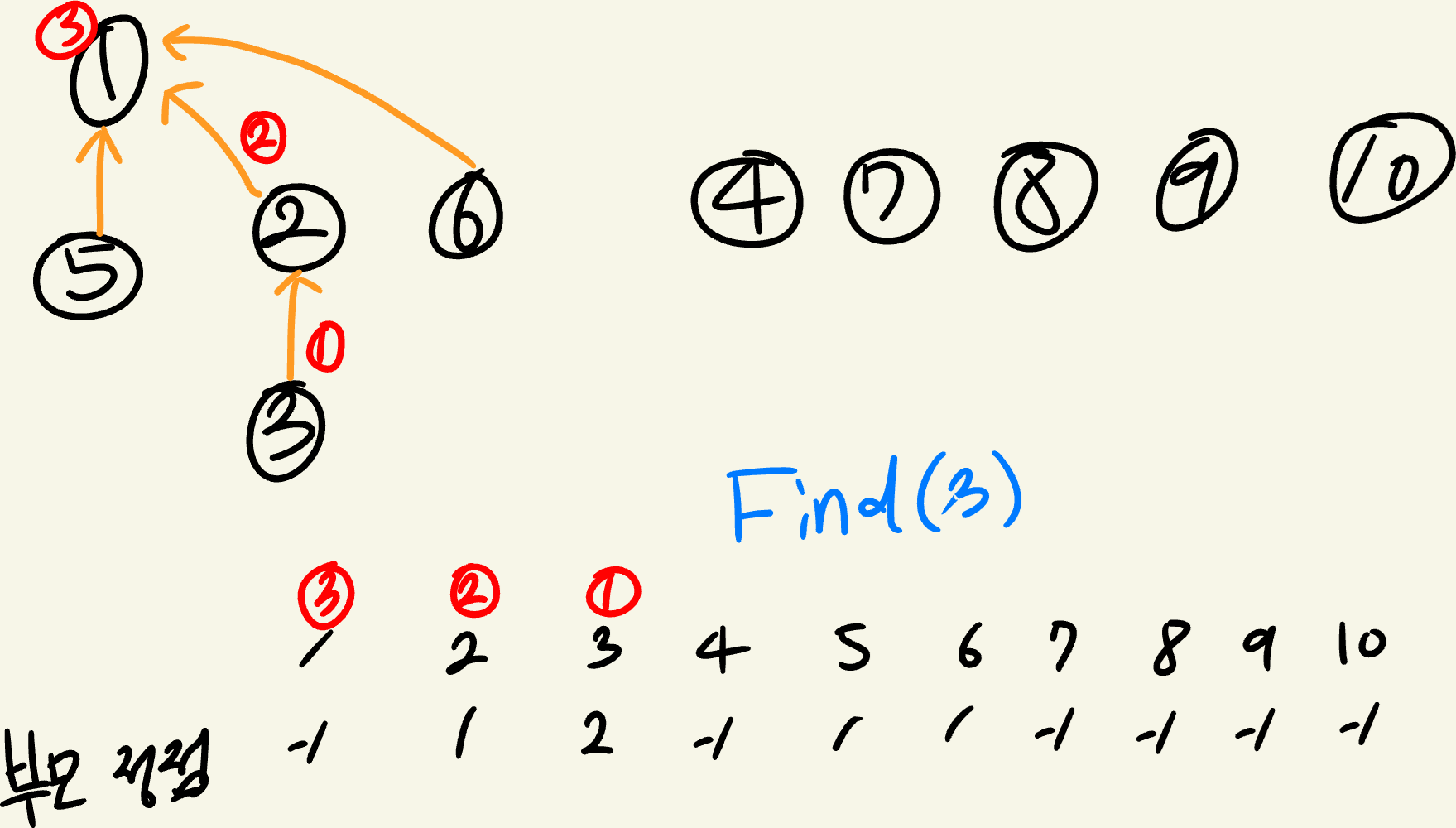
3을 탐색한다고 하면 3부터 시작해서 3의 부모(2) -> 2의 부모 -> ...
이렇게 루트노드까지 반복하여 find를 진행한다.
최적화
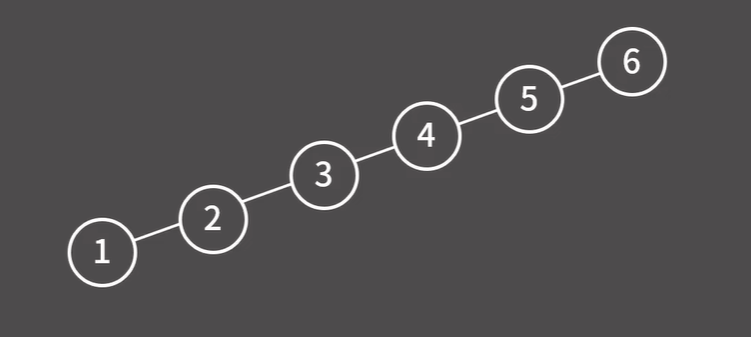
근데 union-find도 트리가 편향되는 경우 이 될 수 있다.
이를 방지하기 위해 2가지 방법이 존재한다.
-
Union by Rank
-
Path by Compression
Union by Rank
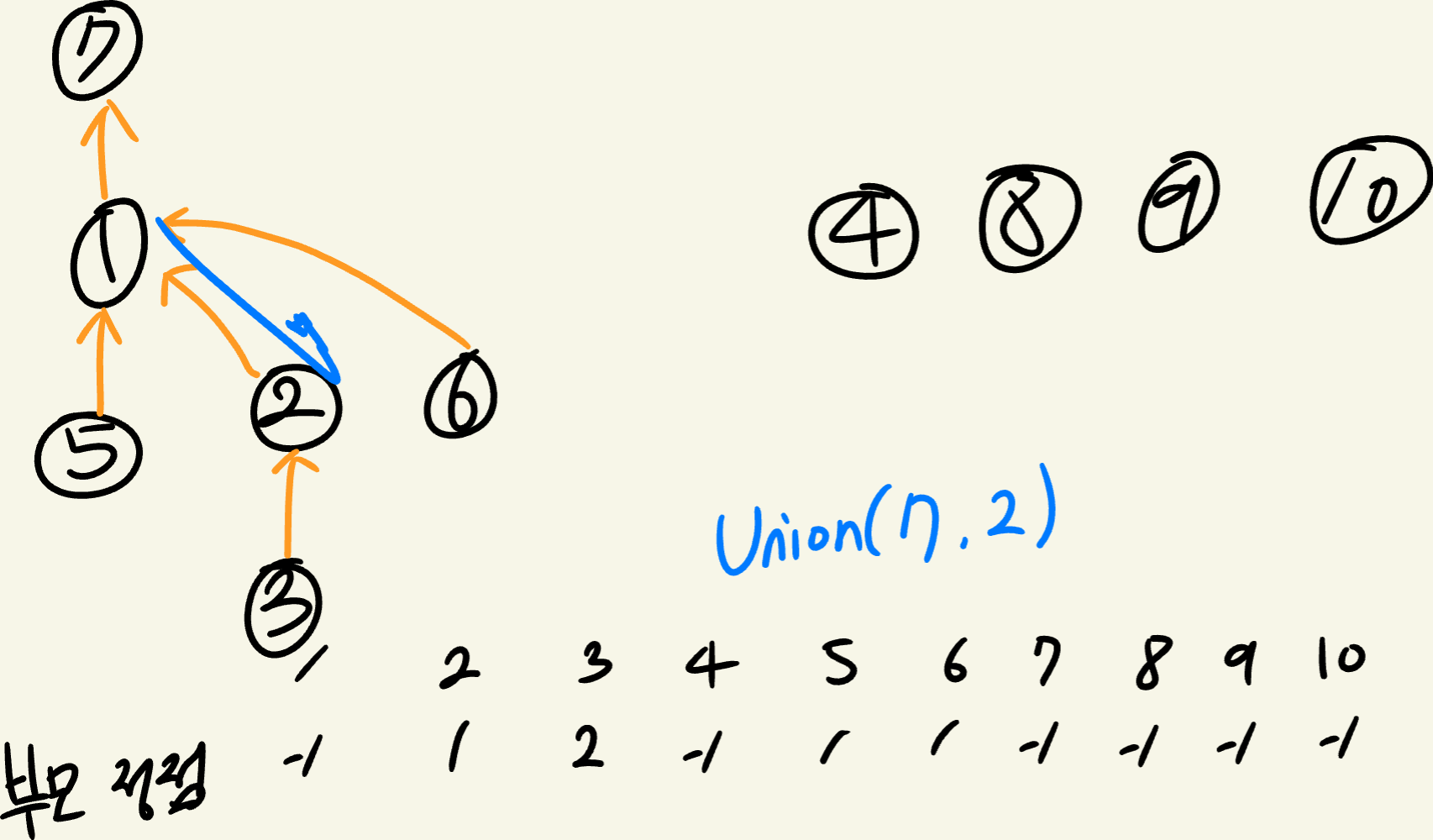
기존 방식대로 Union(7, 2) 를 한다면 2의 부모인 1을 7의 자식으로 만들게 된다.
하지만 트리의 높이를 최대한 낮추는게 실행 시간 면에서 유리한데
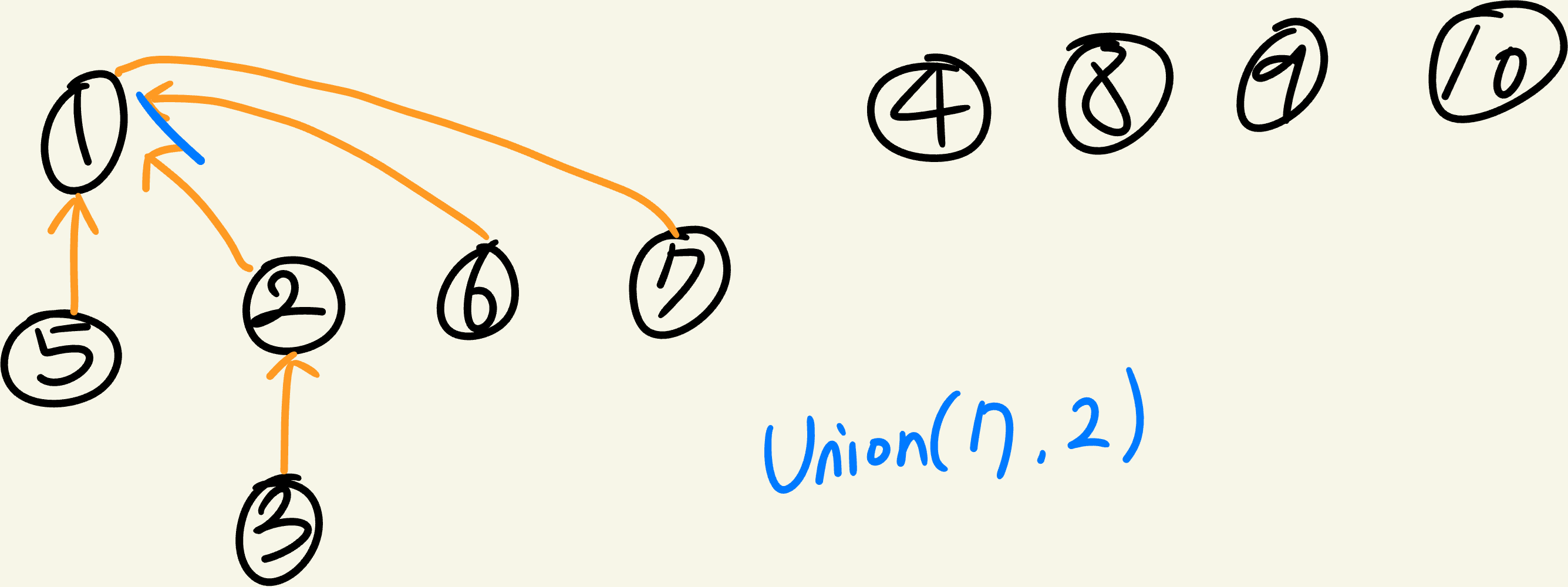
이렇게 하면 된다.
즉, 트리의 높이를 관리하기 위해 각각의 node에 대해 해당 tree를 root로 가지는 (rooted)subtree의 height를 rank라 정의해서 union by rank 방법이다.
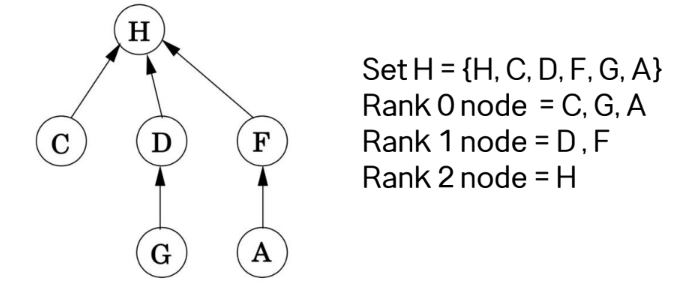
예시
- makeset(x): 단일 element x로 이루어진 set을 하나 생성한다.

는 x의 parent node이다.
(makeset은 동일하다.)
- find(x): x가 포함된 set을 return한다.
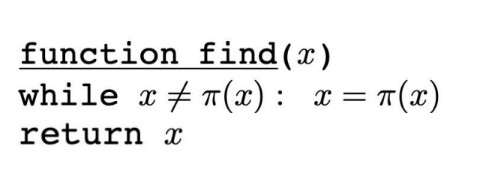
(find도 동일하다.)
- union(x)
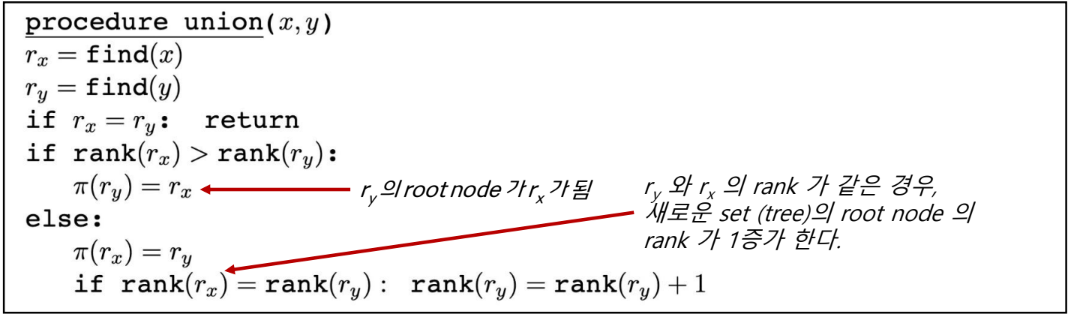
-
두 set을 포함한 root node 중 rank가 작은 root node의 parent가 rank가 큰 node의 root node가 되도록 조정한다. (같은 경우는 상관 없음)
-
따라서 두 set의 root node의 rank가 같지 않은 이상 union 후 새로운 root node의 rank는 변하지 않는다.
(같은 경우엔 1증가)
union 진행 예시
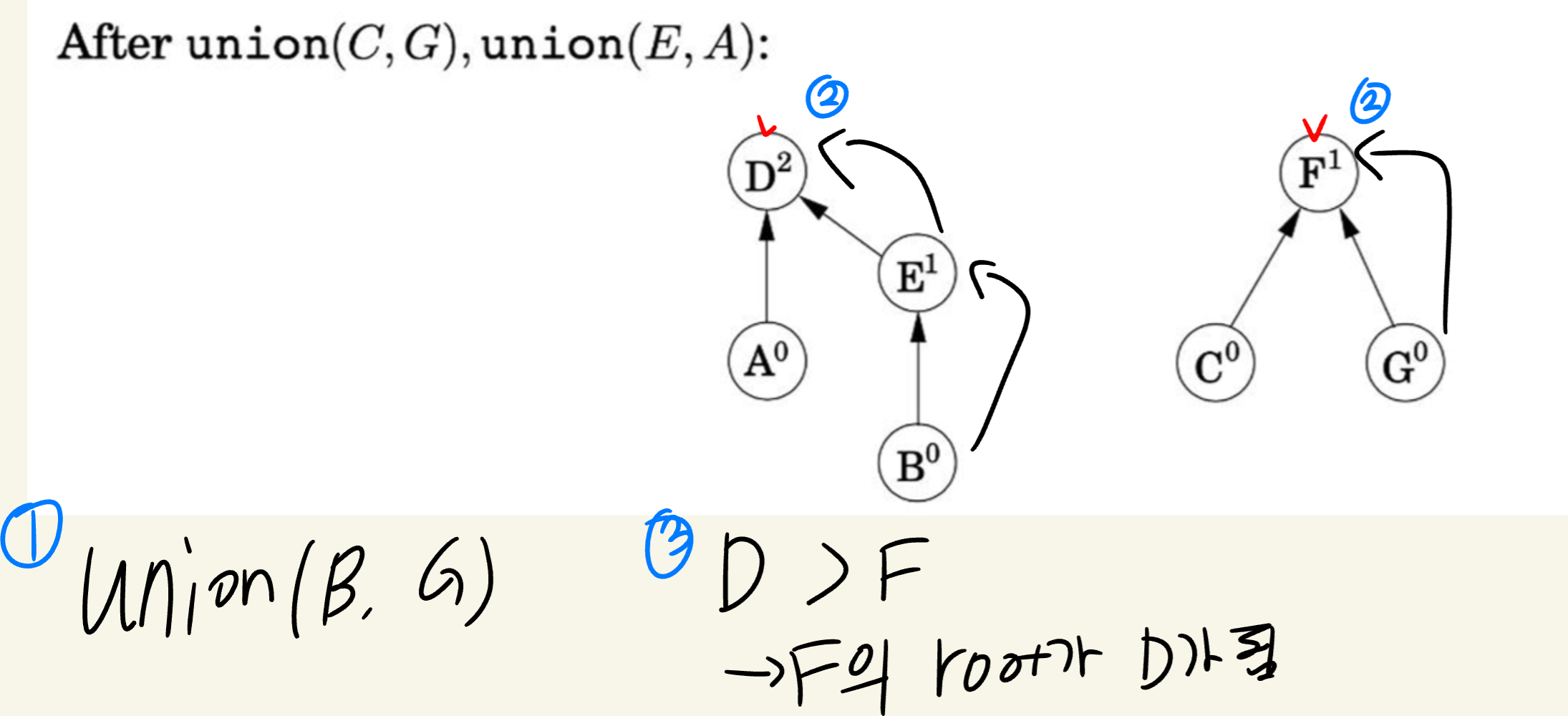
이렇게 union을 시킬 때 root 노드의 rank를 비교한다.
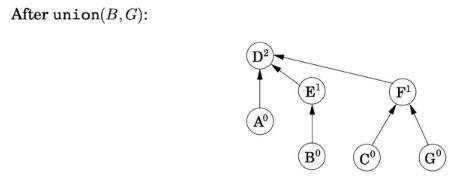
Path by Compression
union이나 find나 결국 find가 bottleneck이다.
따라서 find 를 할 때마다 나중에 나올 find 연산을 더 빠르게 지원할 수 있도록 tree 의 구조를 바꿔주는 것이 Path by Compression의 핵심이다.
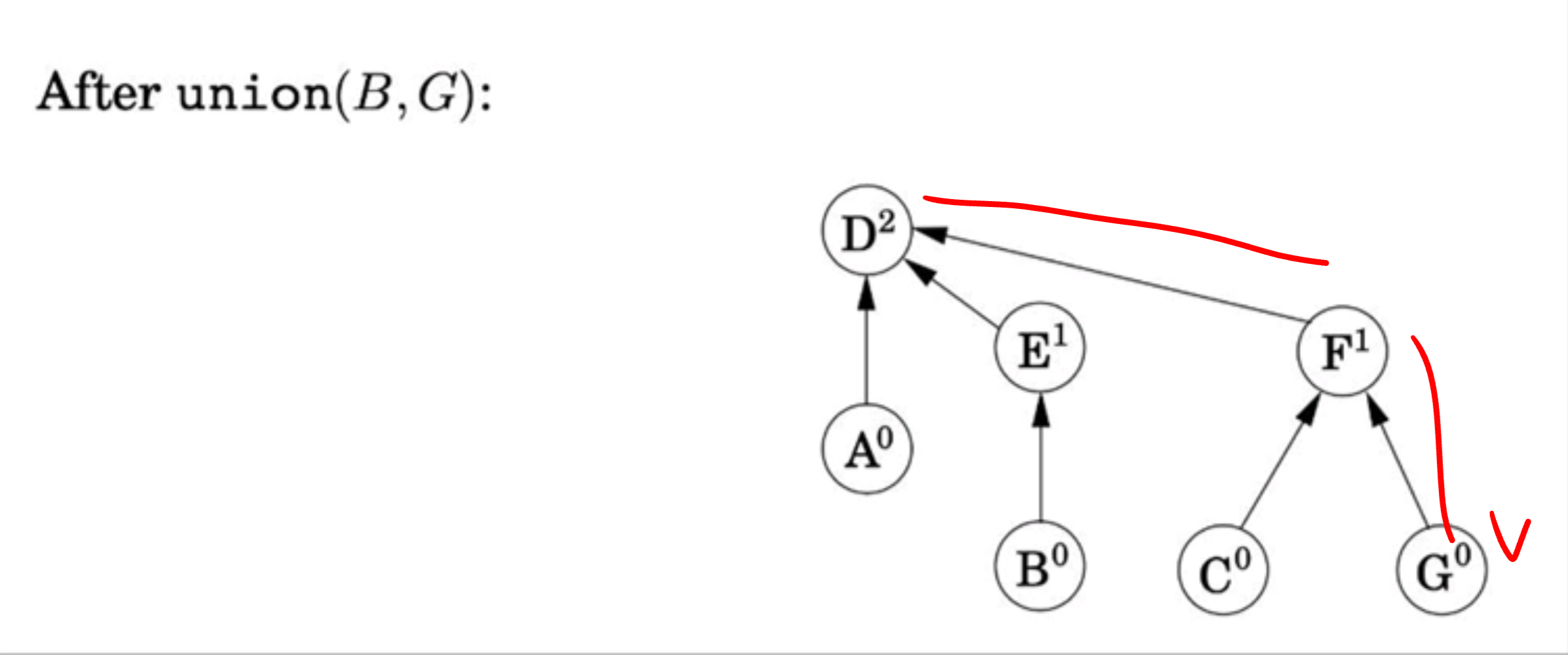
현재 find(G)를 진행하면 루트에서 F를 거쳐가야한다.
하지만 find(G)를 1회 진행하고 나면
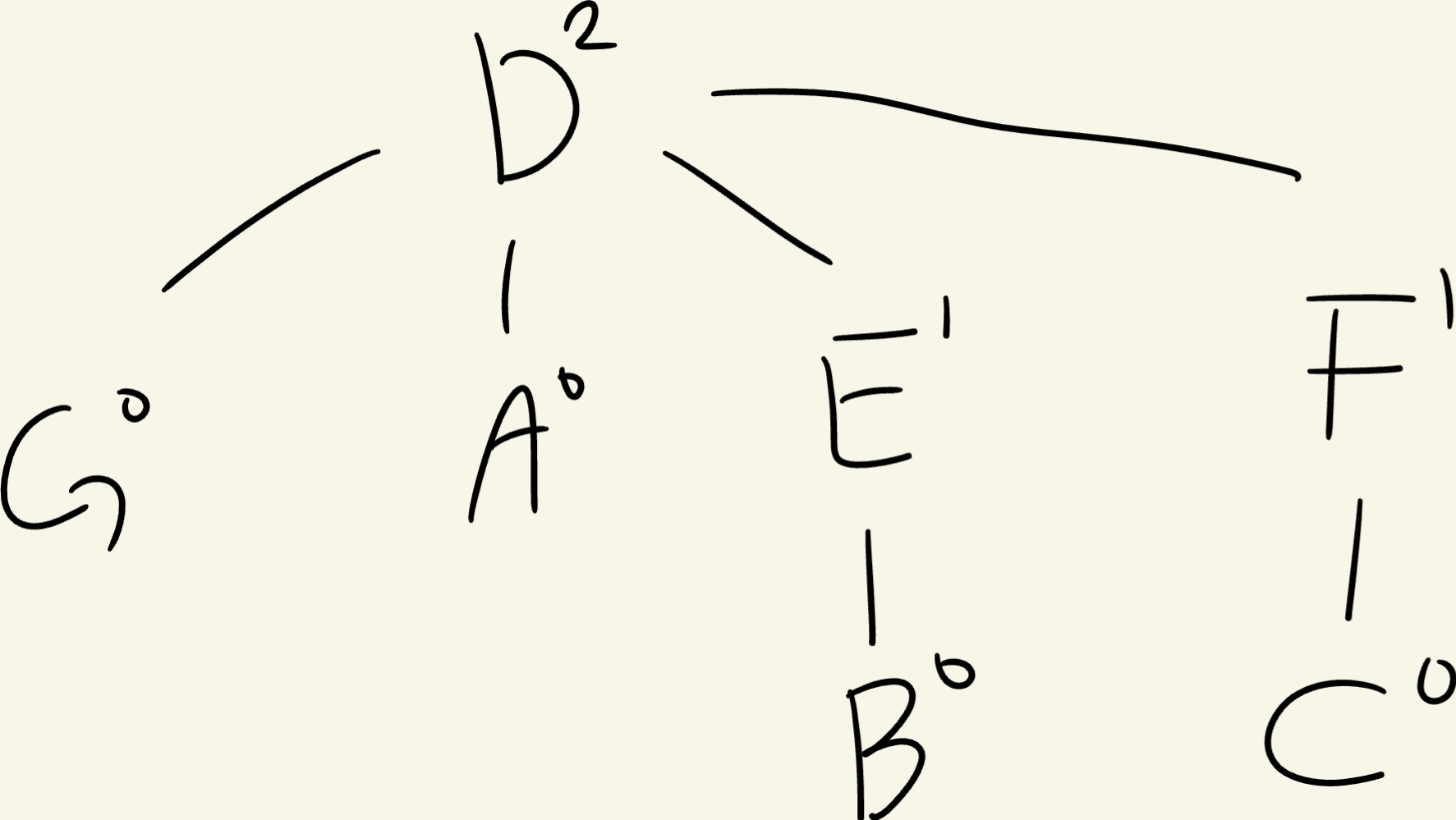
이렇게 G의 위치를 변경해준다.
-
find를 한 번 하고 나면 지나간 경로의 node를 root와 direct로 연결한다.
-
다만 rank는 update하지 않는다.
rank를 update하지 않는 이유
-
find와 union에서 병목 현상을 줄이고자 경로를 압축하는 것인데,
랭크를 정확히 맞추겠다고 남은 자식들을 다 검사() 하면 배보다 배꼽이 더 커지게 된다. -
랭크(Rank)는 "높이의 상한선(이 정도보다 높지는 않아)" 정도의 의미만 있어도 Union 연산을 효율적으로 하는 데 충분하기 때문이다.
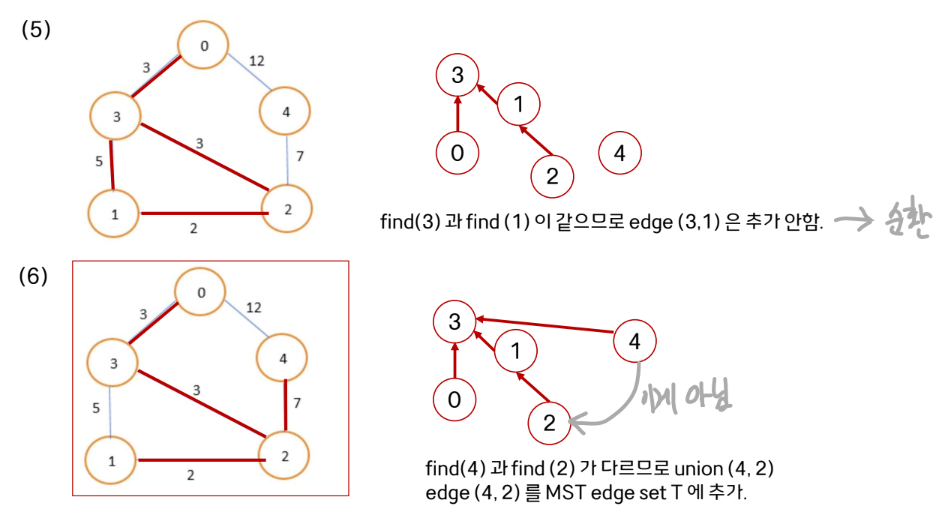
Kruskal's algorithm using uion-find
크루스칼 알고리즘에 union-find를 적용하면 더 빠르게 implementation할 수 있다.
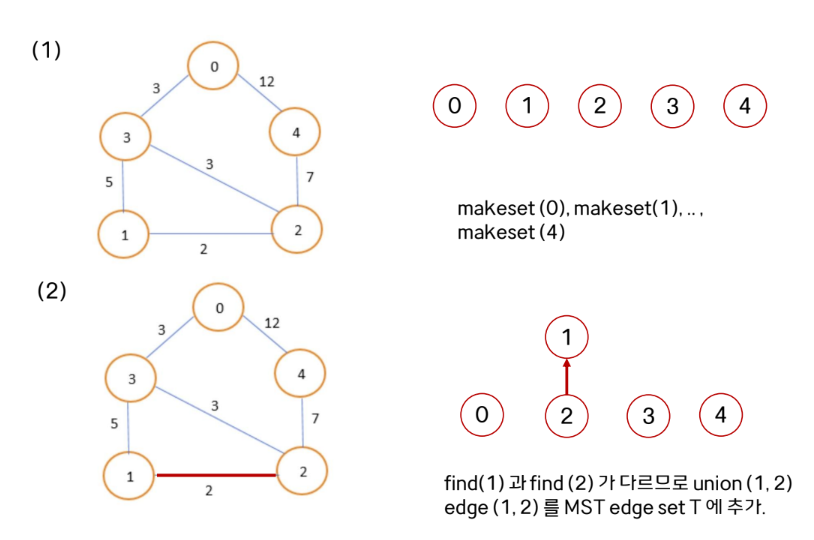
선택된 노드를 union해준다.
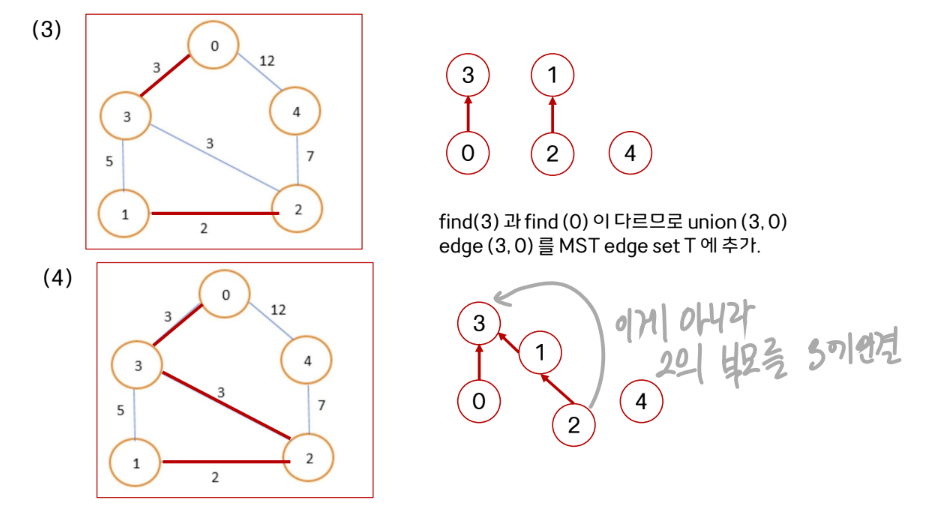
그리고 여기서 2와 3을 연결해줄 때 union(2, 3)으로 진행한다.
이렇게 크루스칼 알고리즘을 구현하면 기존 시간 복잡도인
가 아닌 이 나오게 된다.

⬇️

참고 자료
Algorithm [#6-1 Greedy Algorithms(1)] Chungbuk National University School of Computer Science Prof. Lee, Euijong
https://www.youtube.com/watch?v=rE-OUyZJgOk&list=PLtqbFd2VIQv4O6D6l9HcD732hdrnYb6CY&index=36
https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
https://ratsgo.github.io/data%20structure&algorithm/2017/11/12/disjointset/