[논문 리뷰]Safe Bipedal Path Planning via Control Barrier Functions for Polynomial Shape Obstacles Estimated Using Logistic Regression

선우진·2023년 11월 10일

Abstract

기존의 RRT 또는 RRT＊는 종종 보행 로봇의 동역학적 제약을 따르지 않는 경로를 생성합니다. 본 논문에서는 제어 장벽 함수(CBF)를 RRT/RRT＊에 통합하여 동적으로 실행 가능하며 충돌이 없는 경로를 합성합니다. 이는 기존 모델과 달리 로지스틱 회귀를 사용하여 환경의 그리드맵에서 불규칙한 모양의 장애물을 나타내기 위한 다항식 장벽 함수를 구성하는 방법을 도입했습니다. 더불어, 자유 공간 탐색의 효율성을 보장하기 위해 다단계 CBF 조향 컨트롤러를 개발했습니다.

I. INTRODUCTION

2D 복잡한 환경에서 안전한 경로 계획을 위한 수정된 CBF-RRT＊리즘을 개발하였습니다. 제안된 작업의 주요 기여는 다음과 같습니다. 첫째, 복잡한 장애물을 나타내기 위해 다각형 모양을 사용하는 장벽 함수를 구성하기 위해 로지스틱 회귀를 사용하는 새로운 방법을 제안했습니다. 둘째, 샘플링 및 한 반복 단계를 이동할 때 CBF-QP를 한 번만 계산하는 대신 한 단계를 네 개의 작은 단계로 나누어 계획 속도와 경로 안전성 사이의 효과적인 균형을 유지할 수 있습니다. 마지막으로 수정된 CBF-RRT＊ 알고리즘을 이족 보행 로봇에 적용하여 복잡한 장애물과 도달 불가능한 영역이 있는 방에서 안전하게 이동할 수 있도록 했습니다. 제안된 알고리즘은 실험실에서 Digit 로봇에서 평가되었으며 양다리 보행 로봇의 안전한 이동을 시연하였습니다.

II. BACKGROUND

CBF의 배경과 RRT/RRT＊ 기반 계획 알고리즘과의 통합을 검토합니다.

제어 장벽 기능을 RRT＊와 통합하여 장애물 회피를 보장하는 이족 보행 로봇의 안전한 경로 계획 알고리즘을 제시합니다. 또한 환경의 평면 그리드 맵에서 로지스틱 회귀를 사용하여 복잡한 장애물이나 도달할 수 없는 영역을 나타내는 다항식 장벽 함수를 구성할 것을 제안합니다. 마지막으로 상태가 안전하지 않은 세트로 끝날 수 있는 실행 불가능 문제를 해결하기 위해 다단계 CBF 조정 알고리즘을 개발합니다.

A. Bipedal Path Planning with Simplified Model

이 연구에서는 이족 보행 로봇이 안정된 저수준 이동 제어를 따르며 장애물이 없는 경로를 찾는 것을 목적으로 합니다. 로봇을 간단한 질량체로 가정하며, 웨이포인트나 속도 명령을 따를 수 있는 안정적인 이동 제어가 가능하다고 가정합니다. 양다리 로봇은 모든 방향으로 걷긴 할 수 있지만, 본 논문에서는 전진 걷기와 회전만을 고려합니다.

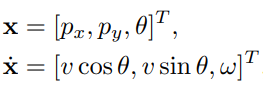
여기서 (px, py, θ)는 세계 좌표계에서 로봇의 위치와 진행 방향을 나타내고, (v, ω)는 로봇의 전진 속도와 각속도를 나타냅니다. v가 상수라고 가정하면 로봇 시스템은 다음과 같이 단순화될 수 있습니다.

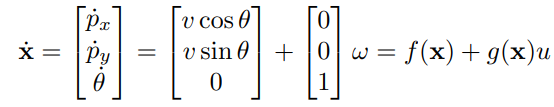
제어 입력은 u = ω입니다. 장애물과의 충돌을 피하기 위해서는 로봇을 장애물로부터 안전하게 멀어지게 하는 각속도 명령을 합성해야 합니다.

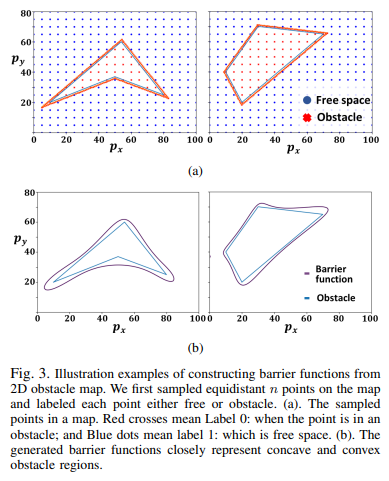
B. Construct Polynomial Barrier Functions via Logistic Regression from 2D Obstacle Map

이 논문에서는 CBF를 사용하여 충돌을 피하기 위해 환경의 장애물 경계를 나타내는 일련의 장벽 함수 h(x)를 정의해야 합니다. 우리는 그리드 맵에서 다항식 모양의 장벽 함수를 자연스럽게 생성하기 위해 로지스틱 회귀를 제안합니다. 원형이나 타원 형태와 비교하여 다항식 형태는 임의의 모양의 장애물을 효과적으로 나타낼 수 있습니다. 자유 공간은 닫힌 모양의 외부로 정의되므로 CBF를 사용할 때 다각형은 장애물을 나타내는 데 사용할 수 있습니다.

로지스틱 회귀는 표준 확률적 통계 분류 모델로, 다른 레이블의 데이터를 분류합니다. 로지스틱 회귀의 결과는 하나의 데이터 샘플에 대한 레이블 1 또는 0에 속할 확률입니다. 이 논문에서는 Broyden–Fletcher–Goldfarb–Shanno (BFGS) 알고리즘을 사용하여 이진 교차 엔트로피 비용을 최소화하여 파라미터 β를 결정합니다.

우리는 2D 장애물 맵에서 장벽 함수를 구성하기 위해 로봇의 상태 변수 x로부터 변수 z 집합을 결정하는 첫 번째 단계입니다. 이 논문에서는 로봇 위치의 다항식 함수 세트를 선택하고 최대 차수가 4인 z를 제시합니다. 장벽 함수는 h(x) := βz로 주어지며, 이는 맵에서의 점유 영역을 둘러싸고 있습니다.

마지막으로 BFGS 방법을 사용하여 파라미터 β를 해결하여 장벽 함수를 구성합니다. 결과적인 두 가지 예시로는 볼록 및 오목 모양의 장애물의 장벽 경계가 나타나 있습니다.

C. CBF-QP Safe Steering Controller

이족 보행 로봇이 환경 내의 장애물을 피해 안전한 경로를 찾기 위한 알고리즘에 대해 설명하고 있습니다.

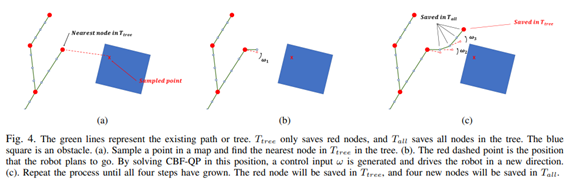
D. Implementation of the CBF-RRT* Algorithm

CBF-QP를 기반으로 한 RRT에서 스티어링 절차를 정의합니다. CBF-QP를 해결할 때마다 RRT에서 새로운 지점을 샘플링하는 과정에서 스티어링 절차를 구성합니다. CBF-RRT＊ 알고리즘에서 제시된 스티어링 방법과는 달리 이 알고리즘은 하나의 큰 단계를 네 개의 작은 단계로 분할하고, 각각의 헤딩은 CBF-QP를 해결하여 계산된 각속도로 제어됩니다. 제안된 다단계 스티어링 알고리즘은 경로 데이터를 저장하기 위해 두 개의 노드 목록이 필요합니다. 하나는 트리 노드 목록(Ttree)으로, 각 루프에서 트리가 한 바깥 반복을 성장한 후의 노드만 저장합니다. 다른 하나는 모든 노드 목록(Tall)으로, 트리가 한 바깥 반복 단계 동안 성장한 네 개의 모든 노드를 저장하며, 실제 동작 경로를 추적하는 데 사용됩니다. 먼저 맵에서 점을 샘플링하고 Ttree에서 가장 가까운 노드를 선택합니다. 그런 다음 샘플링된 점 방향으로 로봇이 이동할 수 있는 위치를 첫 번째 작은 단계로 삼아 그 CBF-QP를 해결하고, 이로 인해 새로운 노드로의 헤딩이 변경되고 로봇이 새로운 노드로 이동할 수 있습니다. 이러한 과정을 트리가 네 단계 모두 성장할 때까지 반복하고, 네 개의 새로 생성된 노드는 모두 Tall에 저장되며, 마지막으로 생성된 네 개의 노드는 Ttree에 저장됩니다. 이러한 방법을 도입함으로써 제안된 알고리즘은 CBF가 실행 불가능한 상황을 효과적으로 피하고 로봇의 안전을 유지할 수 있습니다. Tall 및 Ttree에 노드를 저장한 후 ChooseParent 및 Rewrite 방법을 사용하여 경로를 최적화하기 위해 노드의 부모를 변경합니다. 특히 이 두 가지 절차에서는 알고리즘의 계산 효율성을 향상시키기 위해 간단한 충돌 확인 함수를 사용합니다.

IV. SIMULATIONS AND HARDWARE EXPERIMENTS

A. Simulation Results

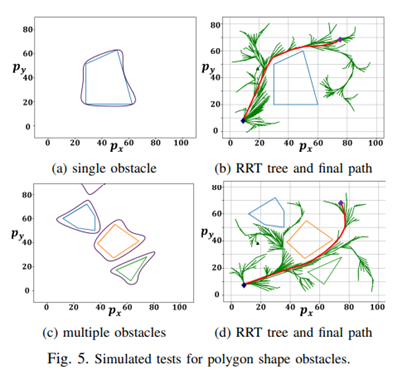
B. Hardware Experiments with Digit

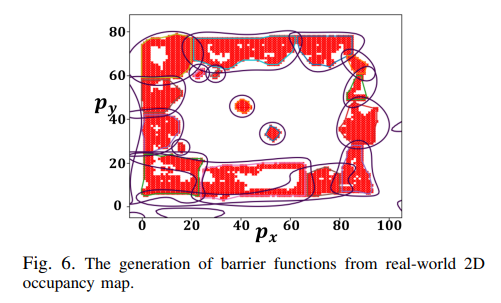
실험에서는 먼저 Depth 카메라 및 LiDAR에서 얻은 포인트 클라우드 데이터를 사용하여 방의 점유 맵을 생성했습니다. Random Sample Consensus 방법을 사용하여 포인트 클라우드를 세분화하여 장애물과 빈 공간을 구분했습니다. 그 결과 장애물 포인트는 2D 평면으로 투영되며, 투영된 포인트가 포함된 셀은 장애물로 간주됩니다. 장벽 함수를 효율적으로 생성하기 위해 지도를 여러 영역으로 나누고 각 영역에 대해 장벽 함수를 생성했습니다. 그림 6은 방의 점유 맵과 장애물의 생성된 장벽 함수를 보여줍니다. 이러한 장애물을 구성하는 데 걸린 시간은 3.03초입니다. 로봇의 시작 위치는 (6.5, 4.0)m이고 목표 위치는 (3.6, 3.0)m이며, 알고리즘을 15번 실행했습니다. 평균 시간 소요는 14.26초이며 평균 반복 횟수는 32.03입니다.
https://www.youtube.com/watch?v=r_hkuK5cMw4

V. CONCLUSIONS

복잡한 모양의 장애물에 대한 충돌 없는 경로를 생성할 수 있는 CBF-RRT＊의 새로운 프레임워크를 제안했습니다. 또한, 하드웨어 실험을 통해 알고리즘의 현실 세계 환경에서의 적용 가능성을 시연했습니다. 그러나 알고리즘은 일부 경우에는 여전히 충분하지 않습니다. 예를 들어, CBF를 생성하기에 공간이 너무 작은 장애물이 있는 경우나 그림 6과 같이 주변 장애물을 단일 CBF로 표현할 수 없는 경우 등이 있습니다. 향후 연구에서는 그래픽 및 기계 학습에서 개선된 알고리즘을 탐색하여 이러한 문제를 해결하고 실제 환경에서의 성능을 향상시킬 계획입니다. 또한, 알고리즘의 계산 효율성을 더욱 향상시켜 안전한 실시간 탐색에도 적용할 수 있도록 할 것이며, 양다리 로봇의 민첩성을 제한할 수 있는 차분 구동 모델에 대한 더 적절한 모델 표현을 탐구할 것입니다.