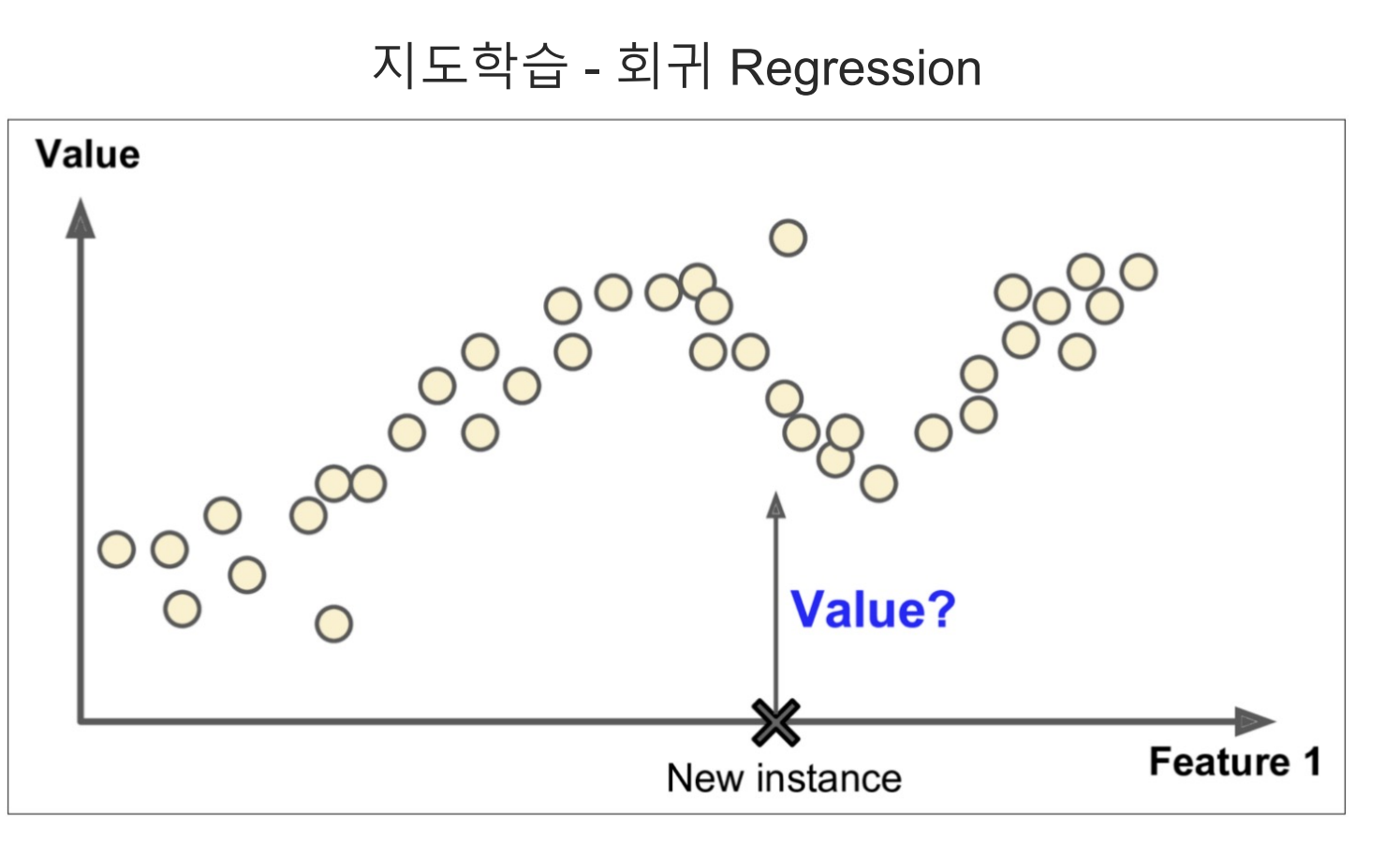
- 회귀에서 지도학습은 기존의 데이터를 통해 모델링을 한 후 새로운 Data를 넣었을 때 이를 예측하는 것이다. 함수와 비슷하다
- 일 때 에 넣는 값에 따라 출력이 달라지듯이
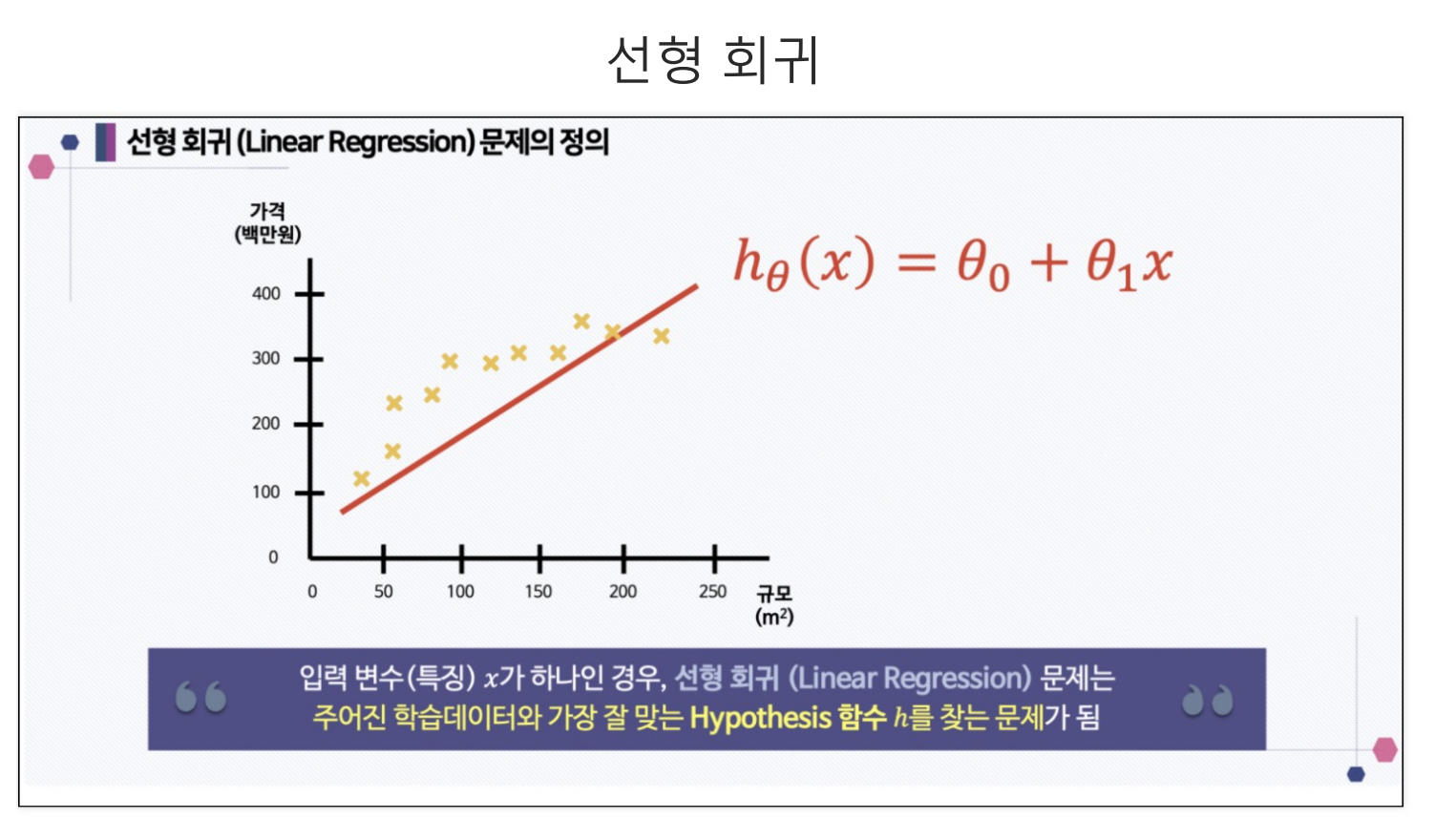
- 선형회귀의 경우 결국 1차식 함수의 방정식을 추론하는 것과 같다.
- 축이 label값이고, 에 넣는 값이 주어지는 Data라고 생각하면 이해하기 쉬울 것 같다.
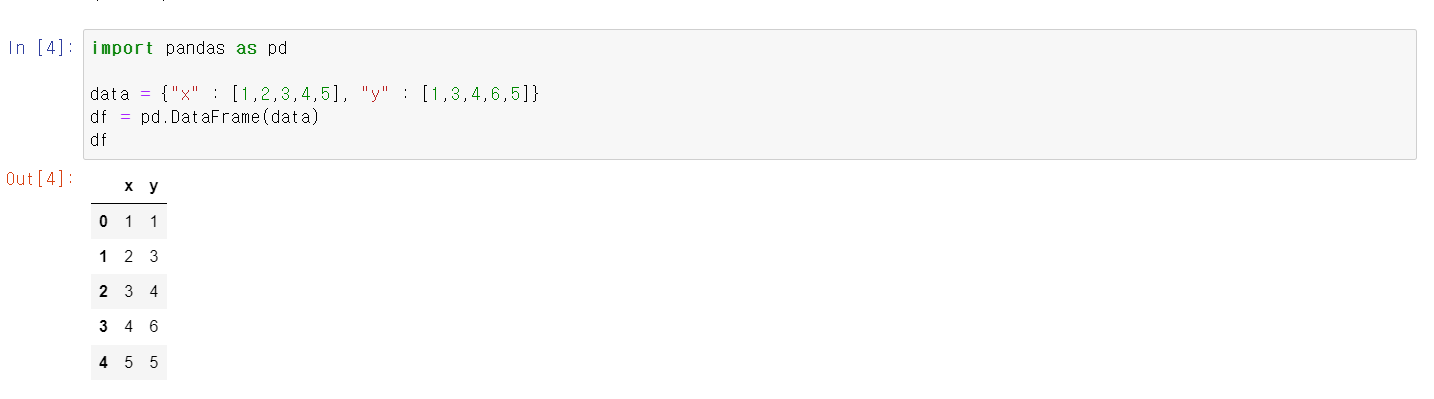
- 간단한 자료로 이해를 해보자
- 컬럼에 값을 넣고
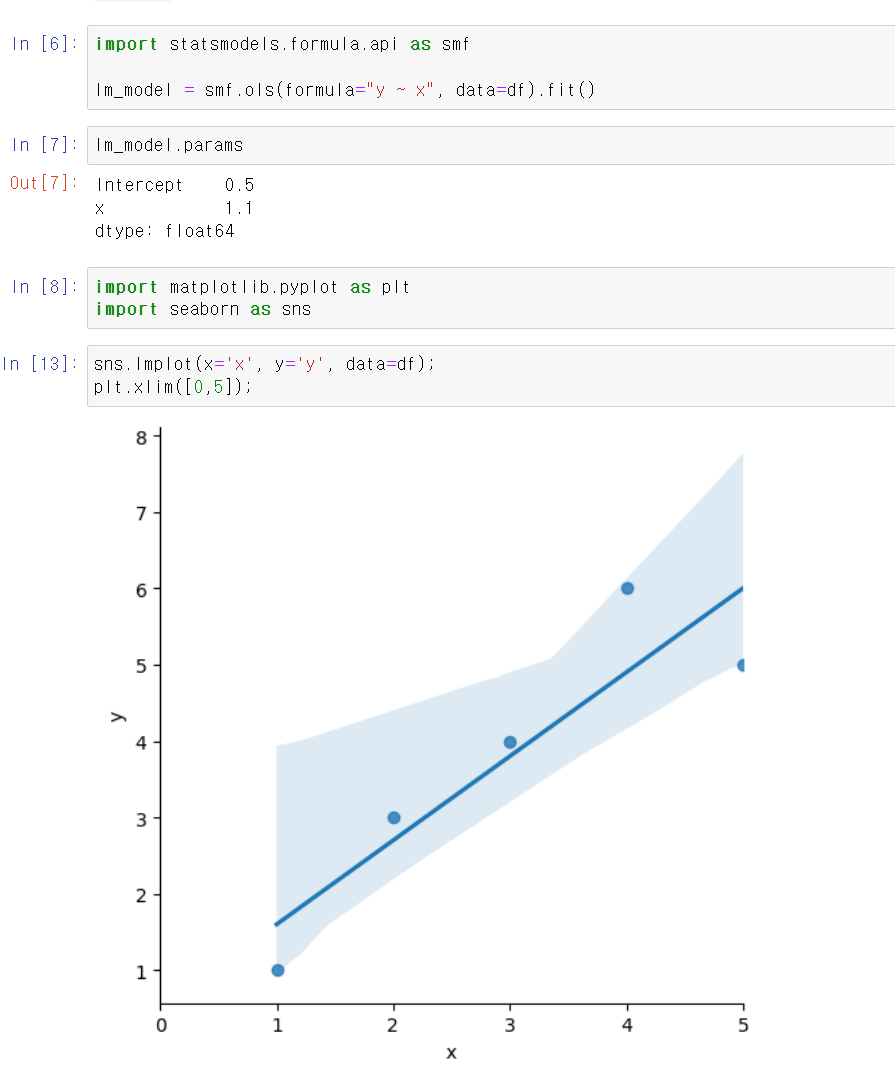
- statsmodels 모듈에서 간단하게 1차식 방정식을 구할 수 있는데 해당 값을 넣은 결과 의 값이 나왔다. 해당 값이 회귀직선의 방정식이다.

- 잔차는 실제값과 예측값의 차이로 이 차이를 나타내는 것이다.
- 위에 사용한 statsmodels를 통해 잔차 또한 간단히 확인할 수 있다.
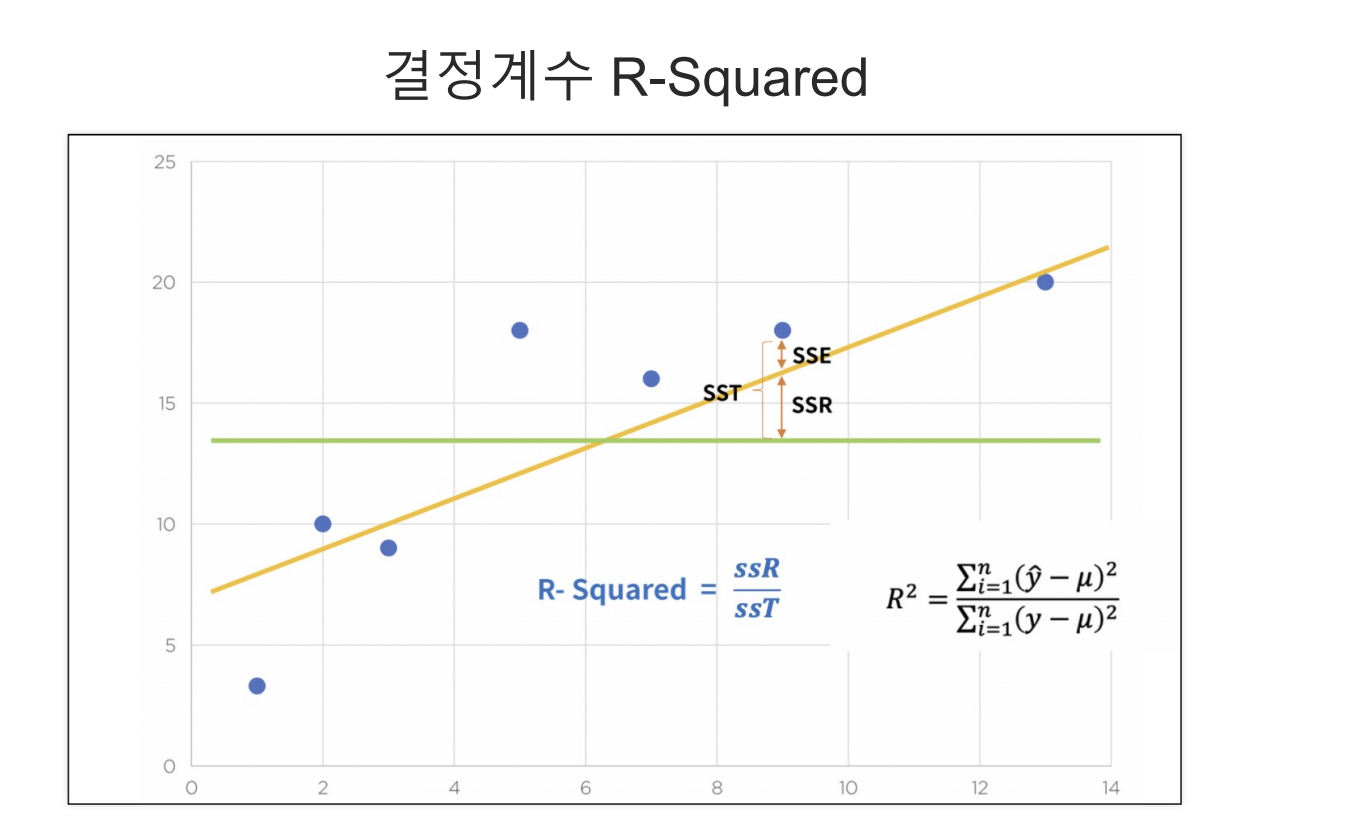
- 결정계수(R-Squared)는 사용한 회귀식의 성능을 나타내는 지표 중 하나로 사용된다.
- ssR은 이며, ssT는 인데, 이를 로 계산하면 결과가 나온다.
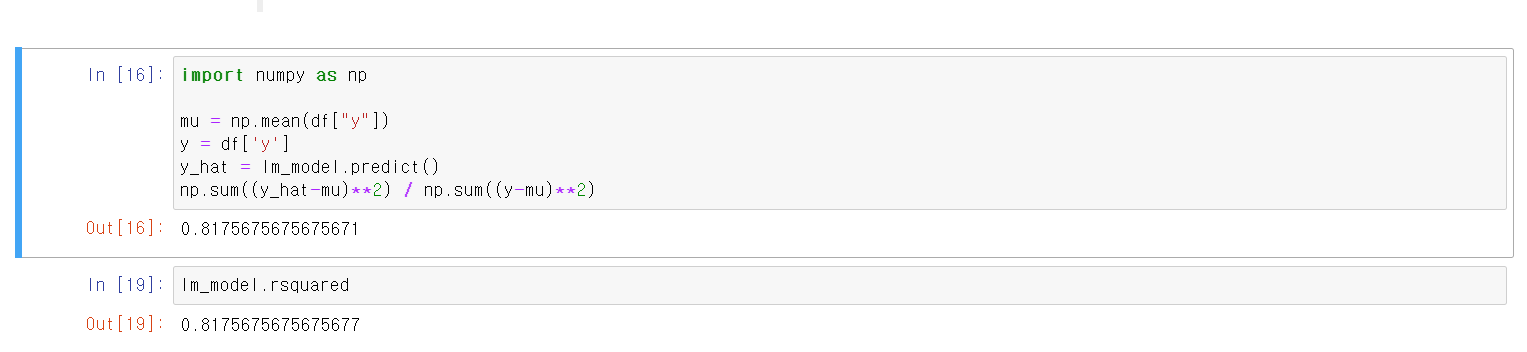
- 직접 수식을 넣어 구할 수도 있고, statsmodels에 기능을 사용해서 한 번에 값을 출력할 수도 있다.
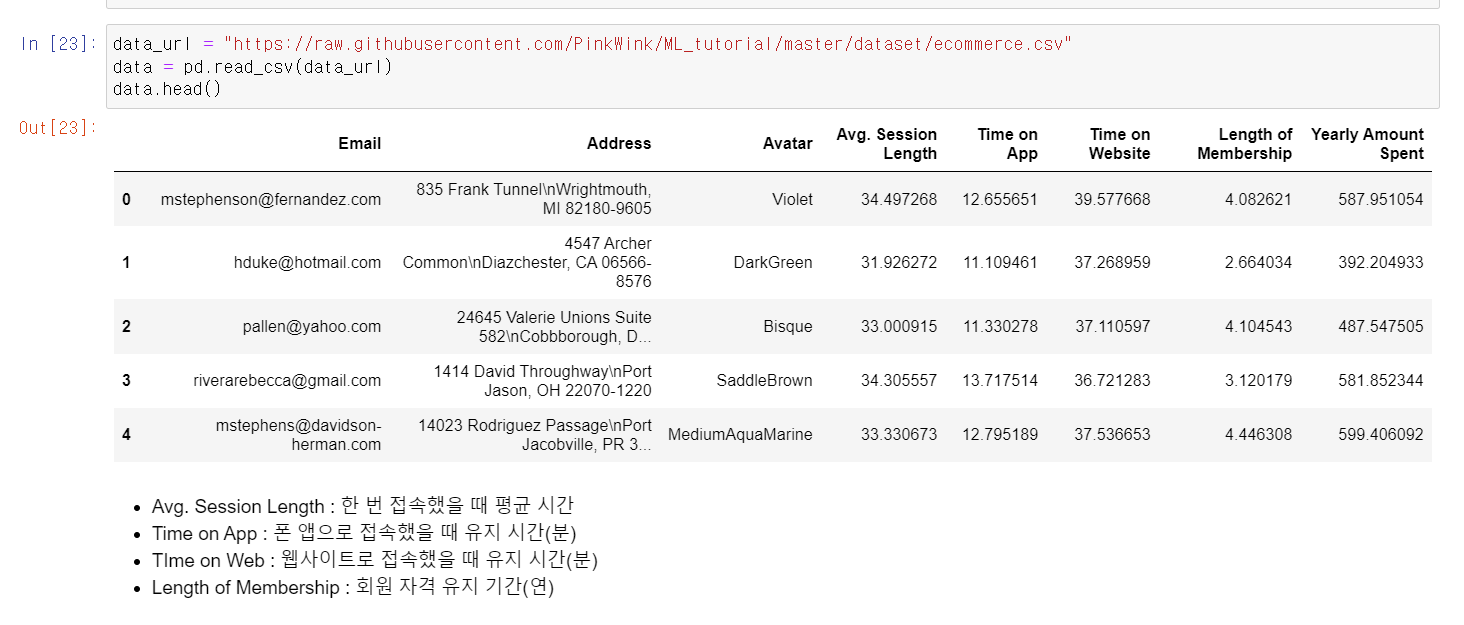
- 이제 직접 회귀분석을 해보자
- 먼저 이커머스 데이터를 저장한다.
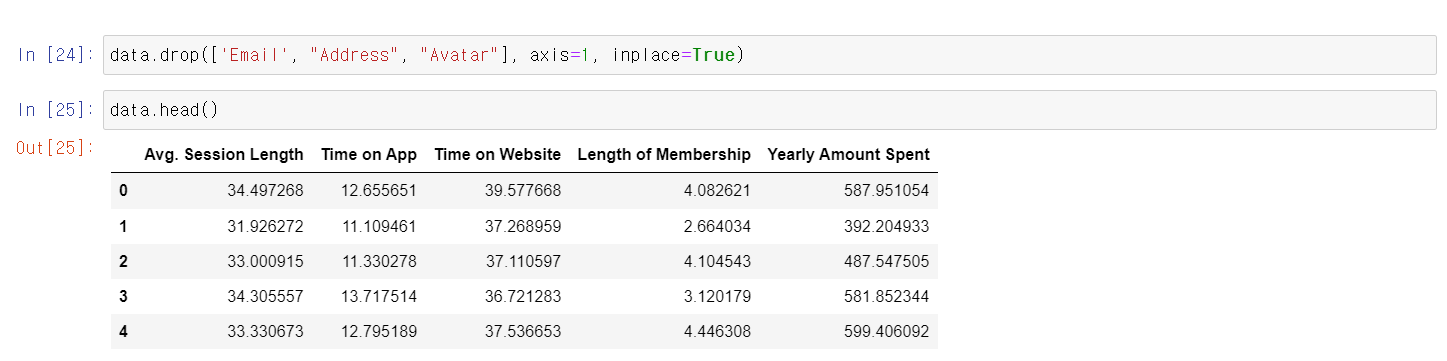
- 회귀분석을 위해 필요한 데이터만 빼고 나머지는 drop후 다시 확인한다.
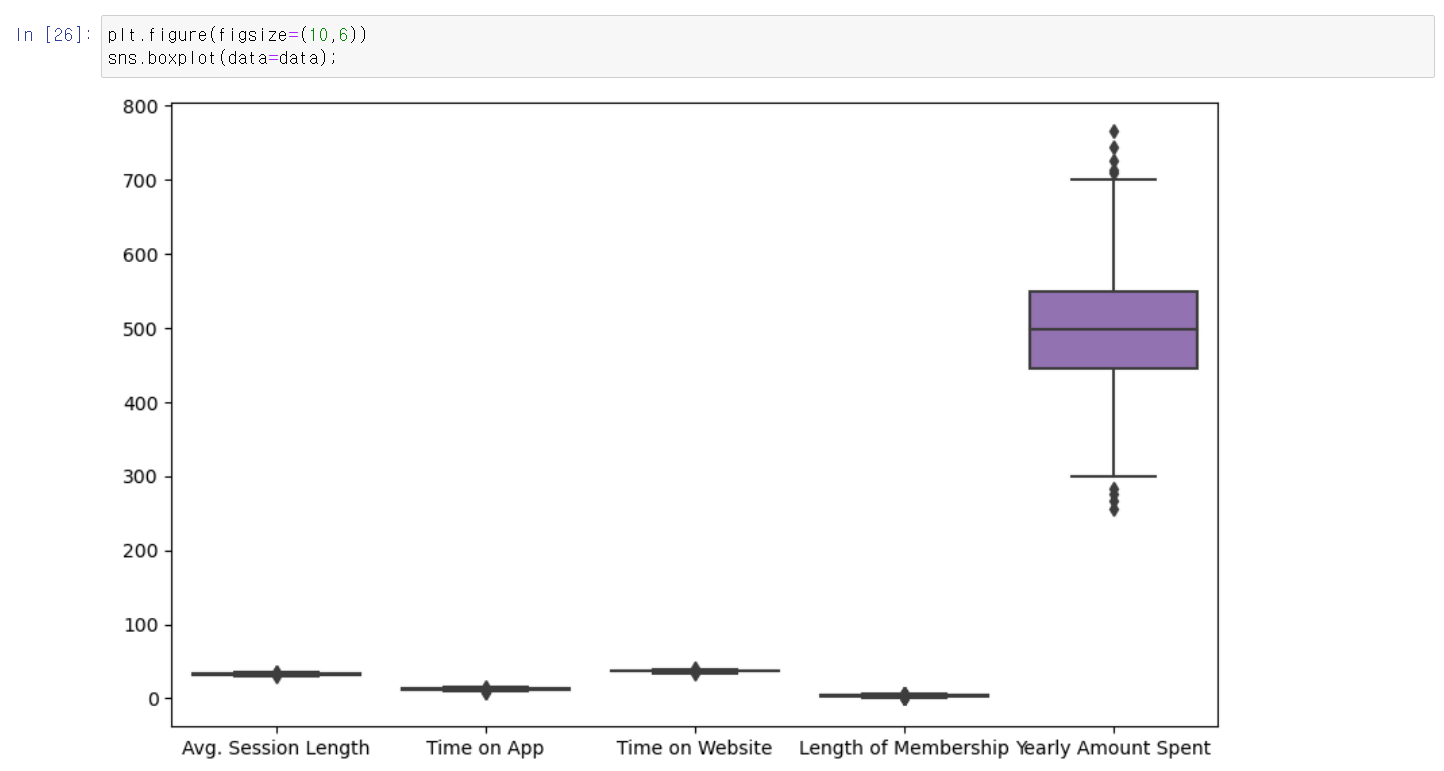
- 먼저 데이터를 분석하는데 Yearly Amount Spent변수값이 다른 변수값보다 수치가 높기에 제대로 분석하기가 힘들어
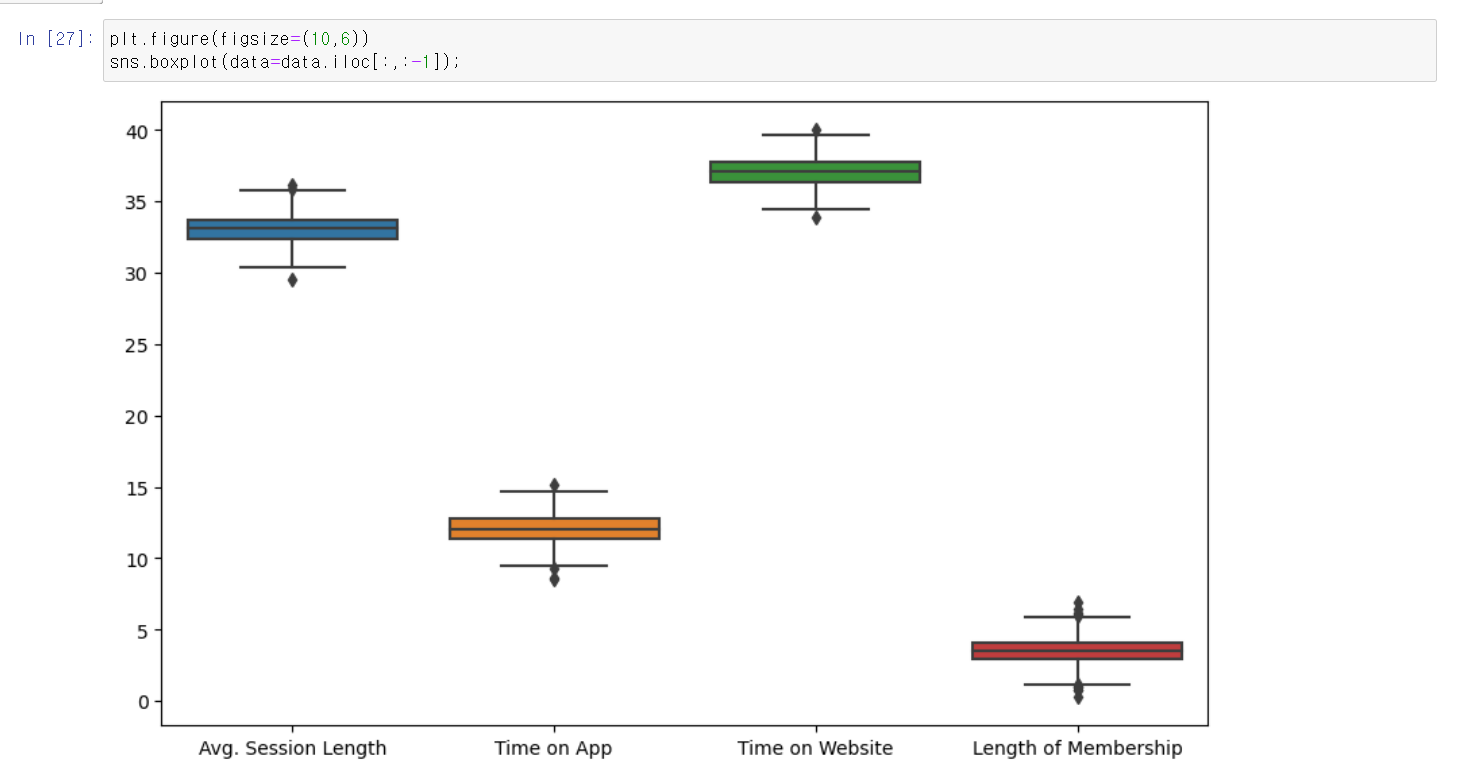
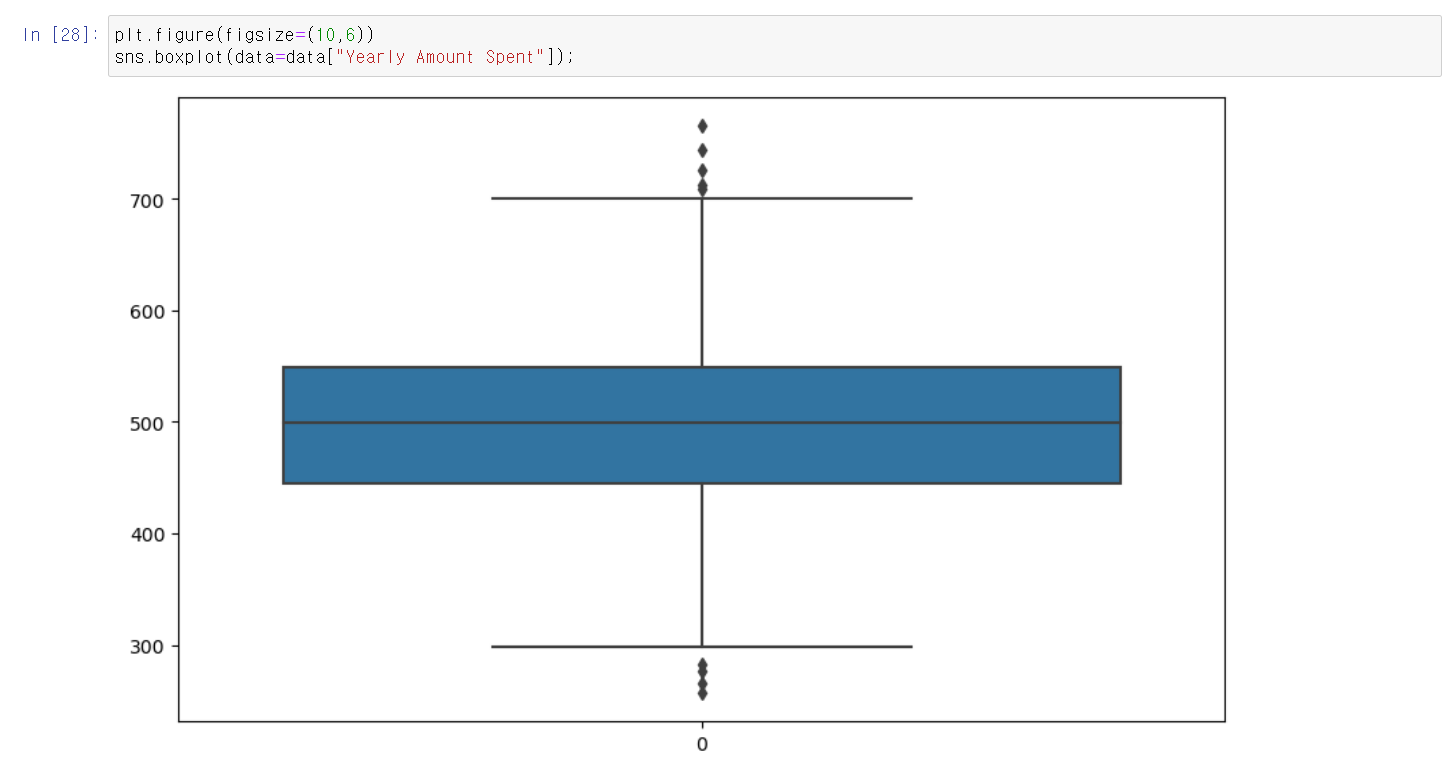
- 두 그래프로 따로 분석했다.
- velog를 작성하면서 다시 보니 위에 4가지 값을 통해 DecisionTree를 사용하면 간단하게 예측을 할 수 있을 것 같다는 생각이 든다.
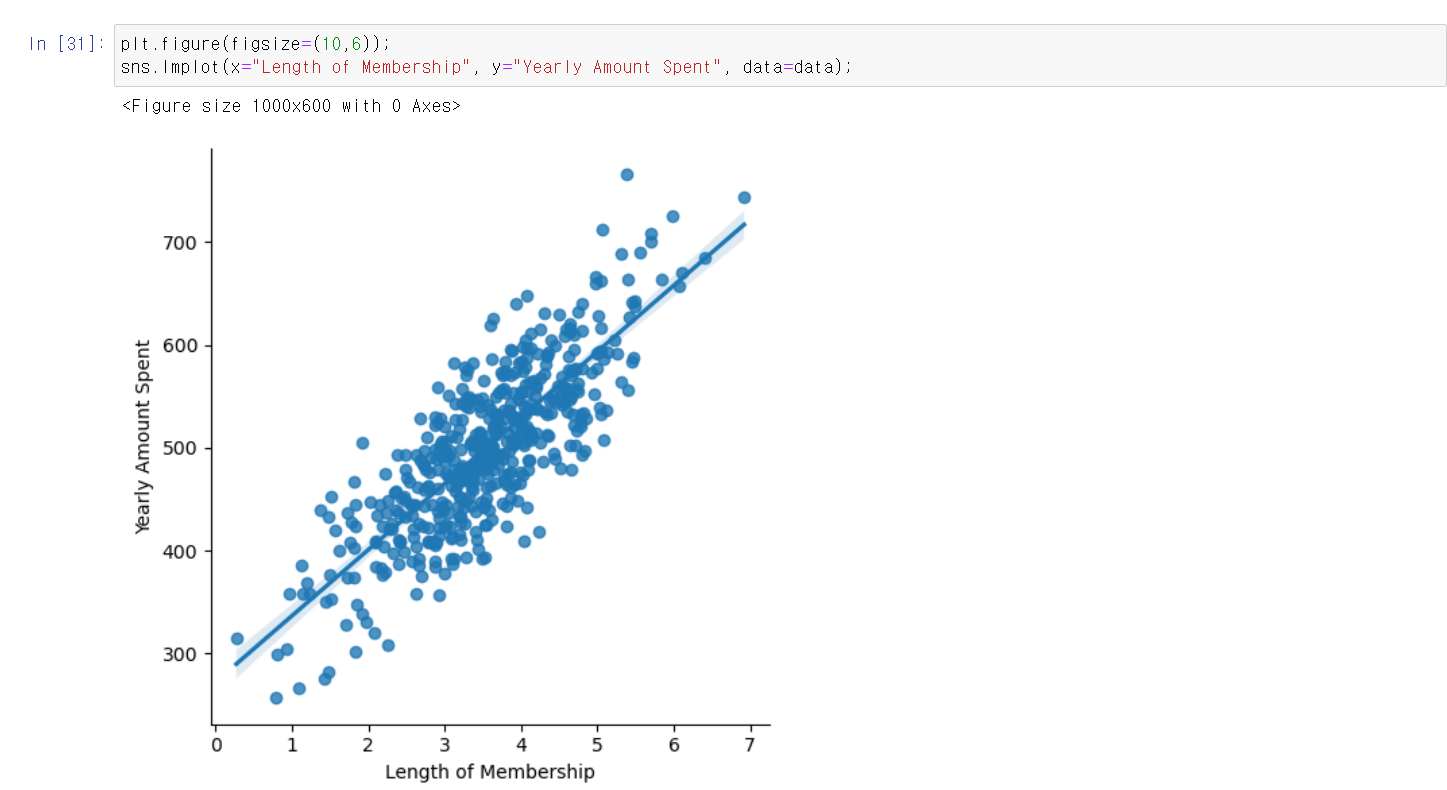
- 일단 목적은 회귀분석이니 가장 분석하기 좋은 두 변수값을 통해 시각화를 했다.
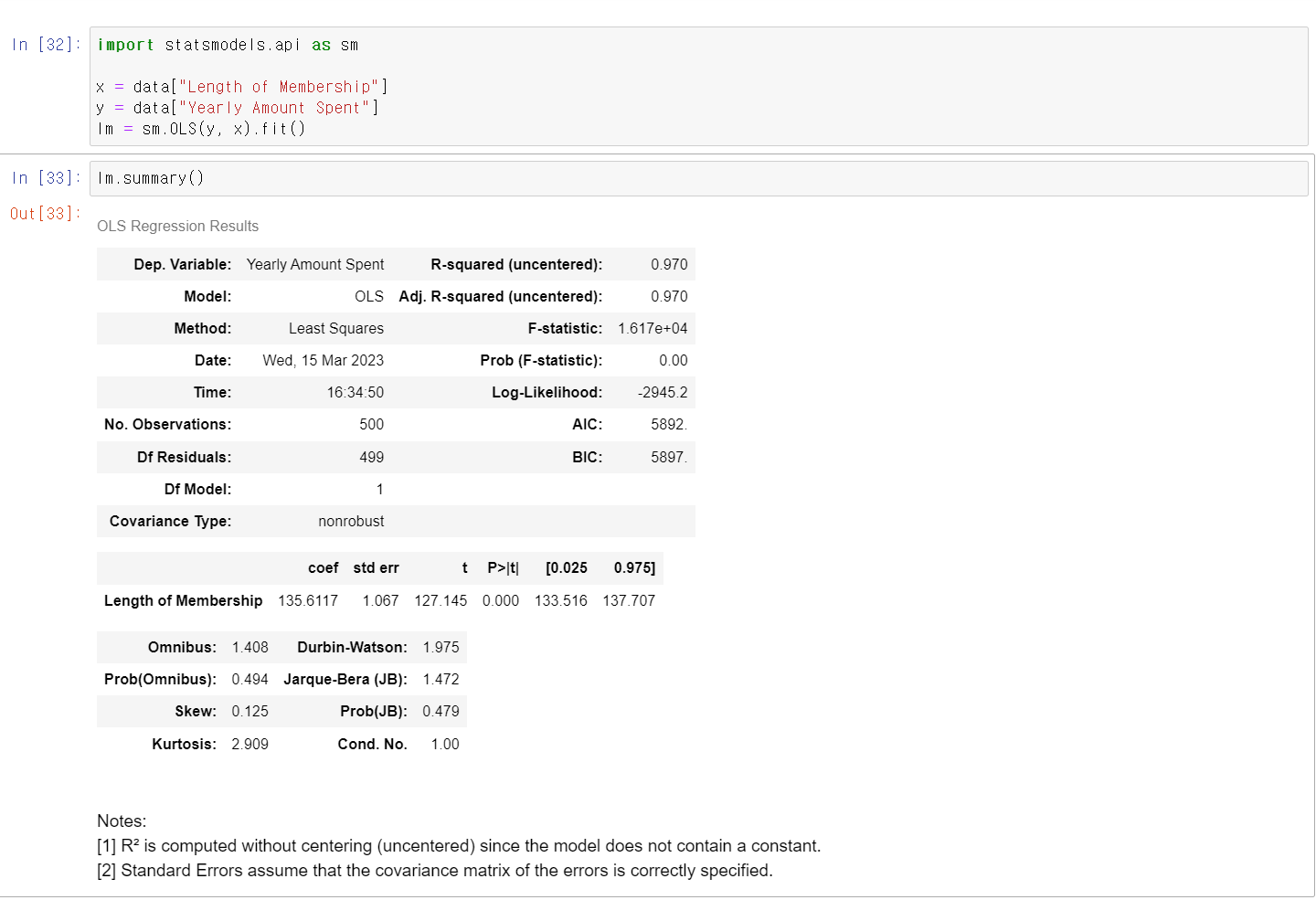
- 두 데이터를 OLS(Ordinary Least Squares)방식으로 회귀 모델링을 교육시켰다.
- 하지만 문제는 에 상수값을 입력하지 않아 제대로 모델링을 못했다.
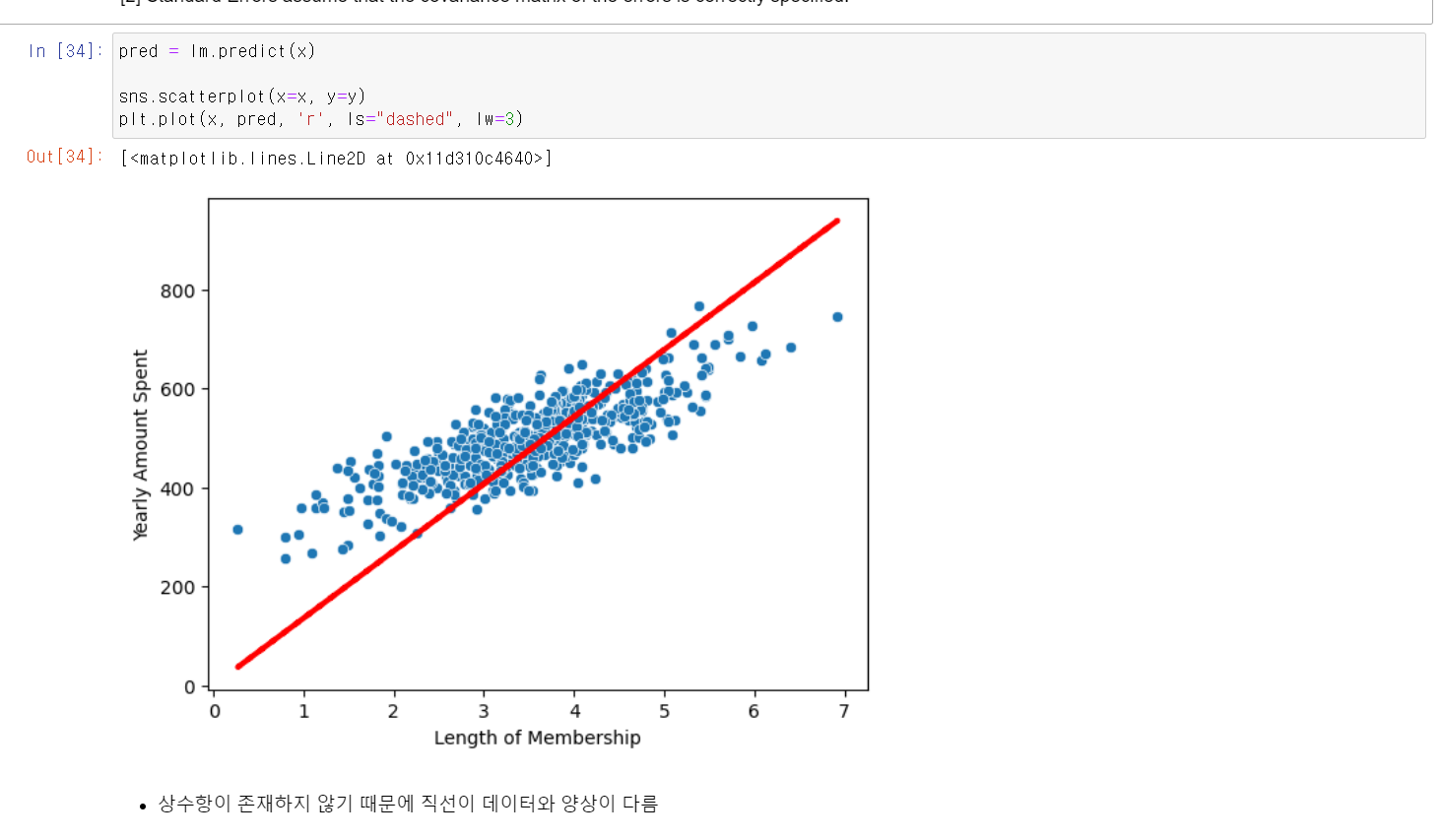
- 시각화를 통해 확인해보니 역시 회귀직선이 제대로 만들어지지 않았다.
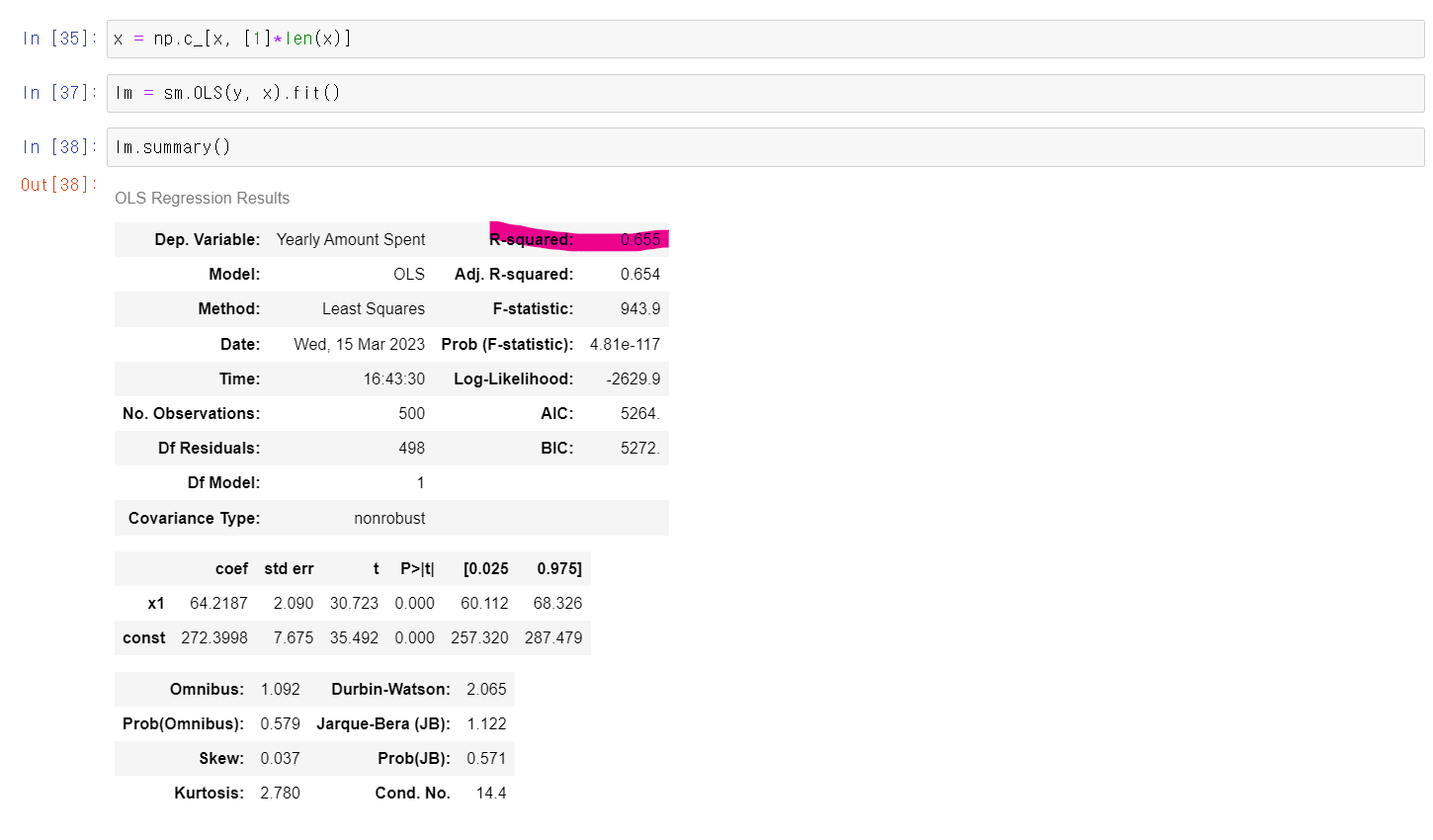
- 에 상수값 1를 넣고 다시 모델링을 해보니 R-Squred값은 다소 떨어졌다.
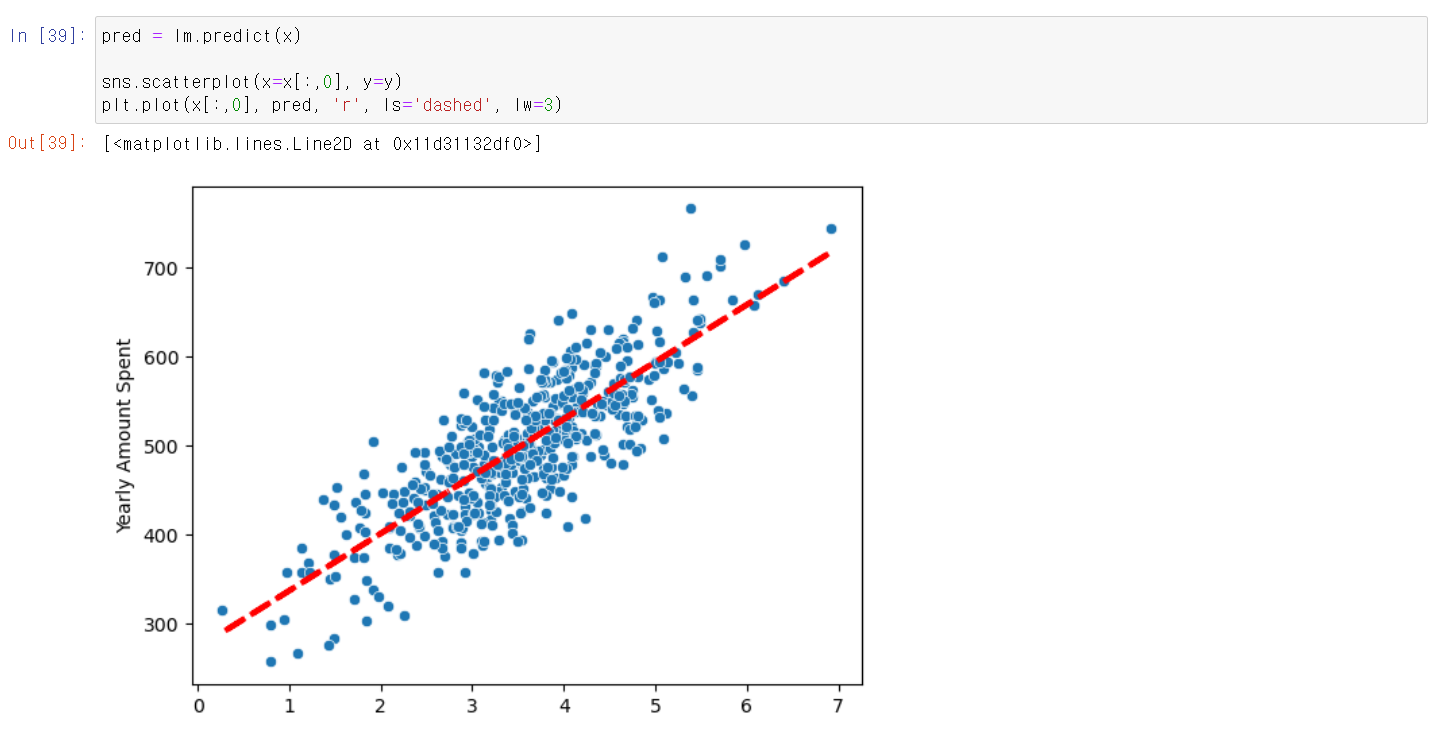
- 하지만 회귀직선은 데이터의 추세와 맞게 제대로 만들어졌다
- 여기서 중요한 점은 R-Squred값을 무조건적으로 믿어서는 안되겠다는 것이다.

- 이제 데이터를 8:2로 Train, Test데이터로 구분하고 다시 모델링을 시켰다.
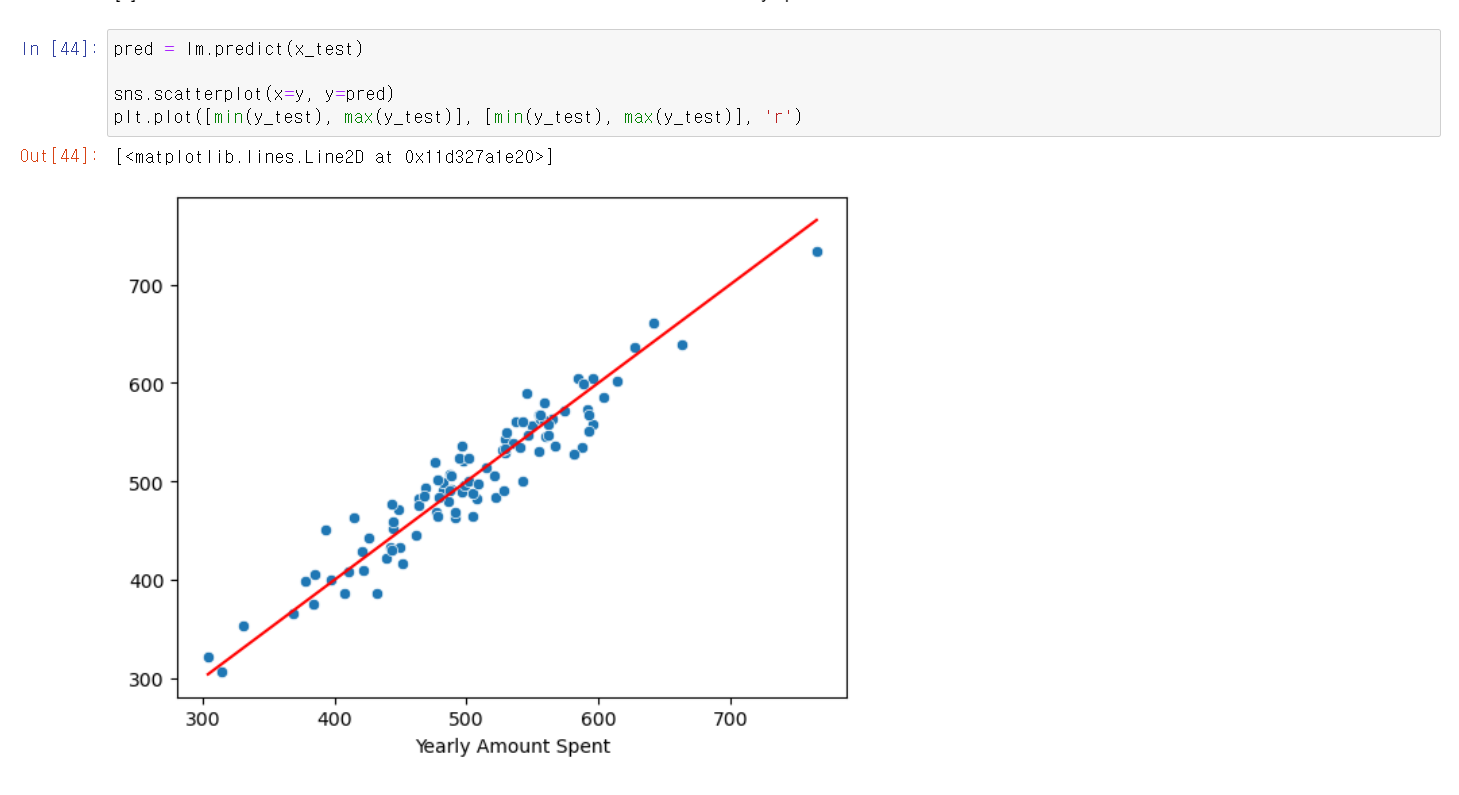
- 시각화를 통해 축에는 실제값을 값에는 예측값을 넣고 산점도 그래프를 그린 결과 시각적으로 봤을 때 나쁘지 않은 회귀분포를 보인다.
