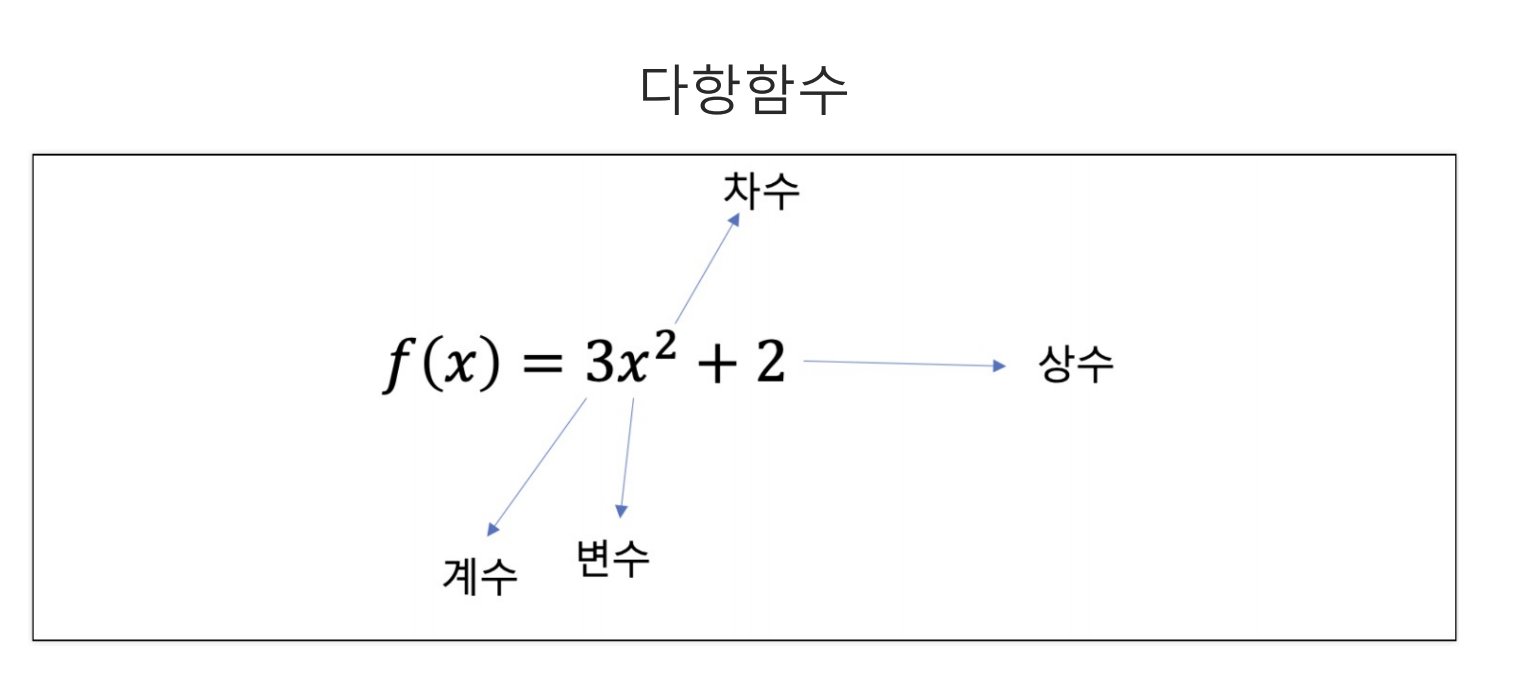
- 일반적인 다항함수는 의 모양을 가진다
: 계수이며, 이는 값이 변함을 결정짓는 기울기이기도 하다.
: 변수 위에 제곱에 따라 차수가 결정된다.
- 해당 함수를 시각화하기 위해 numpy에 임의의 숫자를 에 저장하고,
- 에는 를 저장
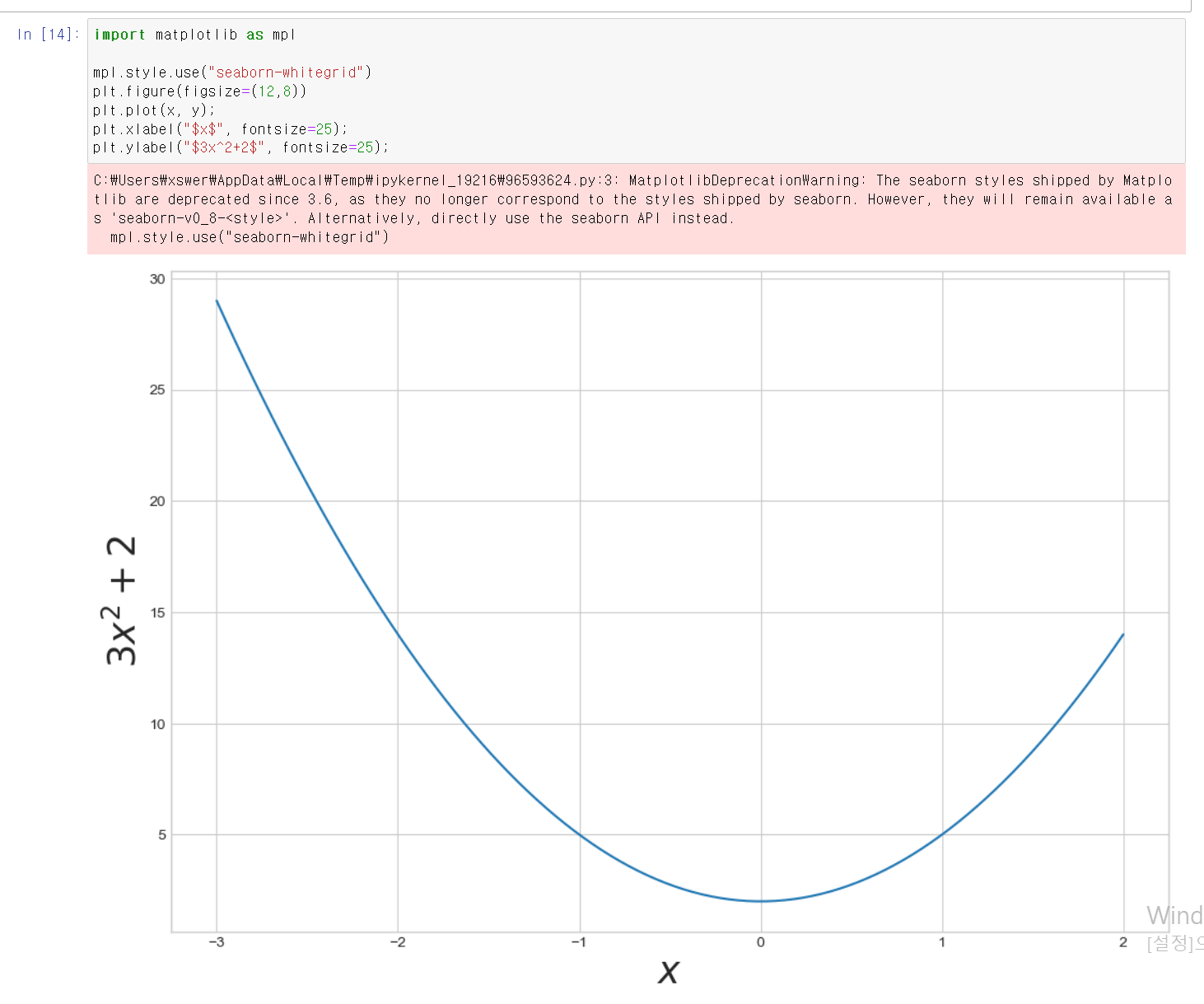
- 포물선 모양을 뒤집은 밥그릇은 같은 모양의 2차함수 그래프가 그려졌다
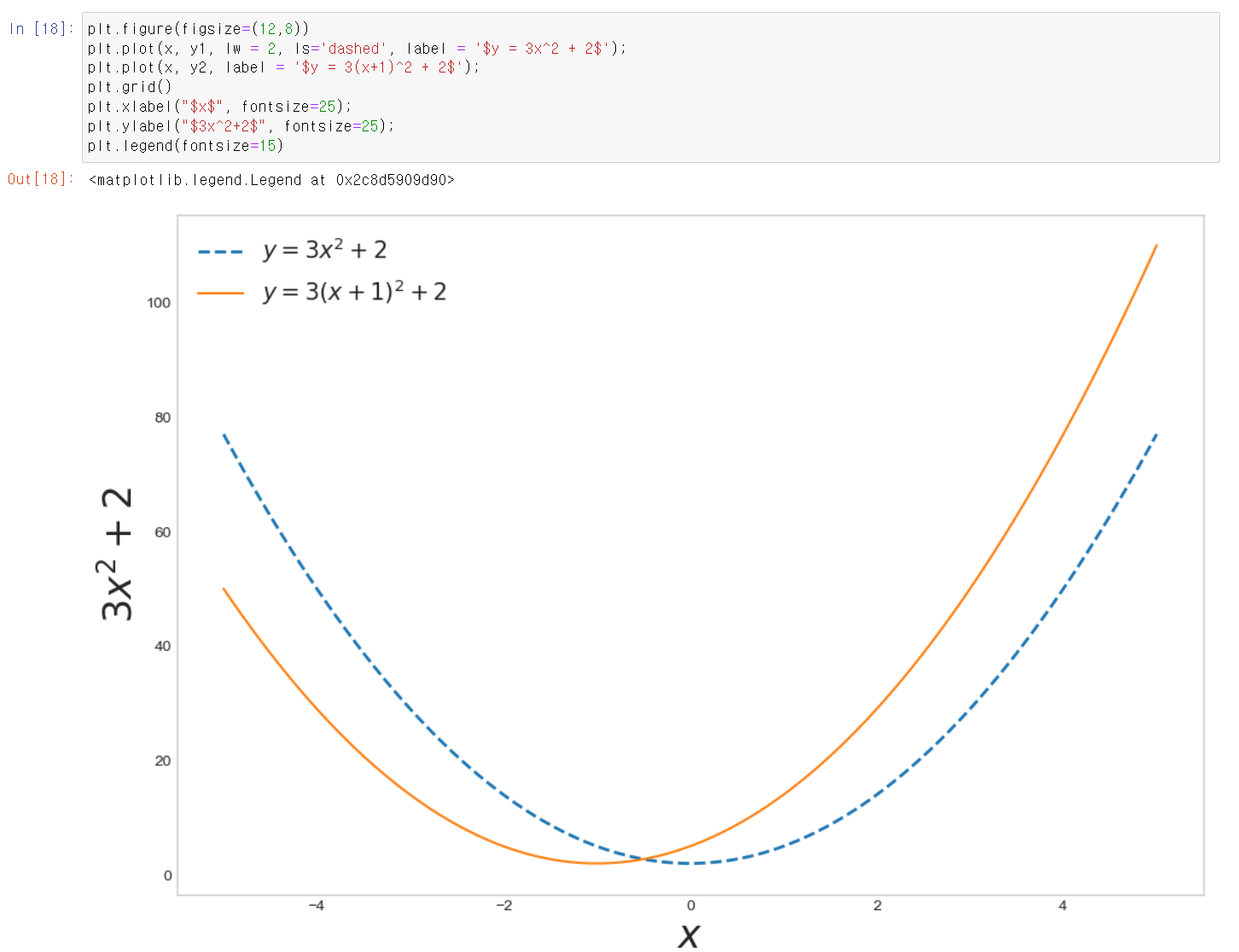
- 를 로 바꿀 경우 그래프가 기존 모양 그대로 왼쪽으로 1만큼 움직인다.
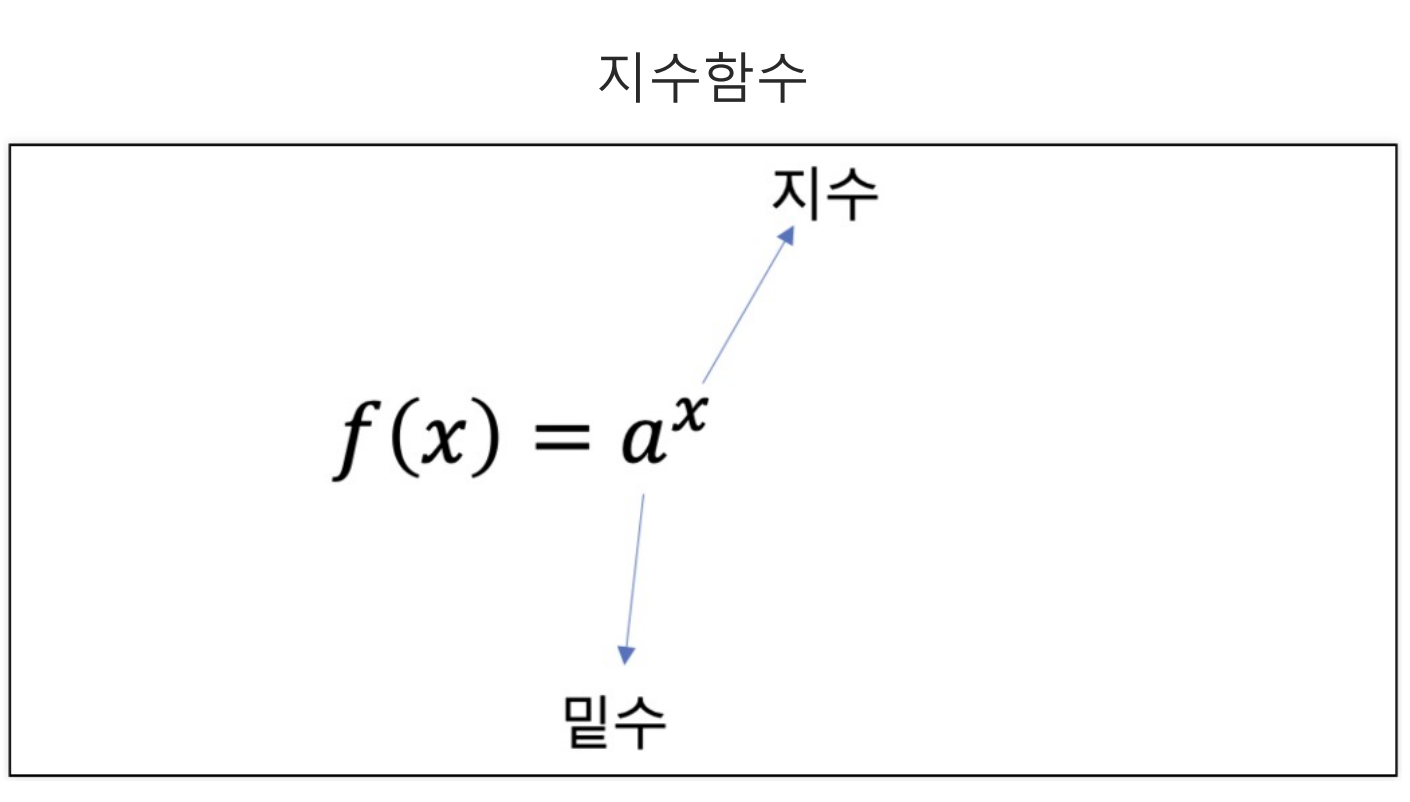
- 다음은 지수함수이다.
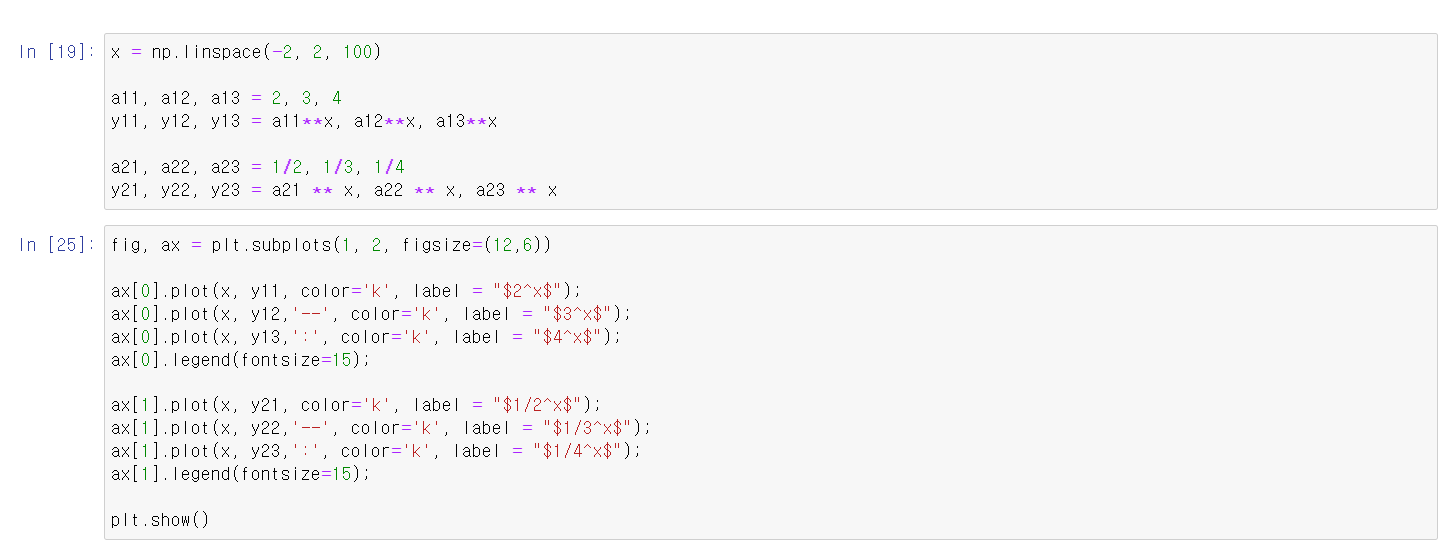
- 지수함수를 시각화하기 위해 먼저 각 변수에 값을 저장한다.
- 기존 지수함수에 분모값으로 바꿀 경우 좌우대칭된다고 생각하면 편하다.
- 지수값에 음수가 들어갈 경우 로 바뀐다.
- 는 매우 특이한 지수식의 하나인데,
- 숫자가 아무리 높아도 일정한 값에 수렴한다.
- 이것이 자연상수 의 탄생이다.
- 이는 의 값을 극한으로 올려도 결국 하나의 값에 수렴한다는 것을 의미한다.
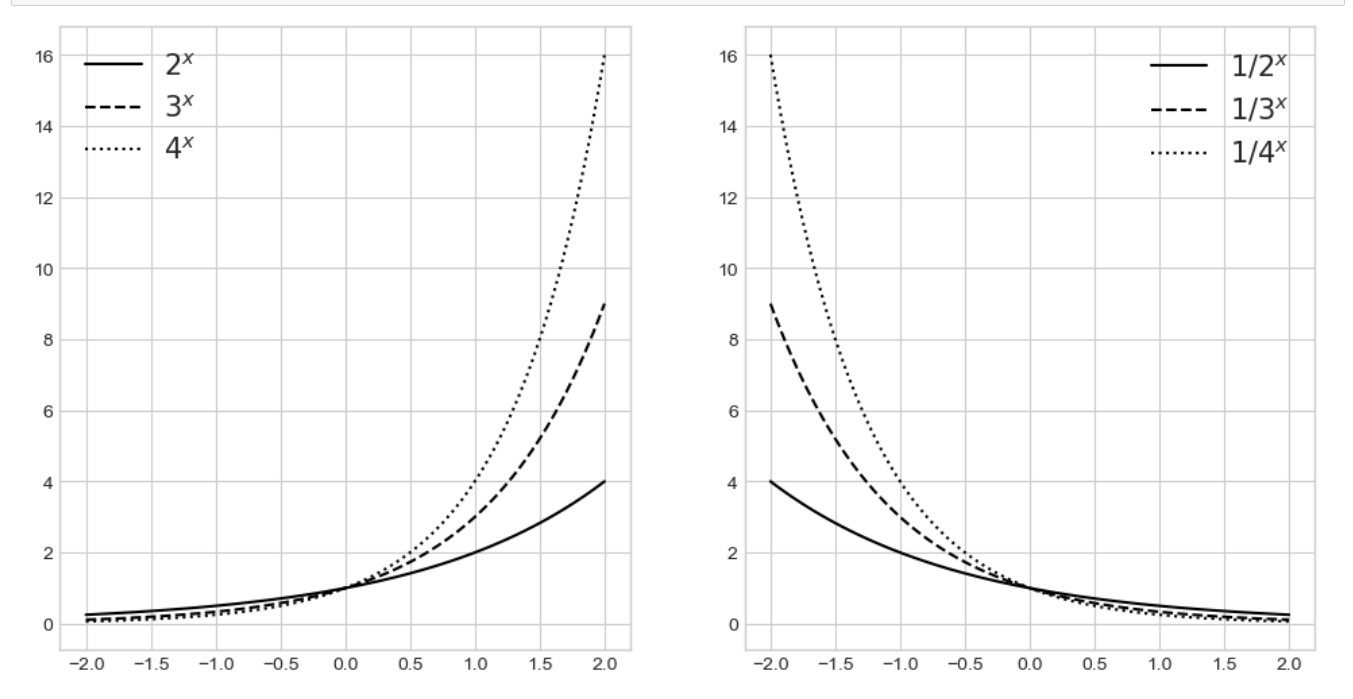
- 다음은 로그함수이다.
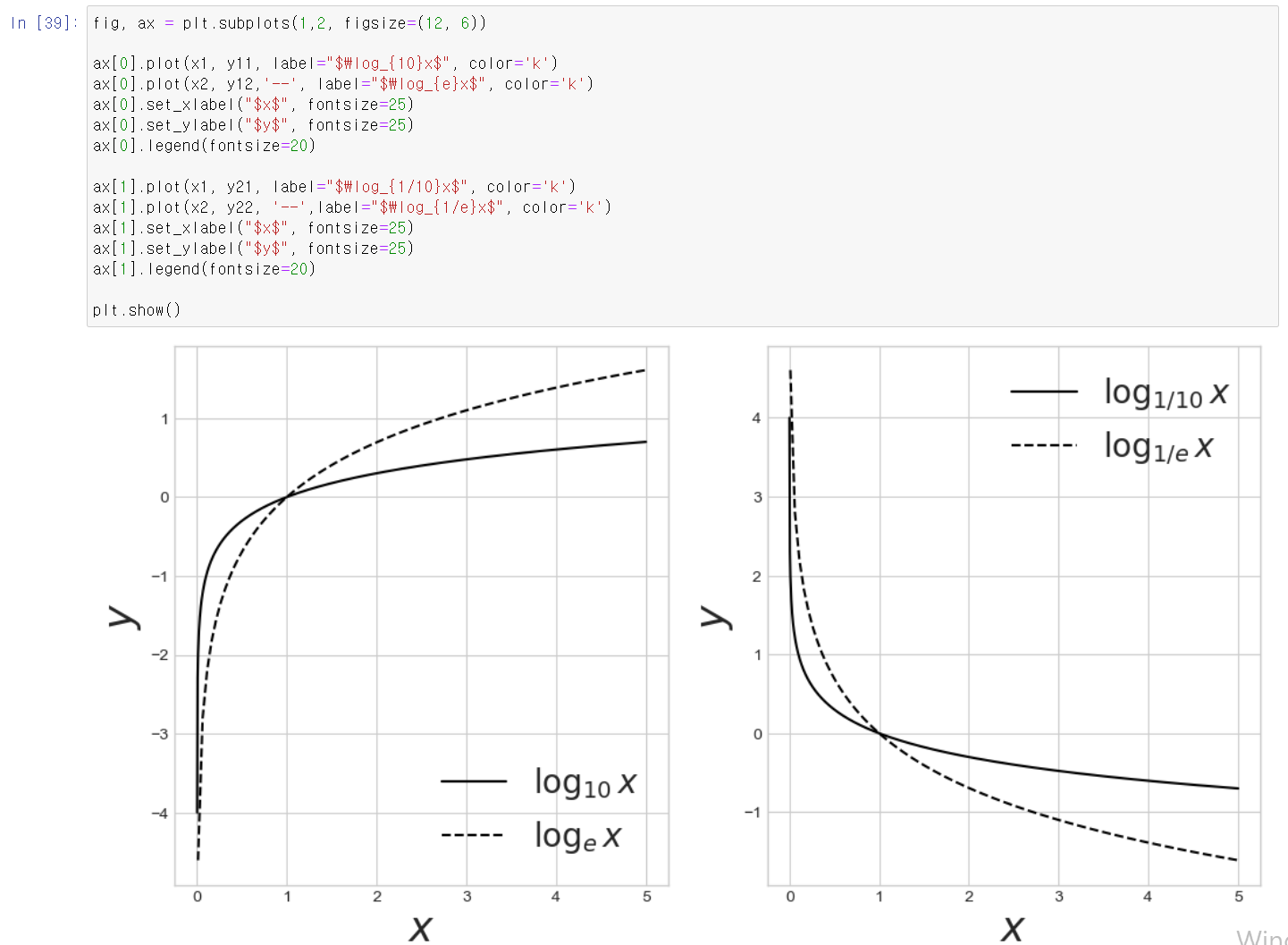
- 뭐 이렇게 생겼구나하고 넘어가면 될 것 같다.
- 다음은 시그모이드이다.
- 이는 어떠한 값을 넣어도 결과값이 0~1사이에서 나오는데, 이는 logisctic Regression 모델링에서 중요한 역할을 한다.
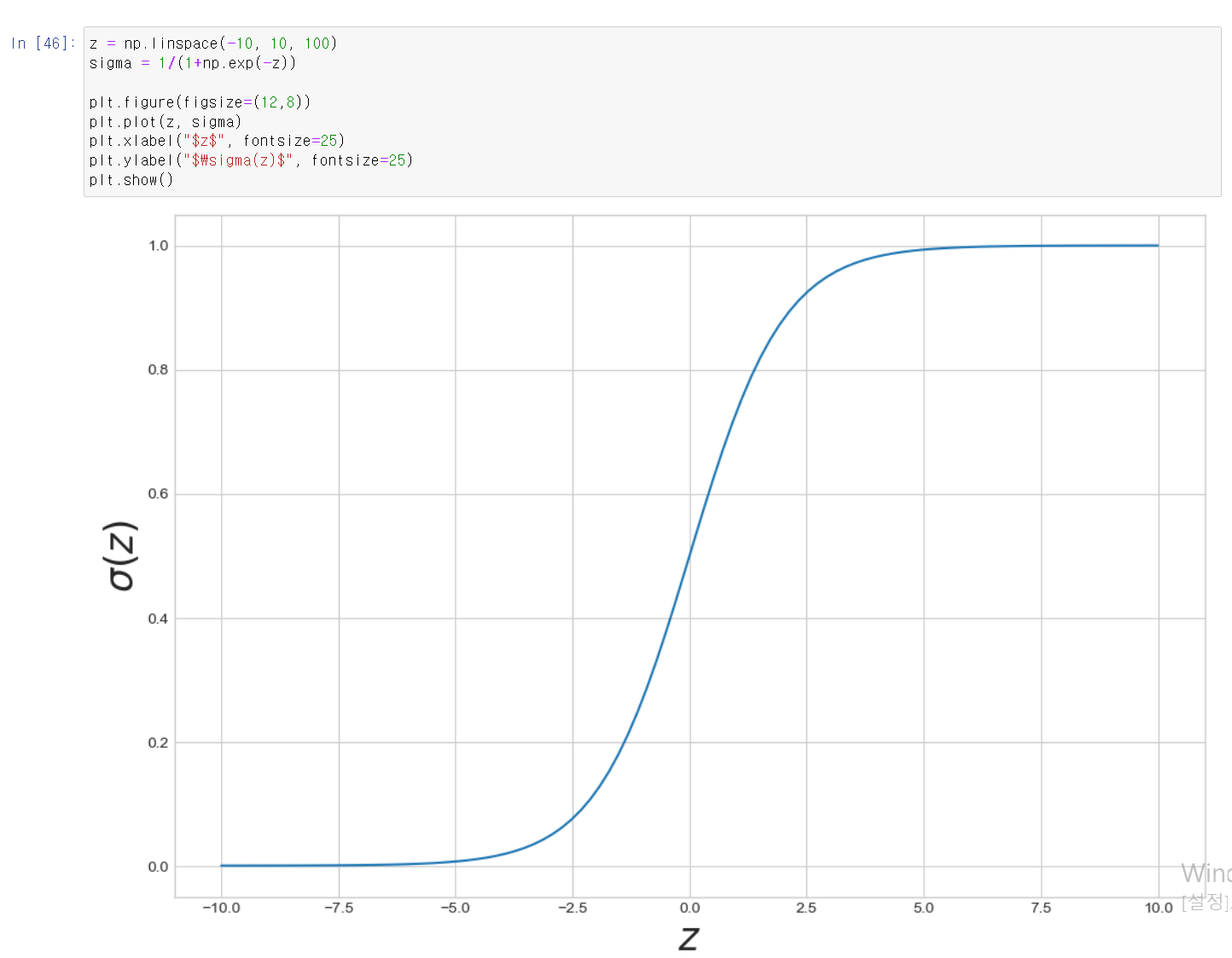
- 에 값이 변해도 결국 출력값은 0~1사이에서 나타난다.
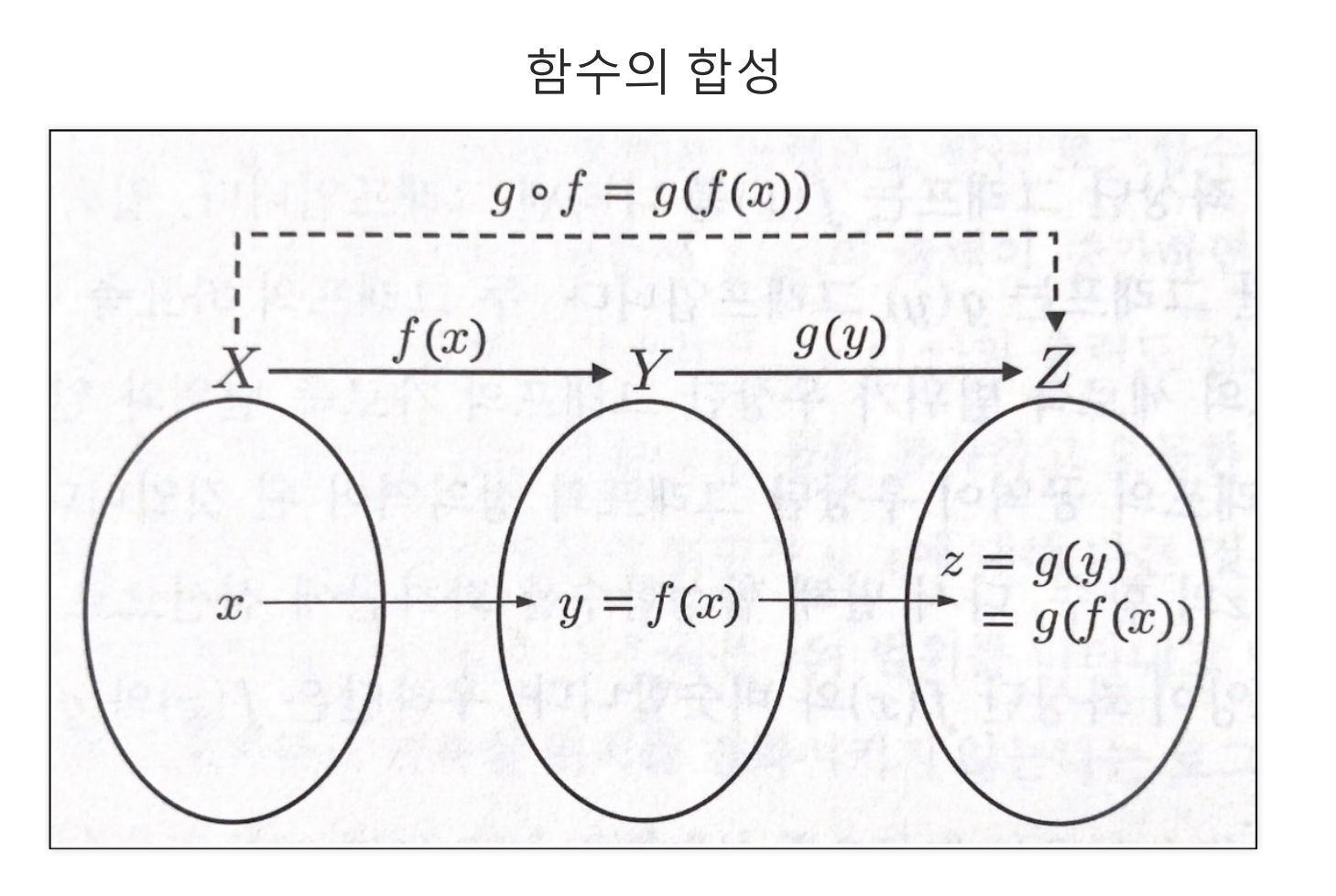
- 합성함수는 함수 안에 함수라고 생각하면 될 것 같다.
- 값이 들어가고 그에 따른 값이 다시 에 들어가서 출력된다.
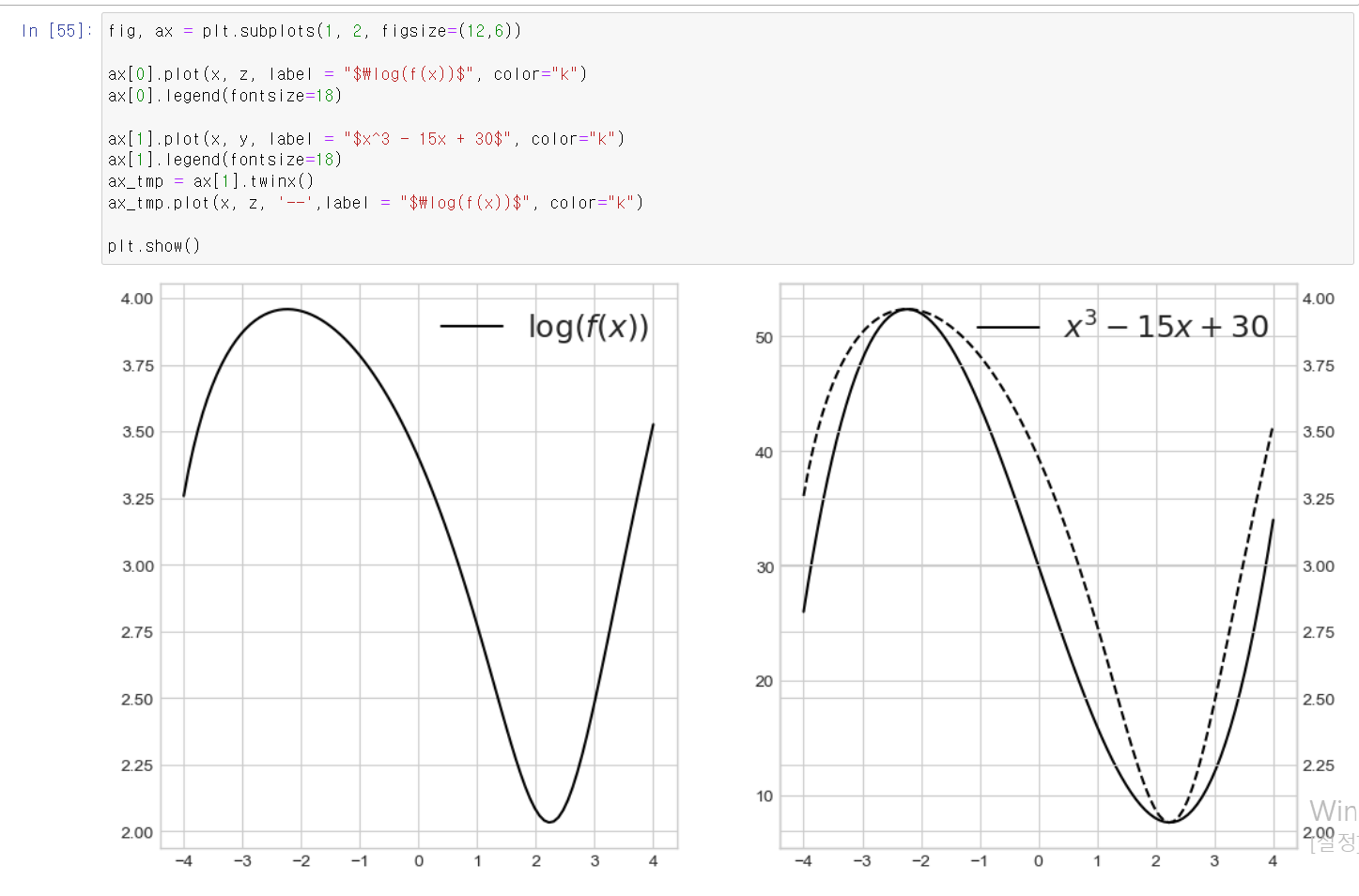
- 임의적 값과 함수식을 넣은 합성함수의 시각화 그래프는 이렇게 생겼다.
상황을 바꿀 수 없다면, 나를 바꾸자