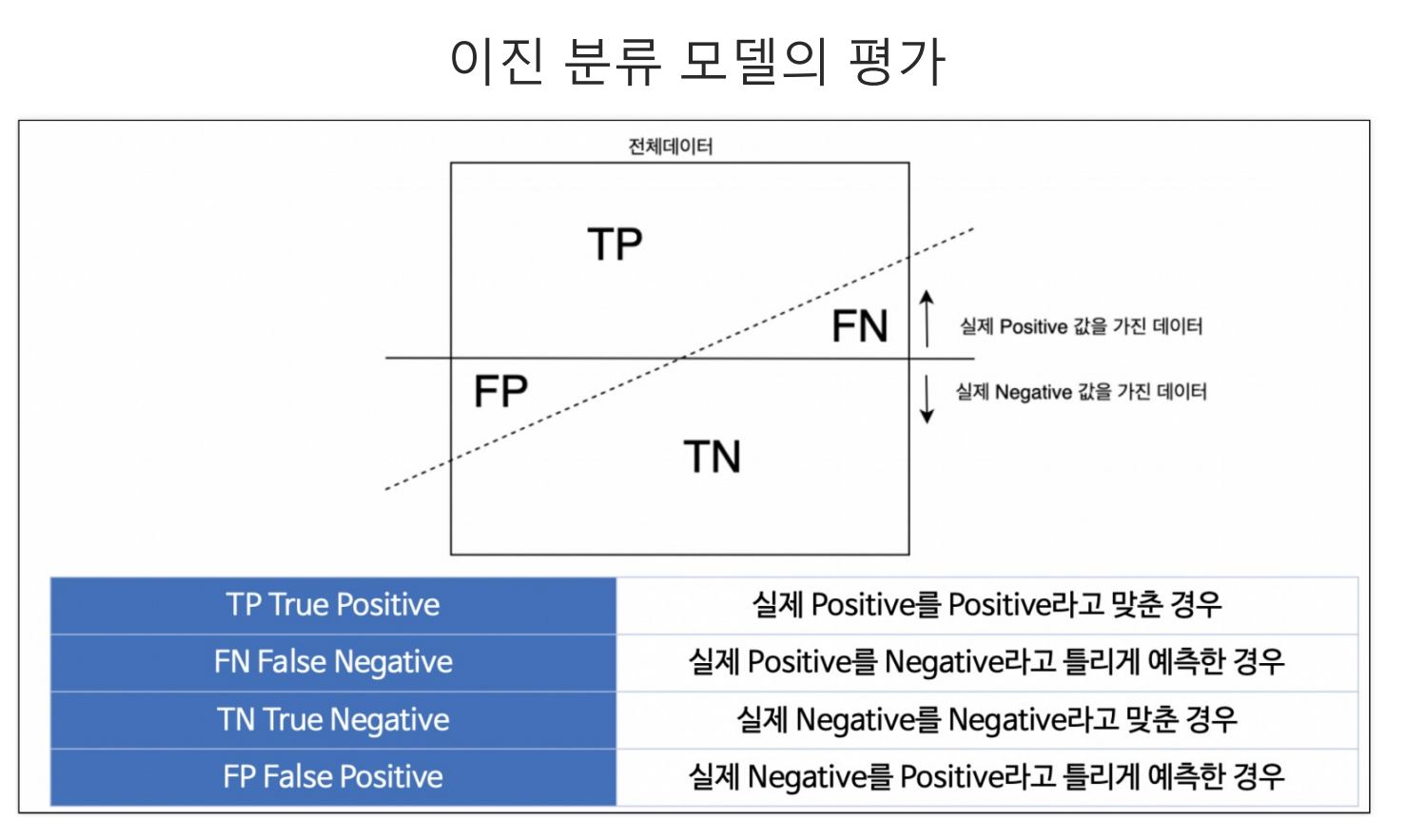
- 머신러닝에 새로운 input Data를 넣고 기존의 데이터로 만든 모델링을 통해 새로운 데이터를 예측하는 과정에서 4가지 영역으로 구분된다.
- TP(True Positive) : 실제 참값을 맞힌 경우
- FP(False Positive) : 실제 거짓 값을 참이라고 틀린 경우
- FN(False Negative) : 실제 참 값을 거짓이라고 틀린 경우
- TN(True Negative) : 실제 거짓 값을 거짓이라고 맞힌 경우
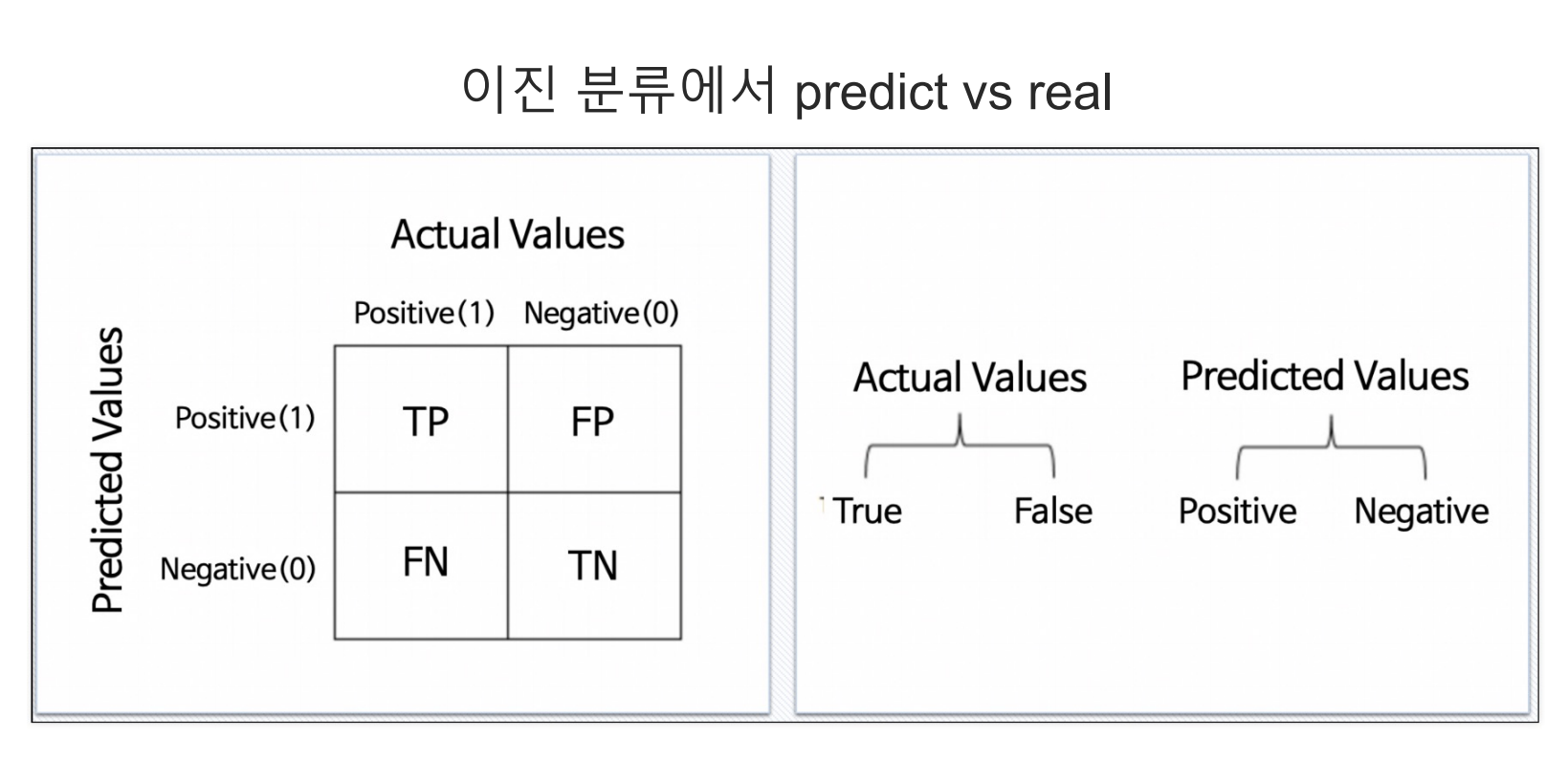
- 그림으로 보면 위와 같이 표현할 수 있다.
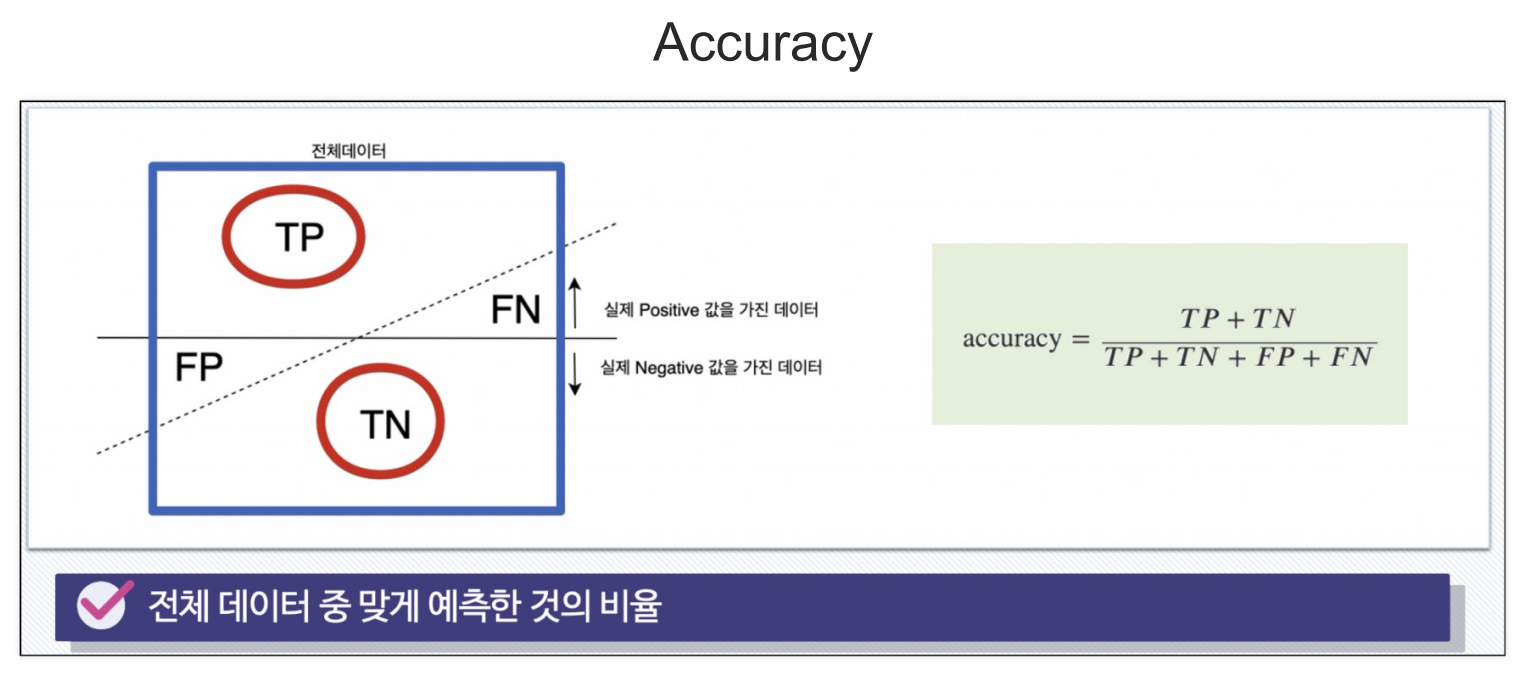
- 모델의 성능은 4가지 영역의 값을 모두 더한 값을 분모로, 맞힌 값을 분자로 넣을 수 있다.
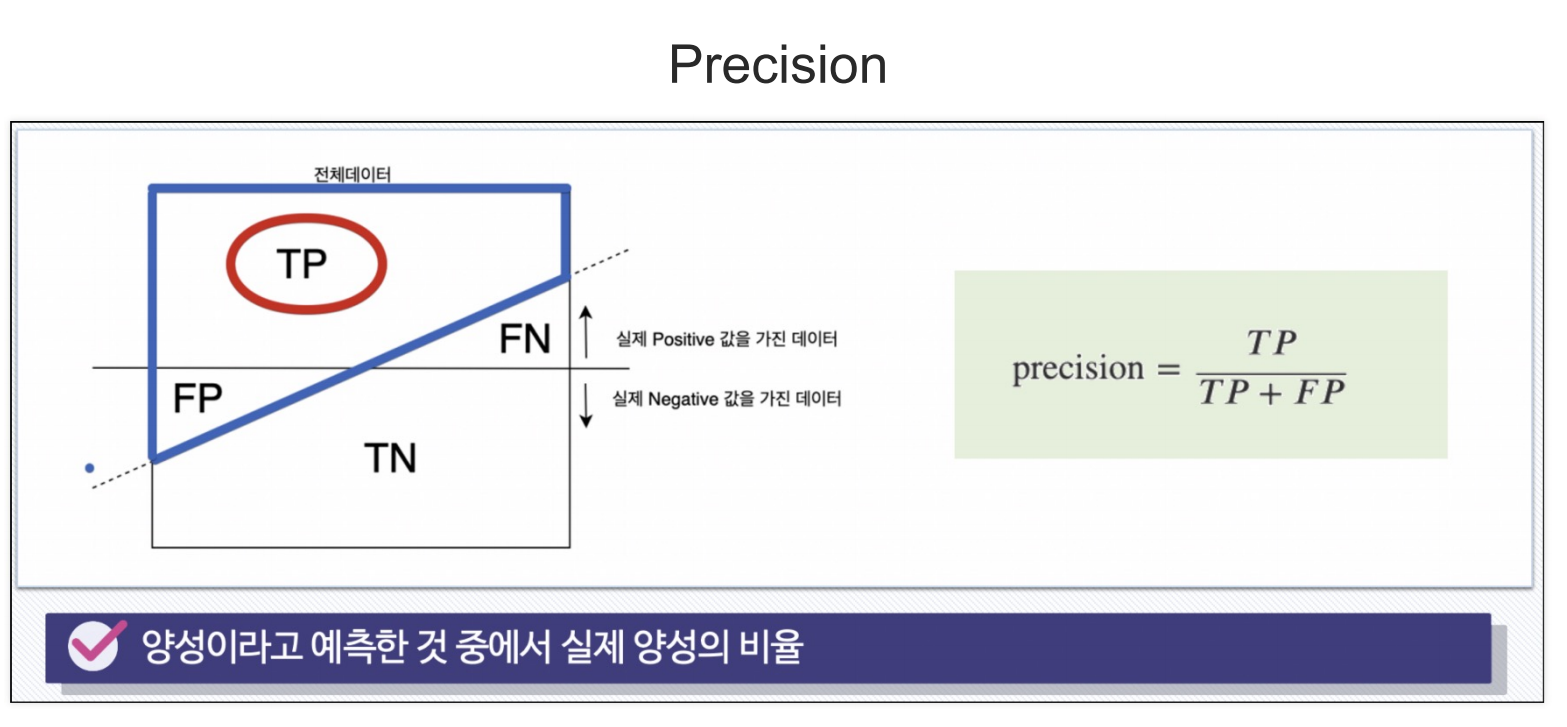
- 모델이 참이라고 예측한 값 중에 실제 참값의 비율

- 모든 참값 중 실제로 참값이라고 맞힌 비율
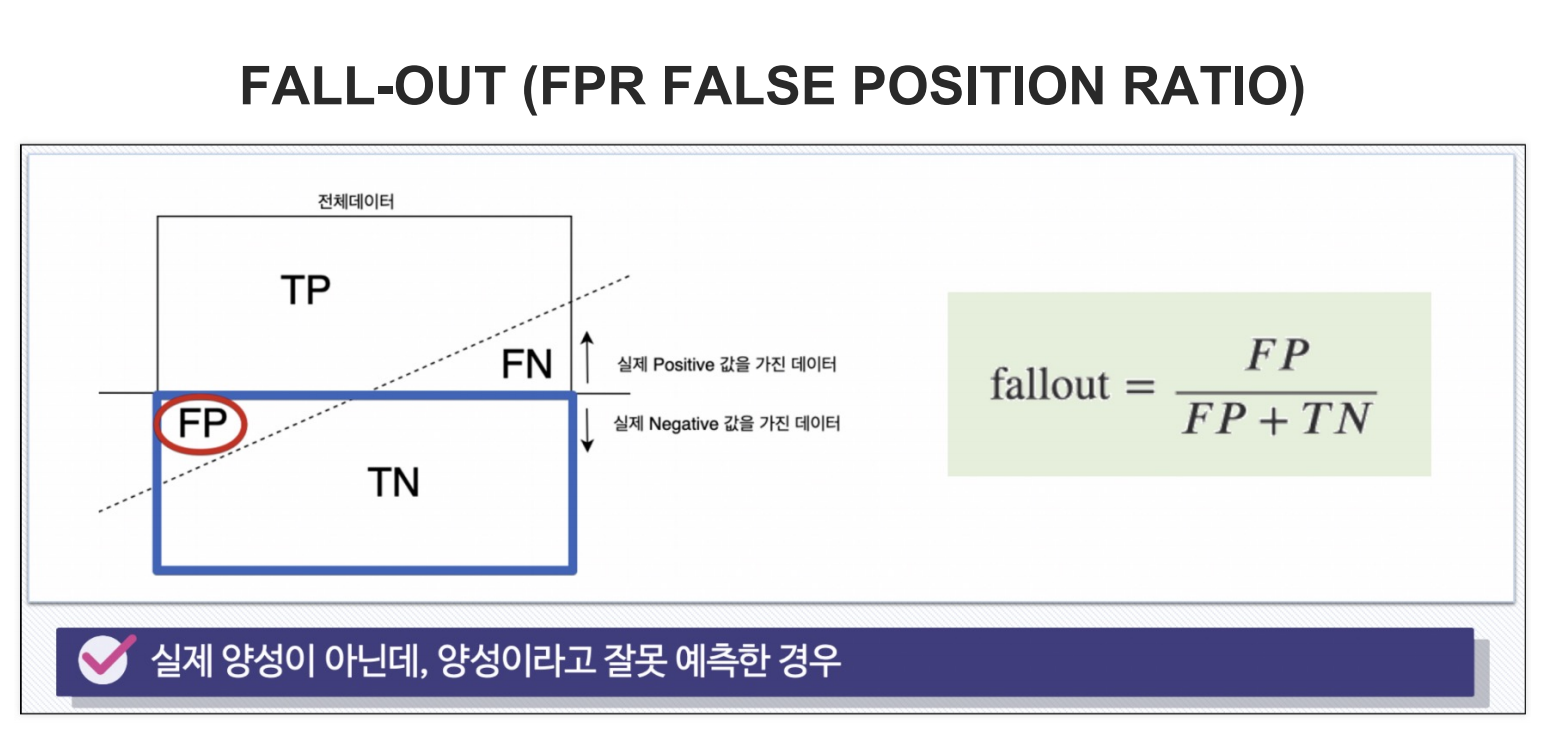
- 실제 거짓값 중 거짓값이라고 맞힌 비율
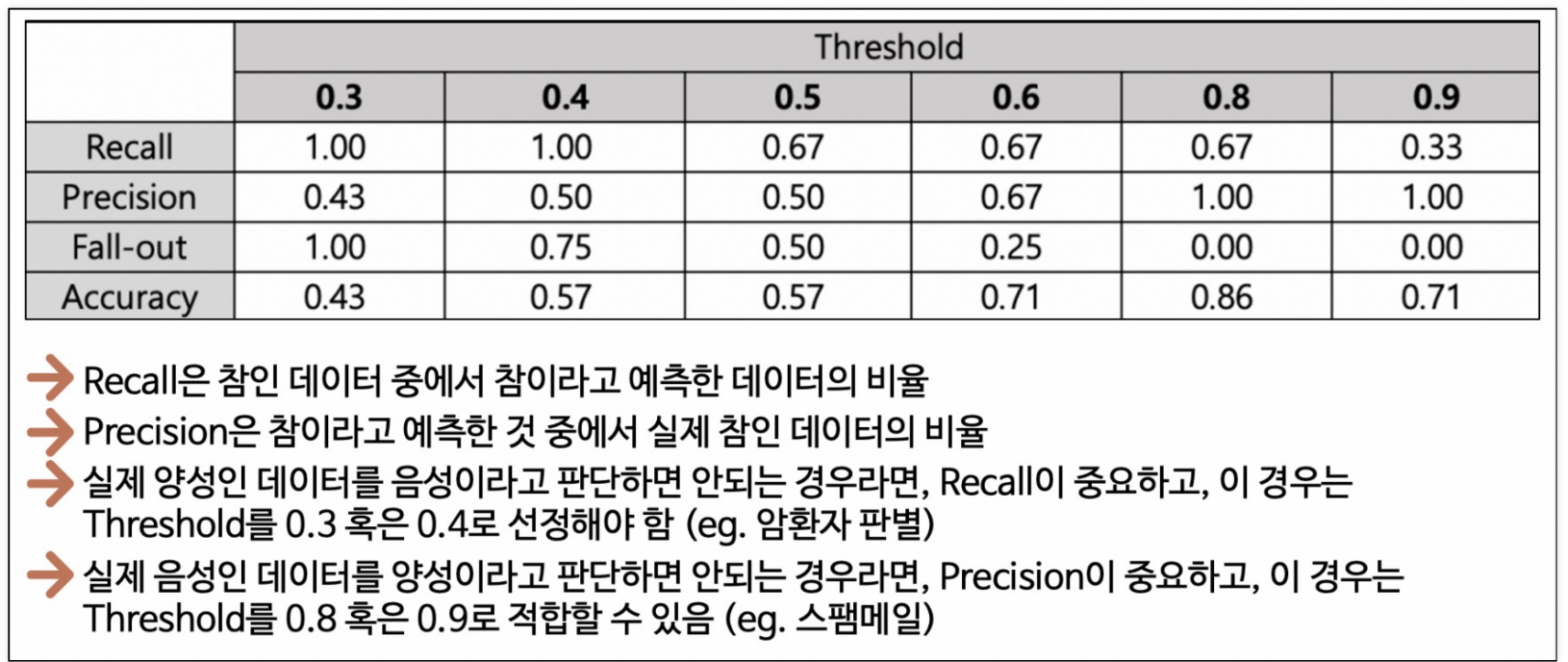
- Threshold는 참값과 거짓값을 나누는 구분기준인데, 값을 바꿈에 따라 Racll, Precision, Fall-out, Accuracy가 바뀐다.
- Threshold를 낮추면 Recall은 높아지지만, Precision의 값은 낮아진다.
- Threshold를 높히면 Recall은 낮아지지만, precision의 값은 높아진다.
- 상황의 목적에 따라 Threshold값을 조정할 수 있다.

- 는 Recall과 Precision의 조화평균으로서 두 값이 모두 높아야 높은 수치를 보인다.
- 값에 넣은 수치에 따라 등으로 구분된다
- 수식은 아래와 같으며, 에 1를 넣을 경우
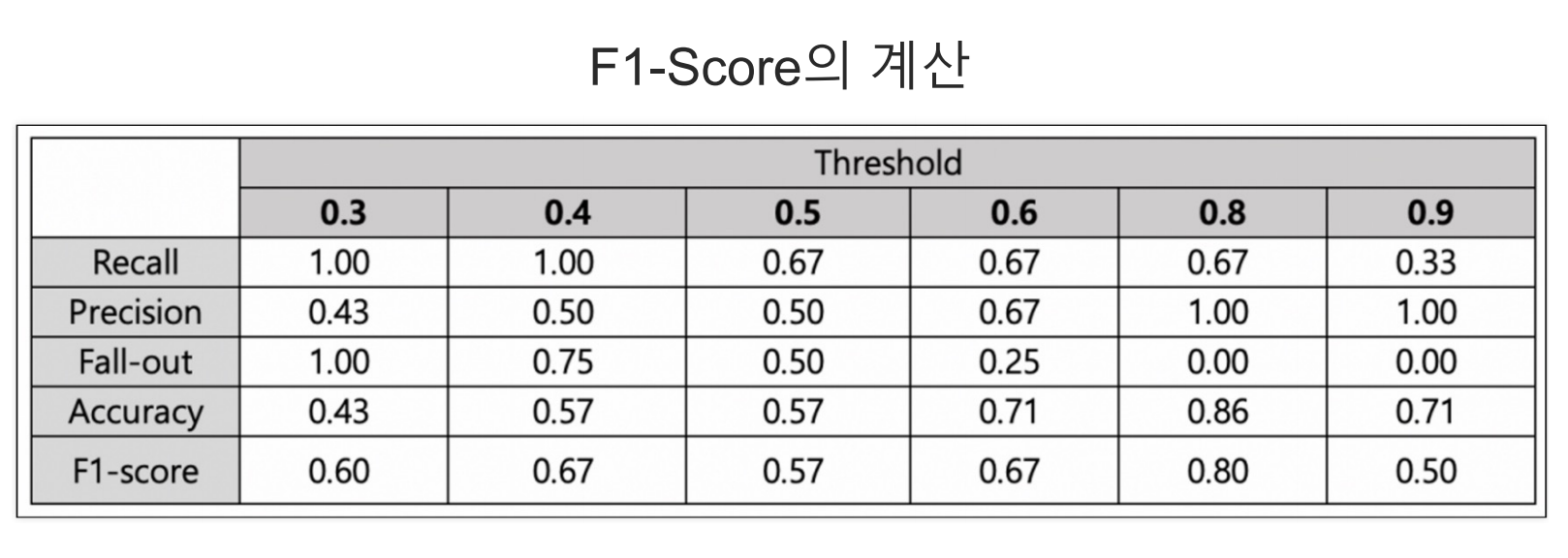
- Threshold의 값에 따라 의 값도 변한다.
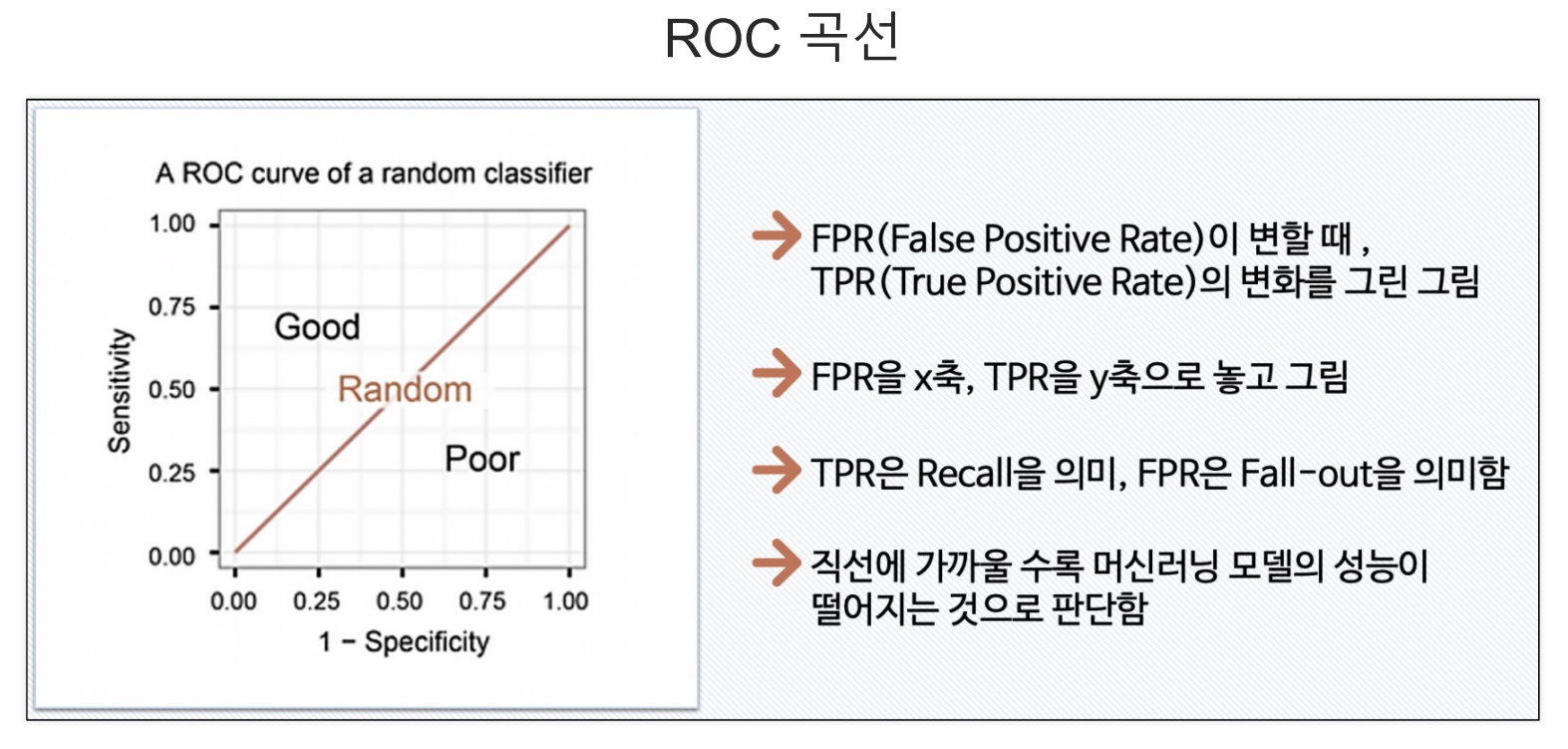
- ROC곡선은 모델의 성능을 보여주는 좋은 지표로서, 축을 FPR로 축을 TRP
- 왼쪽 상단에 직선으로 붙을수록 좋은 성능 즉 FPR이 높아짐에 따라 TPR의 수치가 더 높아지면 좋은 성능이고, 직선(AUC값이 0.5)의 경우 좋지 못한 성능이다.
TPR(Recall) : 실제 참값 전체 중 모델이 참값을 맞힌 비율
FPR(Fall-out) : 실제 거짓값 전체 중 모델이 거짓값을 맞힌 비율
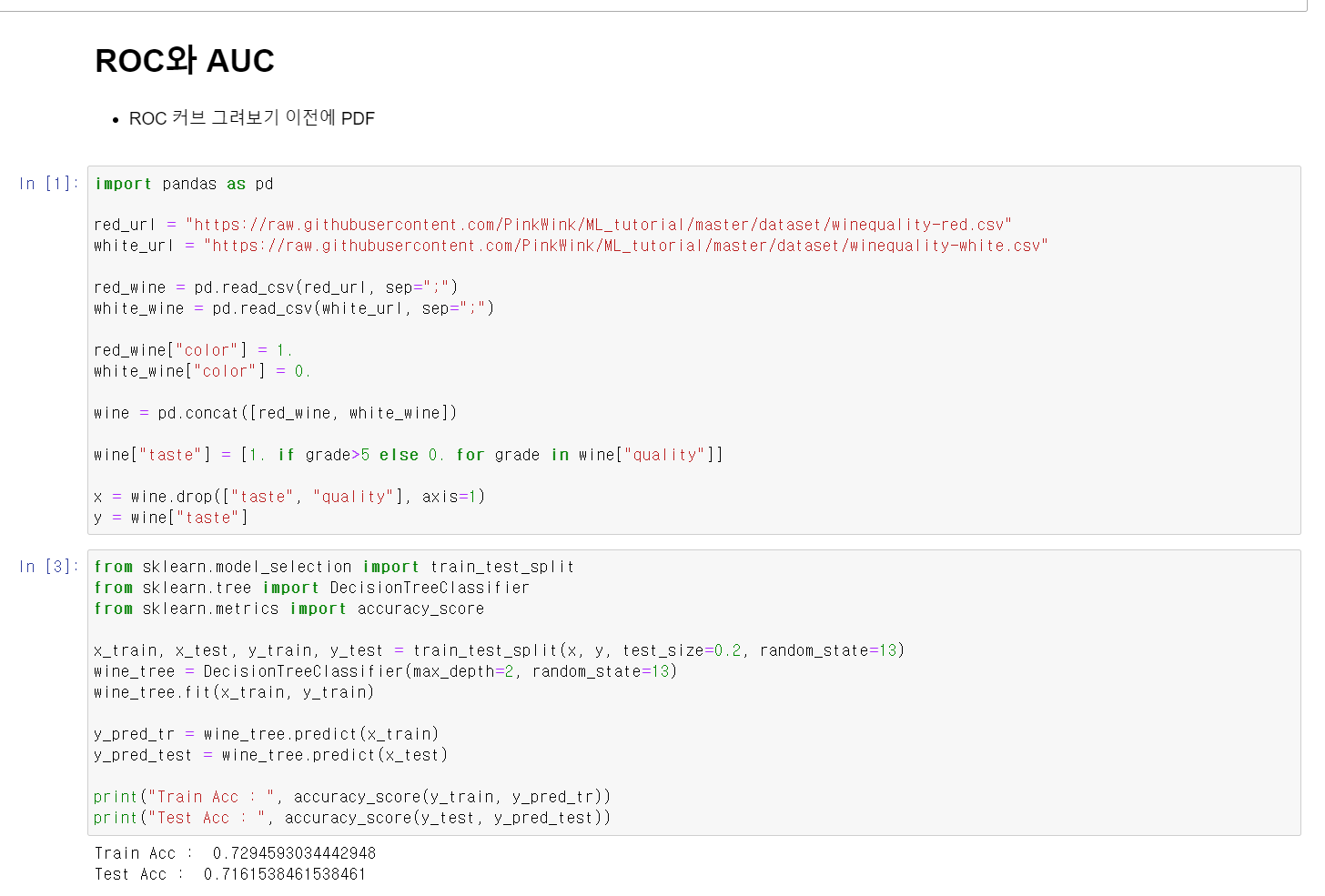
- 이제 실제 데이터에 ROC를 사용해보자
- red_wine과 white_wint값을 불러오고 이를 DecisionTreeClassifier를 통해 모델링을 하고 성능을 확인했다.
- 해당 과정은 이전 자료에 많으니...생략
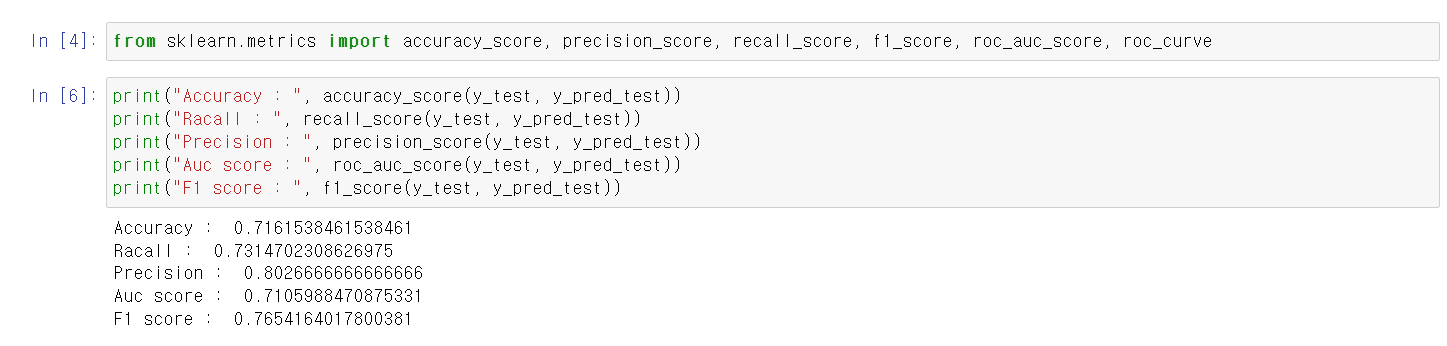
- sklearn.metrics에는 각 성능을 나타내는 값을 출력할 수 있는 많은 모듈이 있는데, 이중 accuracy_score, precision_score, recall_score, f1_score, roc_auc_score, roc_curve를 import했다.
- 실제값과 예측값을 매소드로 각각 넣고 각 수치를 print했다.
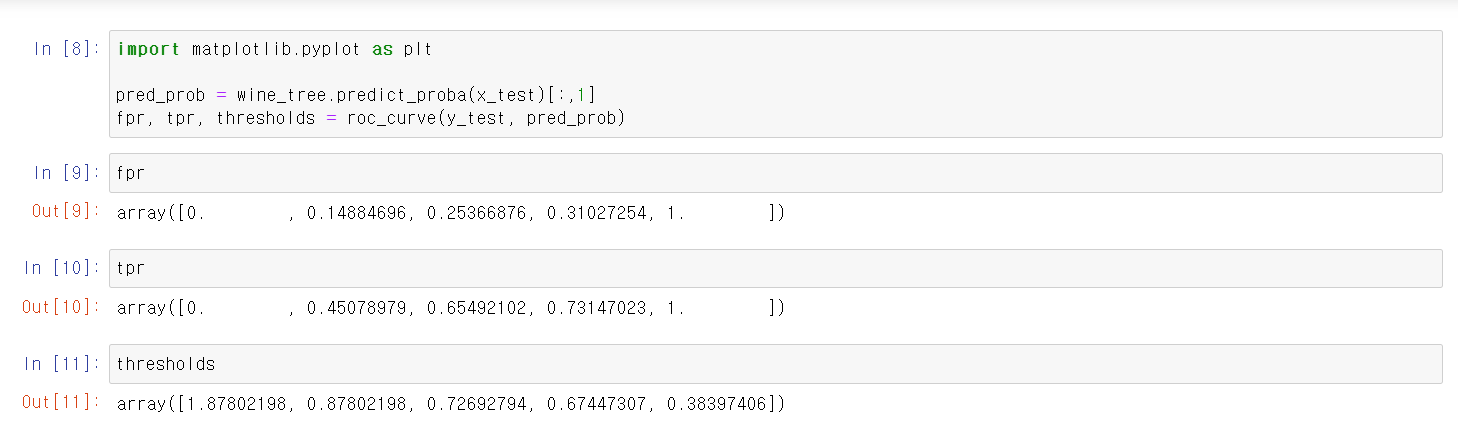
- 이제 시각화를 위해 먼저 matplotlib.pyplot를 import하고
- pred_prob 변수에 모델딩 예측값의 0이 될 확률과 1이 될 확률을 출력하는 predict_prob를 저장
- roc_curve(실제값, 예측값의 확률)를 fpr, tpr, thresholds변수에 저장
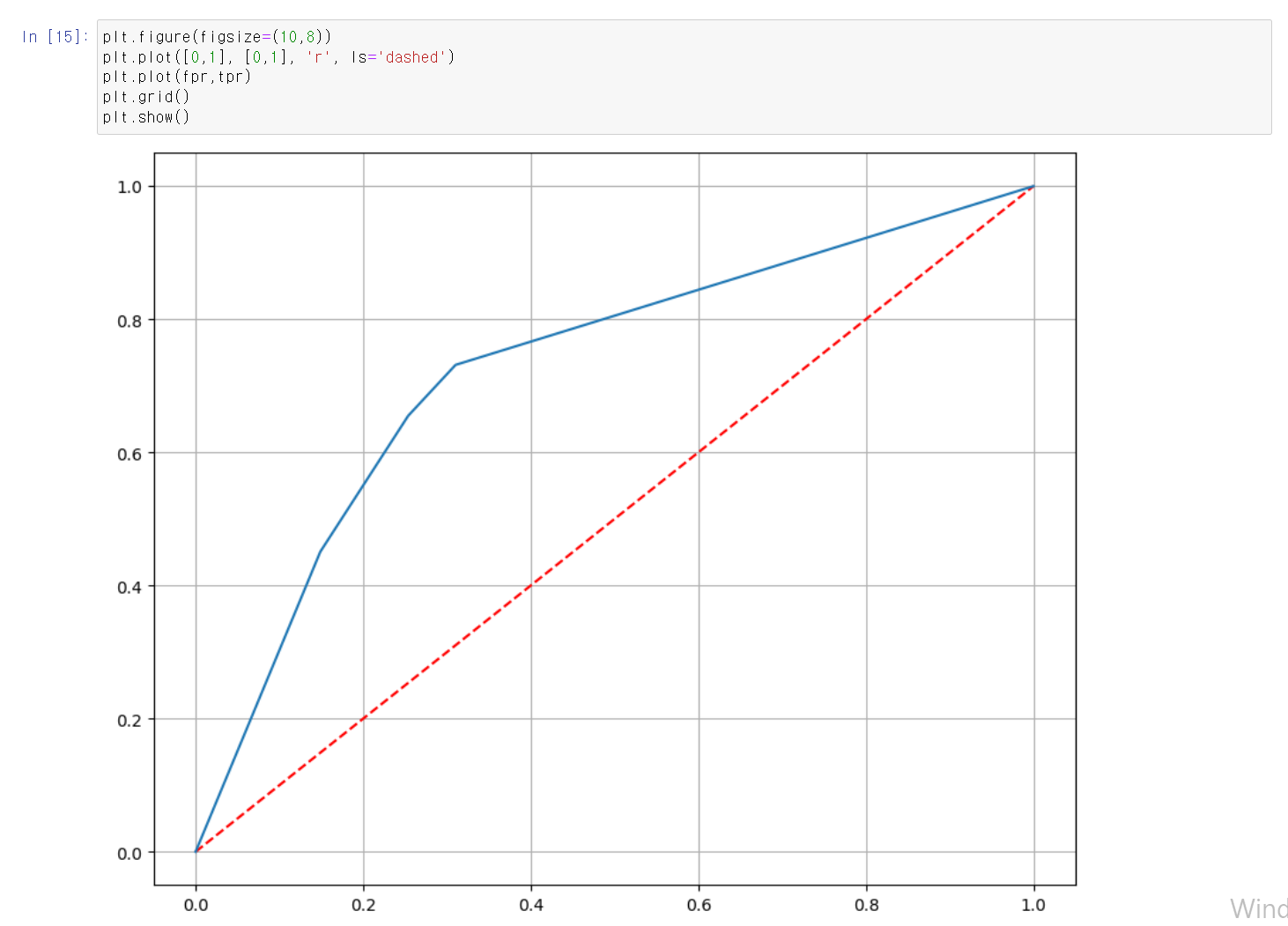
- 임의적 [0,1], [0,1] 직선을 긋고, ROC커브를 그린 결과 나름 괜찮은(괜찮은가...?) ROC커브값을 시각화했다.
