
트리 (Tree)
트리에 대하여 이어서 알아 보았다.
LeetCode 297.Serialize and Deserialize Binary Tree
이진 트리를 배열로 직렬화하고, 반대로 역직렬화하는 기능을 구현하라. 즉 다음과 같은 트리는 [1, 2, 3, null, null, 4, 5] 형태로 직렬화할 수 있을 것이다.

Solution 1 직렬화 & 역직렬화 구현
직렬화와 역직렬화를 구현하기 위해서는 이진 트리의 특징과 표현을 정확히 알아야 한다. 이진 트리는 논리적 구조이기 때문에 파일이나 디스크에 저장하기 위해서는 물리적 구조로 바꿔주어야 하고 이 과정이 직렬화이다. 역직렬화는 이 과정의 반대가 된다.
이진 트리를 직렬화하면 배열에 빈틈없이 들어가게 된다. 자식이 없는 경우에도 null을 넣게 되면 정확한 자리에 들어가게 된다. 배열에 들어가는 순서는 BFS의 순서와 같이 들어가야 직관적으로 보기 좋기 때문에 BFS로 구현할 것이다. 이렇게 될 경우 현재 노드의 부모 노드 인덱스는 현재 인덱스/2가 되고, 현재 노드의 왼쪽 자식 인덱스는 현재 인덱스*2, 오른쪽 자식 인덱스는 현재 인덱스*2+1이 된다. 이를 통해 현재 인덱스의 깊이를 알 수 있게 된다. 앞서 말한것 처럼 비어있는 위치는 null로 대체되기 때문에 모든 트리는 배열로 표현이 가능하다.
직렬화
직렬화는 앞서 말한대로 BFS를 사용하여 구현한다. 큐를 데크로 선언하여 root를 큐에 넣어주고, 큐를 순회하면서 추출값에 대한 왼쪽, 오른쪽 자식을 큐에 넣어주고, 결과 리스트 result에는 현재의 값을 넣어준다. 만약 큐에서 추출한값이 없을 경우에는 null을 의미하는 #를 넣어준다. (파이썬에서는 리스트에 null을 넣을 수가 없기 때문에 #로 대체한다.)
역직렬화
역직렬화 역시 큐를 이용해 진행한다. data를 split()을 통해 공백 기준으로 나눠진 리스트 nodes로 변환해주고, root를 TreeNode로 만든다. 이때 nodes[1]로 만들게 된다. 그리고 큐에 root를 넣어준다. nodes를 탐색해나가며 왼쪽 자식과 오른쪽 자식을 번갈아가며 채워준다. 만약 #가 나타나면 null을 의미하므로 아무런 처리를 하지 않게 된다.
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
queue=collections.deque([root])
result=['#']
while queue:
node=queue.popleft()
if node:
queue.append(node.left)
queue.append(node.right)
result.append(str(node.val))
else:
result.append('#')
return ''.join(result)
def deserialize(self, data):
if data=='# #':
return None
nodes=data.split()
root=TreeNode(int(nodes[1]))
queue=collections.deque([root])
index=2
while queue:
node=queue.popleft()
if nodes[index] is not '#':
node.left=TreeNode(int(nodes[index]))
queue.append(node.left)
index+=1
if nodes[index] is not '#':
node.right=TreeNode(int(nodes[index]))
queue.append(node.right)
index+=1
return root
# Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))LeetCode 110.Balanced Binary Tree
이진 트리가 높이 균형인지 판단하라.
높이 균형은 모든 노드의 서브 트리 간의 높이 차이가 1 이하인 것을 말한다.

Solution 1 재귀 구조로 높이 차이 계산
높이 균형은 매우 중요하다. 높이 균형이 맞아야 효율적으로 트리를 구성할 수 있고, 탐색 또한 훨씬 더 효율적으로 처리할 수 있다. 높이 균형을 매번 맞추는 AVL트리는 대표적인 자가 균형 이진 탐색 트리이다.
재귀 호출로 리프 노드까지 내려가고, 맨 마지막 노드에 이르면 각각 left=0, right=0을 반환하도록 구현했다. check()함수의 비즈니스 로직은 다음과 같다.
def check(root):
if not root:
return 0
left=check(root.left)
right=check(root.right)
if left==-1 or right==-1 or abs(left-right)>1:
return -1
return max(left, right)+1left와 right가 모두 0일 경우 차이가 1보다 크지 않으므로 max(left, right)+1로 1을 반환하게 된다. 이런식으로 1씩 증가하는 형태가 반환된다. 예제에서 false가 반환된 문제를 보면 각 리프 노드들은 1이 되고, 리프 노드들의 부모 노드들은 1씩 더 큰 값을 가지게 된다. 이 구조에서 루트의 자식인 2와 2를 비교했을 때, 왼쪽 2는 자식으로 인해 3을 가지지만, 오른쪽 2는 리프노드이기 때문에 1을 가지게 되고, 이는 1보다 큰 차이가 나게 되므로 루트가 -1을 가지게 된다.
최종 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def check(root):
if not root:
return 0
left=check(root.left)
right=check(root.right)
if left==-1 or right==-1 or abs(left-right)>1:
return -1
return max(left, right)+1
return check(root)!=-1
LeetCode 310.Minimum Height Trees
노드 개수와 무방향 그래프를 입력받아 트리가 최소 높이가 되는 루트의 목록을 리턴하라.
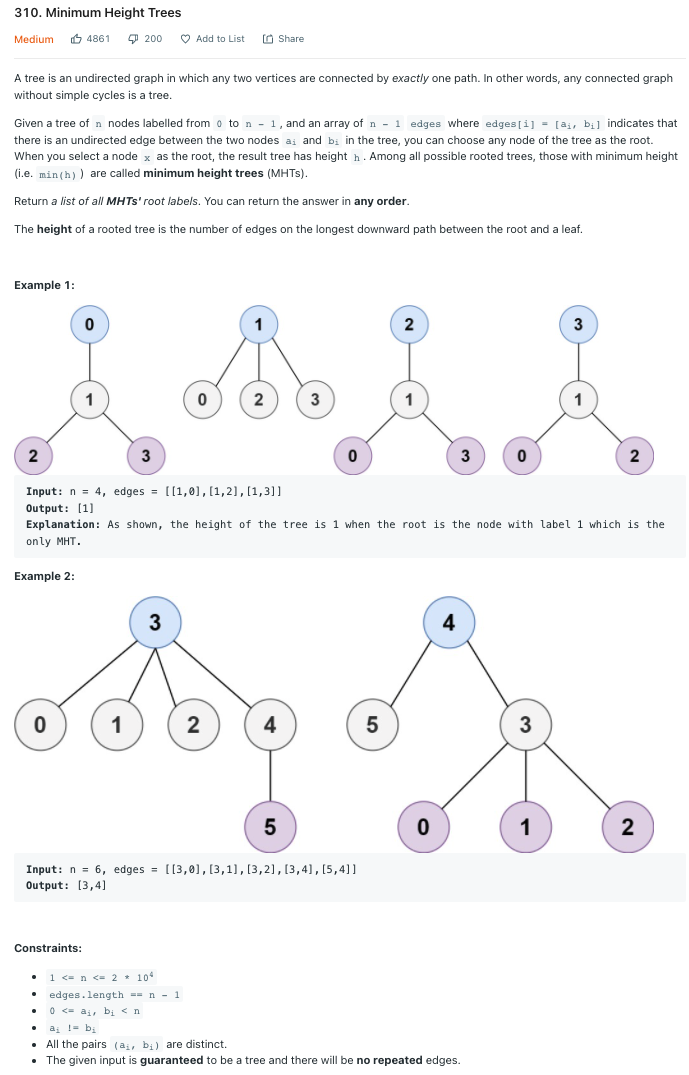
Solution 1 단계별 리프 노드 제거
최소 높이를 구성하기 위해서는 가운데 깊이에 있는 노드를 루트로 잡아야 한다. 가운데 노드를 찾기 위해서는 리프노드들을 지우는 과정을 반복하여 마지막에 남는 노드를 취해야 한다. [[1, 3], [2, 3], [3, 4], [3, 5], [4, 6], [6, 10], [5, 7], [5, 8], [8, 9]]의 트리로 문제에 접근해보면 다음과 같다.
이 트리의 경우 연결된 노드가 하나밖에 없는 리프노드 1, 2, 7, 9, 10이 제거된다.
그 다음으로는 6, 8이 제거된다.
그 다음으로는 5, 4가 제거되고 결과적으로 3만 남게 된다.
이 과정을 코드로 나타내면 트리를 인접 리스트 형태로 구현하고, 리프 노드를 찾아 leaves 리스트에 넣어준다. 그리고 다음과 같이 루트가 남을 때까지 리프를 지우는 과정을 반복한다.
while n>2:
n-=len(leaves)
new_leaves=[]
for leaf in leaves:
neighbor=graph[leaf].pop()
graph[neighbor].remove(leaf)
if len(graph[neighbor])==1:
new_leaves.append(neighbor)
leaves=new_leavesn은 전체 노드의 개수이므로 여기서 leaves, 즉 리프 노드의 개수만큼 계속 빼나가면서 최종 2개 이하가 남을 때까지 반복한다. 마지막에 남은 값이 홀수 개일 경우 루트가 최종 1개가 되지만 짝수 개일 경우에는 2개가 될 수 있다. 따라서 while 반복문은 2개까지는 계속 반복한다. 리프 노드는 반복하면서 제거한다. 그래프 딕셔너리에서 pop()으로 제거하고, 연결된 값도 찾아서 제거한다. 즉 무방향 그래프라 그래프를 각각 두 번씩 만들었기 때문에 제거도 두 번 해줘야 한다. 이때 마찬가지로 값이 1개뿐일 경우는 리프 노드라는 의미이므로 새로운 리프 노드를 new_leaves로 구성하여 교체한다. 계속 반복하면서 leaves에 최종적으로 2개 이하가 남게 되면 이 노드들이 루트가 되며 최종 결과로 반환한다. 전체 코드는 다음과 같다.
class Solution:
def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
if n<=1:
return [0]
graph=collections.defaultdict(list)
for i, j in edges:
graph[i].append(j)
graph[j].append(i)
leaves=[]
for i in range(n+1):
if len(graph[i])==1:
leaves.append(i)
while n>2:
n-=len(leaves)
new_leaves=[]
for leaf in leaves:
neighbor=graph[leaf].pop()
graph[neighbor].remove(leaf)
if len(graph[neighbor])==1:
new_leaves.append(neighbor)
leaves=new_leaves
return leaves
이진 탐색 트리(BST)
이진 트리는 정렬의 여부에 관계 없이 모든 노드가 둘 이하의 자식 노드를 가지는 트리를 말한다. 이진 탐색 트리는 정렬된 트리를 의미하는데, 노드의 왼쪽 서브 트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이뤄져 있는 반면, 노드의 오른쪽 서브 트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이뤄져 있는 트리를 의미한다. 이렇게 왼쪽과 오른쪽의 값들이 각각 값의 크기에 따라 정렬되어 있는 트리를 이진 탐색 트리라고 한다. 이 트리의 가장 큰 장점은 탐색 시간이 O(log n)이라는 것이다.
탐색 시간이 O(log n) 밖에 걸리지 않는 이유는 찾고자 하는 노드의 값과 현재 노드의 값을 비교하며 현재 노드가 찾고자 하는 값보다 크다면 왼쪽으로, 현재 노드가 찾고자 하는 값보다 작으면 오른쪽으로 이동하며 금방 찾을 수 있기 때문이다. 만약 없는 값을 찾고자 하면 범위를 좁혀 나간 뒤에 정답이 없음을 알리게 될 것이다.
그러나 이진 탐색 트리는 트리의 불균형이 있을 때 시간 복잡도가 O(log n)에서 O(n)에 근접한 시간으로 늘어나게 된다. 이럴 경우 연결 리스트와 다르지 않게 된다. 따라서 이진 탐색 트리의 균형을 맞춰줄 필요가 있다.
자가 균형 이진 탐색 트리
자가 균형(또는 높이 균형) 이진 탐색 트리는 삽입, 삭제 시 자동으로 높이를 작게 유지하는 노드 기반의 이진 탐색 트리이다.
자가 균형 이진 탐색 트리는 최악의 경우에도 이진 트리의 균형이 잘 맞도록 유지한다. 즉 높이를 가능한 한 낮게 유지하는 것이 중요하다는 의미이다. 최악의 이진 탐색 트리의 경우 마지막 노드를 찾기 위해 n번 찾아가야 하지만 균형이 잡힌 경우에는 훨씬 적은 시도 안에 찾을 수 있다.
불균형할 경우 100만 개의 노드가 있을 때, 마지막 아이템을 찾기 위해 100만 번의 연산이 필요하게 된다. 그러나 균형이 잡혀있다면 최대 19번 안에 어떤 값이든 반드시 찾아내는 것이 가능하다.
이처럼 불균형과 균형의 성능 차이는 꽤 크다. 따라서 트리의 균형, 즉, 높이의 균형을 맞추는 작업은 매우 중요하다. 이와 같이 높이 균형을 맞춰주는 자가 균형 이진 탐색 트리의 대표적인 형태로는 AVL 트리와 레드-블랙 트리 등이 있으며 레드-블랙 트리의 경우 높은 효율성으로 인하여 실무에서도 빈번하게 사용된다. 자바의 해시맵 또한 효율적인 저장 구조를 위해 해시 테이블의 개별 체이닝 시 연결 리스트와 함께 레드-블랙 트리를 병행해 저장하는 구조로 구현되어 있다.
