
트리 (Tree)
트리에 대하여 이어서 알아 보았다.
LeetCode 108.Convert Sorted Array to Binary Search Tree
오름차순으로 정렬된 배열을 높이 균형 이진 탐색 트리로 변환하라.
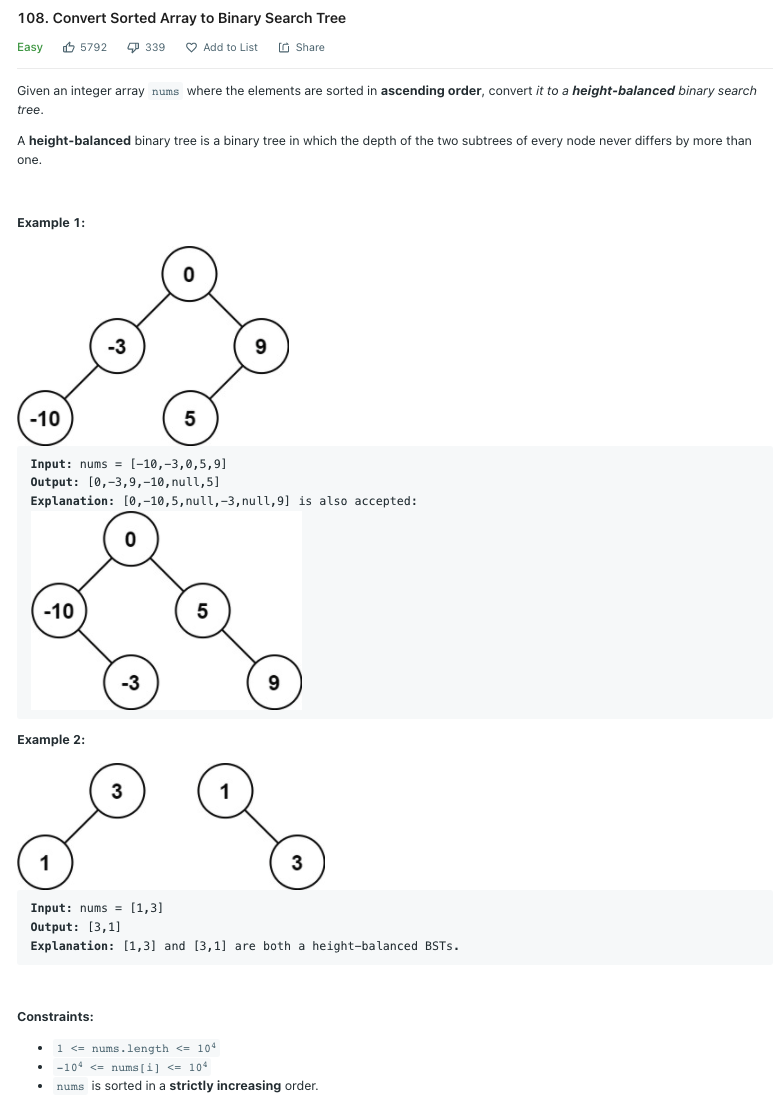
Solution 1 이진 검색 결과로 트리 구성
이 문제를 풀기 위해서는 이진 탐색 트리의 특징에 대해 정확하게 파악하고 있어야 한다. 이진 탐색 트리는 이진 검색의 마법을 적용한 이진 트리이고, 따라서 이진 탐색 트리를 만들기 위해서는 정렬된 배열을 이진 검색으로 계속 쪼개 나가기만 하면 된다. 정렬되어있지 않을 경우에는 사용할 수 없다.
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
...
mid=len(nums)//2
node=TreeNode(nums[mid])
node.left=self.sortedArrayToBST(nums[:mid])
node.right=self.sortedArrayToBST(nums[mid+1:])
...재귀 호출을 통해서 매번 가운데 값을 노드 값으로 취하도록 작성하였다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return None
mid=len(nums)//2
node=TreeNode(nums[mid])
node.left=self.sortedArrayToBST(nums[:mid])
node.right=self.sortedArrayToBST(nums[mid+1:])
return node
LeetCode 1038.Binary Search Tree to Greater Sum Tree
BST의 각 노드를 현재값보다 더 큰 값을 가진 모든 노드의 합으로 만들어라.

Solution 1 중위 순회로 노드 값 누적
자신보다 같거나 큰 값을 구하려면 자기 자신을 포함한 우측 자식 노드의 합을 구하면 된다. 앞서 BST 구조에서 설명했듯이 BST의 우측 자식 노드는 항상 부모 노드보다 큰 값이기 때문이다.
root를 입력받으면 먼저 맨 오른쪽까지 내려가고, 그 다음 부모 노드, 다시 왼쪽 노드 순으로 이동하면서 자신의 값을 포함해 누적한다. 오른쪽-부모-왼쪽 순으로 이어지며, 오른쪽 자식부터 운행하는 중위 순회에 해당됨을 알 수 있다.
def bstToGst(self, root: TreeNode) -> TreeNode:
...
self.bstToGst(root.right)
self.val+=root.val
root.val=self.val
self.bstToGst(root.left)
...self.val은 지금까지 누적된 값이고, root.val은 현재 노드의 값이다. 즉 중위 순회를 하면서 현재 노드의 값을 자기 자신을 포함한 지금까지의 누적된 값과 합한다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
val:int=0
def bstToGst(self, root: TreeNode) -> TreeNode:
if root:
self.bstToGst(root.right)
self.val+=root.val
root.val=self.val
self.bstToGst(root.left)
return root
LeetCode 938.Range Sum of BST
이진 탐색 트리(BST)가 주어졌을 때 L 이상 R 이하의 값을 지닌 노드의 합을 구하라.
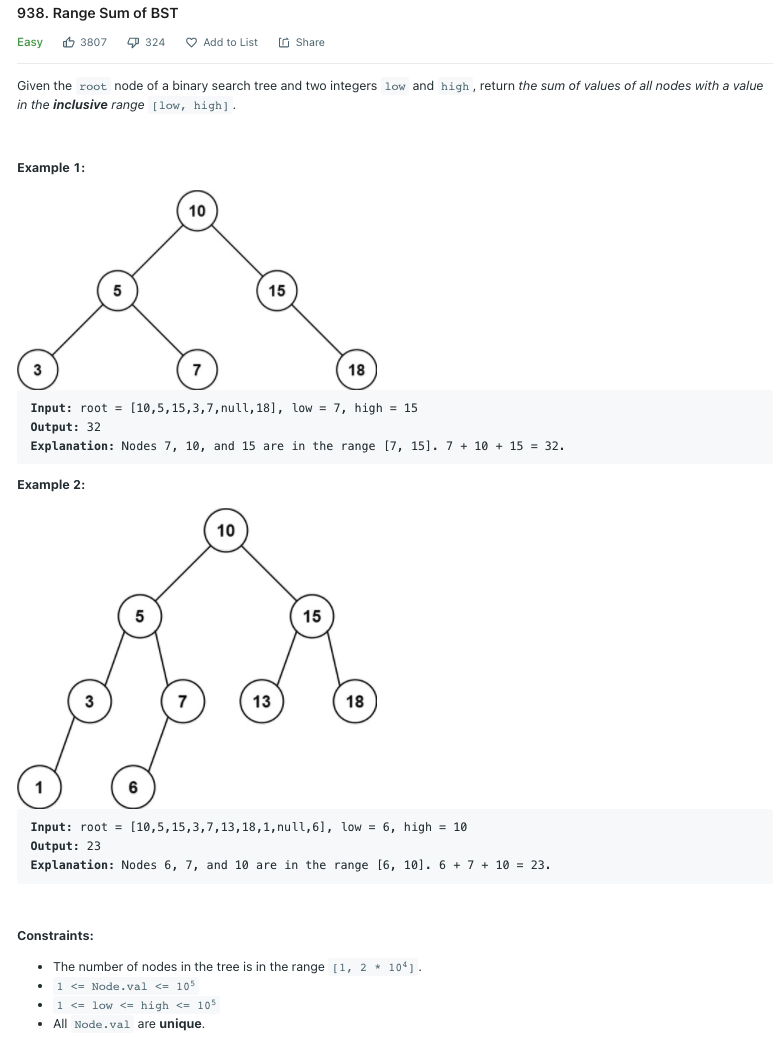
이 문제는 혼자서 먼저 풀어보았다. DFS를 통해 완전 탐색을 하며 현재 노드의 값이 범위 안에 존재할 경우 값을 누적해서 더하도록 구현하였다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
val: int=0
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
if not root:
return 0
if low<=root.val<=high:
self.val+=root.val
self.rangeSumBST(root.left, low, high)
self.rangeSumBST(root.right, low, high)
return self.val
Solution 1 재귀 구조 DFS로 브루트 포스 탐색
범위 안에 들어가는 노드들을 쉽게 찾는 방법은 DFS로 전체를 탐색한 후, 노드의 값이 범위 안에 있을 때만 값을 부여하고, 아닐 경우에는 0을 취해 계속 더해 나가면 쉽게 구할 수 있다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
if not root:
return 0
return (root.val if low<=root.val<=high else 0)+self.rangeSumBST(root.left, low, high)+self.rangeSumBST(root.right, low, high)
Solution 2 DFS 가지치기로 필요한 노드 탐색
이번에는 DFS로 불필요한 노드는 가지치기를 통해 최적화를 진행해볼 것이다. DFS로 탐색하되 범위에 해당하지 않는 가지를 쳐내는 형태로 탐색에서 배제하도록 다음과 같이 구현한다.
def dfs(node: TreeNode) -> int:
...
if node.left<low:
return dfs(node.right)
if node.right>high:
return dfs(node.left)이진 탐색 트리는 항상 왼쪽이 작고, 오른쪽이 크므로 현재 노드 root가 low보다 작을 경우, 더 이상 왼쪽으로 탐색할 필요가 없기 때문에 오른쪽만 탐색하도록 재귀 호출한다. high보다 클 경우에는 더 이상 오른쪽으로 탐색할 필요가 없기 떄문에 왼쪽으로만 탐색하도록 재귀 호출한다. 이렇게 불필요한 탐색을 줄여 최적화할 수 있다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
def dfs(node: TreeNode) -> int:
if not node:
return 0
if node.val<low:
return dfs(node.right)
elif node.val>high:
return dfs(node.left)
return node.val + dfs(node.left) + dfs(node.right)
return dfs(root)
Solution 3 반복 구조 DFS로 필요한 노드 탐색
대부분의 재귀 풀이는 반복으로 변경할 수 있다. 앞서 풀었던 재귀 풀이를 반복으로 바꿔서 풀어보았다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
stack, sum=[root], 0
while stack:
node=stack.pop()
if node:
if node.val>low:
stack.append(node.left)
if node.val<high:
stack.append(node.right)
if low<=node.val<=high:
sum+=node.val
return sum
Solution 4 반복 구조 BFS로 필요한 노드 탐색
BFS로 탐색해도 동일하다. 여기서는 스택을 단순히 큐 형태로 바꾸기만 하면 BFS를 구현할 수 있다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
q, sum=collections.deque([root]), 0
while q:
node=q.popleft()
if node:
if node.val>low:
q.append(node.left)
if node.val<high:
q.append(node.right)
if low<=node.val<=high:
sum+=node.val
return sum
LeetCode 783.Minumum Distance Between BST Nodes
두 노드 간 값의 차이가 가장 작은 노드의 값의 차이를 출력하라.
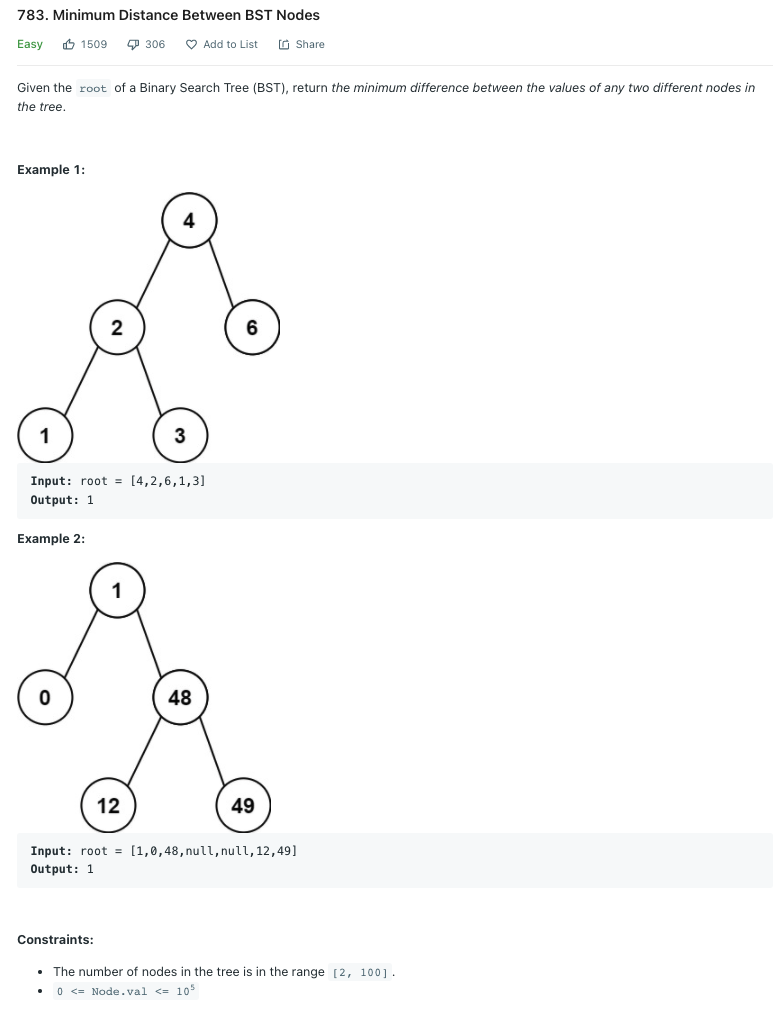
Solution 1 재귀 구조로 중위 순회
D
/ \
C G
/ \
B E
/ \ / \
A F H I이와 같은 이분 탐색 트리가 있다고 가정하고 D와 가장 값의 차이가 작을 수 있는 노드는 단 2개 있다. 그 노드들은 바로 I와 G이다.
D->B의 차이는 D->C보다 무조건 크다. 왼쪽으로 갈수록 값이 더 작아지기 때문이다. D->H는 D->E보다 무조건 크다. 이러한 반복이 이어지면 D->I가 가장 작은 값임을 알 수 있다. 물론 G가 최선의 값이 될 수도 있다.
이렇게 비교할 수 있는 탐색 순서는 어떻게 구현해야 할까? 간단하게 중위 순회를 하면서 이전 탐색 값과 현재 값을 비교하면 바로 이 순서대로 비교할 수 있다.
def f():
if root.left:
f(root.left)
result=min()
if root.right:
f(root.right)이 형태가 중위 순회의 기본 뼈대가 된다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
prev=-sys.maxsize
result=sys.maxsize
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
if root.left:
self.minDiffInBST(root.left)
self.result=min(self.result, root.val-self.prev)
self.prev=root.val
if root.right:
self.minDiffInBST(root.right)
return self.result
Solution 2 반복 구조로 중위 순회
이번에는 동일한 알고리즘을 반복 구조로 구현해본다. 반복으로 풀이하면 재귀로 풀이할 때보다 훨씬 직관적이어서 이해도 편하고 풀이 또한 쉽다. 이전 풀이인 재귀 구조와 비교 순서는 동일하며, 결과 또한 동일하다. 여기에 더한 추가 장점은 재귀일 때는 prev와 result를 클래스 멤버 변수로 선언했지만, 반복 구조에서는 한 함수 내에서 처리할 수 있기 때문에 함수 내 변수로 선언이 가능하다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
prev=-sys.maxsize
result=sys.maxsize
stack=[]
node=root
while stack or node:
while node:
stack.append(node)
node=node.left
node=stack.pop()
result=min(result, node.val-prev)
prev=node.val
node=node.right
return result
DFS 풀이이기 때문에 스택을 사용했고, 오른쪽 자식 노드를 택하기 전에 비교하는 형태로 재귀와 동일하게 중위 순회로 풀이했다. 재귀와 달리 클래스 변수를 사용하지 않아도 되므로 변수 값의 변화를 추적하기가 쉽고 좀 더 직관적이다.
트리 순회
트리 순회란 그래프 순회의 한 형태로 트리 자료구조에서 각 노드를 정확히 한 번 방문하는 과정을 말한다.
그래프 순회와 마찬가지로 트리 순회 또한 DFS 또는 BFS로 탐색하는데, 특히 이진 트리에서 DFS는 노드의 방문 순서에 따라 다음과 같이 크게 3가지 방식으로 구분된다. (L: 왼쪽 자식, R: 오른쪽 자식, N: 현재)
1. 전위 순회 (NLR)
2. 중위 순회 (LNR)
3. 후위 순회 (LRN)
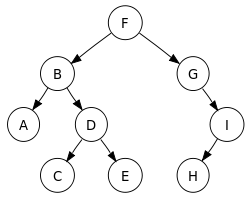
위와 같은 트리를 3가지 방식으로 순회하면 다음과 같은 순서로 나타난다.
1. 전위 순회: F->B->A->D->C->E->G->I->H
2. 중위 순회: A->B->C->D->E->F->G->H->I
3. 후위 순회: A->C->E->D->B->H->I->G->F
트리의 순회 방식은 재귀 또는 반복 모두 가능하지만 트리의 재귀적 속성으로 인해 재귀 쪽이 훨씬 더 구현이 간단하다.
전위 순회
def preorder(node):
if node is None:
return
print(node.val)
preorder(node.left)
preorder(node.right)중위 순회
def inorder(node):
if node is None:
return
inorder(node.left)
print(node.val)
inorder(node.right)후위 순회
def postorder(node):
if node is None:
return
postorder(node.left)
postorder(node.right)
print(node.val)LeetCode 105.Construct Binary Tree from Preorder and Inorder Traversal
트리의 전위, 중위 순회 결과를 입력값으로 받아 이진 트리를 구축하라.
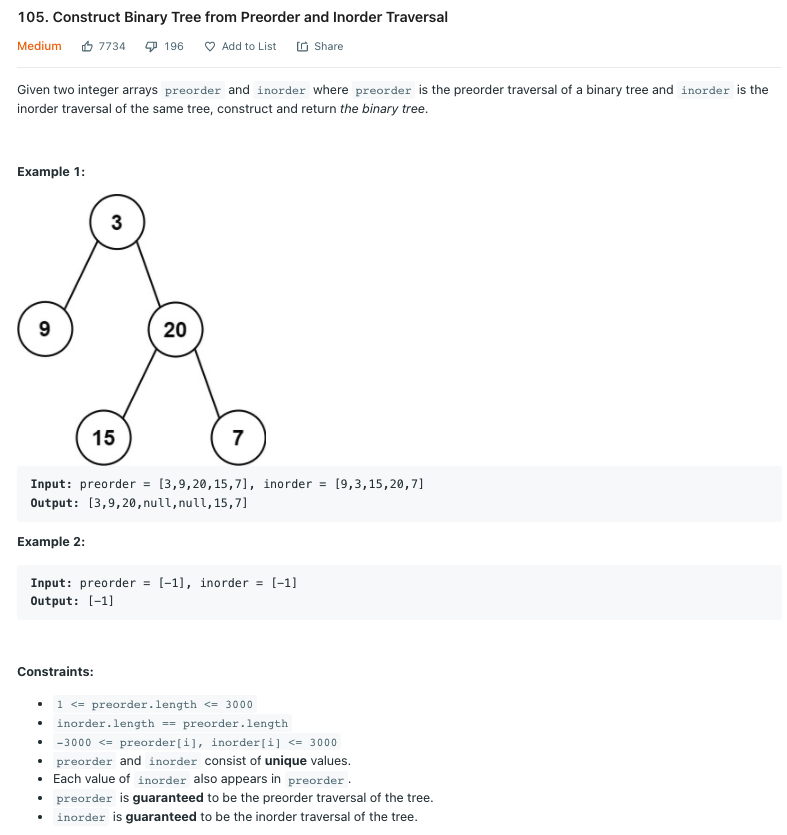
Solution 1 전위 순회 결과로 중위 순회 분할 정복
순회에는 전위, 중위, 후위 순회가 있고 이 중 2가지만 주어져도 이진 트리를 복원할 수 있다.
전위: 1 2 4 5 3 6 7 9 8
중위: 4 2 5 1 7 9 6 8 3
이렇게 주어졌을 때, 전위의 첫번째 값은 부모 노드이다. 즉 전위 순회의 첫번째 결과는 정확히 중위 순회 결과를 왼쪽과 오른쪽으로 분할시키는 역할을 한다. 중위 순회의 분할 정복 문제로 바꾸는 것이다. 두번째로 왼쪽 노드의 2는 중위 순회 결과를 정확히 반으로 가르고, 각각 왼쪽 자식은 4, 오른쪽 자식은 5로 마무리한다.
오른쪽의 경우 3이 첫번째 값인데, 마침 중위 순회에서는 맨 오른쪽에 위치해있다. 이 말은 3의 오른쪽 자식 노드는 존재하지 않는다는 의미이다.
idex = inorder.index(preorder.pop(0))먼저 전위 순회 첫번째 결과를 가져와 중위 순회를 분할하는 인덱스로 한다.
node=TreeNode(inorder[index])
node.left=self.buildTree(preorder, inorder[0:index])
node.right=self.buildTree(preorder, inorder[index+1:])이 값을 현재 노드로 구성하고 이를 기준으로 중위 순회 결과를 쪼개서 왼쪽, 오른쪽으로 각각 마무리도리 때 분할 정복 구조로 재귀 호출하면, 트리를 구성할 수 있다. 전체 코드는 다음과 같다.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if inorder:
index=inorder.index(preorder.pop(0))
node=TreeNode(inorder[index])
node.left=self.buildTree(preorder, inorder[0:index])
node.right=self.buildTree(preorder, inorder[index+1:])
return node
여기서 전위 순회 결과는 pop(0)을 통해 값을 꺼내온다. 큐의 연산이므로 파이썬에서는 데크로 구현 가능하다.
