3D Rigid body(강체)
강체는 위치에 대한 정보와 방향 정보까지 포함하고 있다. 예를 들어 카메라의 경우 x, y, z 위치에서 어떤 방향을 바라보고 있는지를 표현할 수 있다.
Posision(tx, ty, tz) + Orientation(Rx, Ry, Rz) = pose(6DOF)
Coordinate transformation
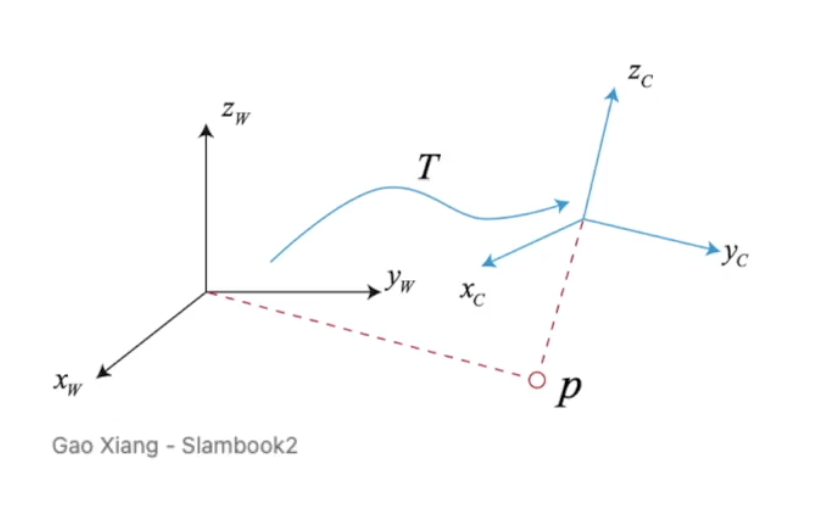
tx, ty, tz, Rx, Ry, Rz의 pose로 관측되는 물체의 경우 world coordinate system에서는 어떤 값을 갖는지는 좌표계 변환을 통해서 알 수 있다. 좌표 변환을 하기 위해서는 두 좌표계 간의 position과 orientation의 변화를 알아야 한다. position의 차이는 이동(translation)으로 알수 있고, orientation의 차이는 회전(rotation)을 통해서 알 수 있다.
강제의 변환(이동)은 Rigid body motion이라고 한다.
3D world는 euclidian world 이고 여기서 사용하는 좌표는 catesian coordinate이다.
다양한 회전 표현법
1. Euler angle
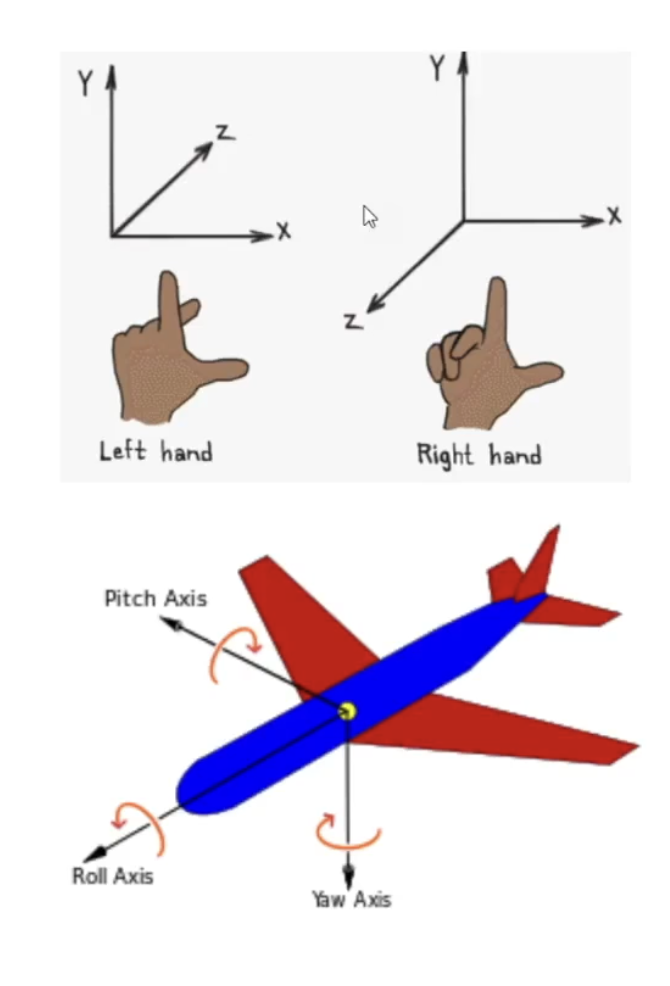
roll, pitch, yaw로 x, y, z 각 축의 회전을 표현하는 방법이다. 3D rotation을 표현하기 위해서는 차례로 변환을 해주어야 한다. 순서가 달라지면 결과도 달라진다. 회전에 대해서 직관적으로 이해하기 쉽다는 장점이 있는 반면에 미분이 불가능하기 때문에 최적화가 어렵다는 단점이 있다.
회전의 경우 순서를 같이 알려주어야 하며, Gradient desent와 같은 방법 사용이 어렵다.
특히, 회전에 따라 다른 축이 원래의 축의 역할을 수행하게 되는 gimbal lock 문제가 나타난다는 것이다.
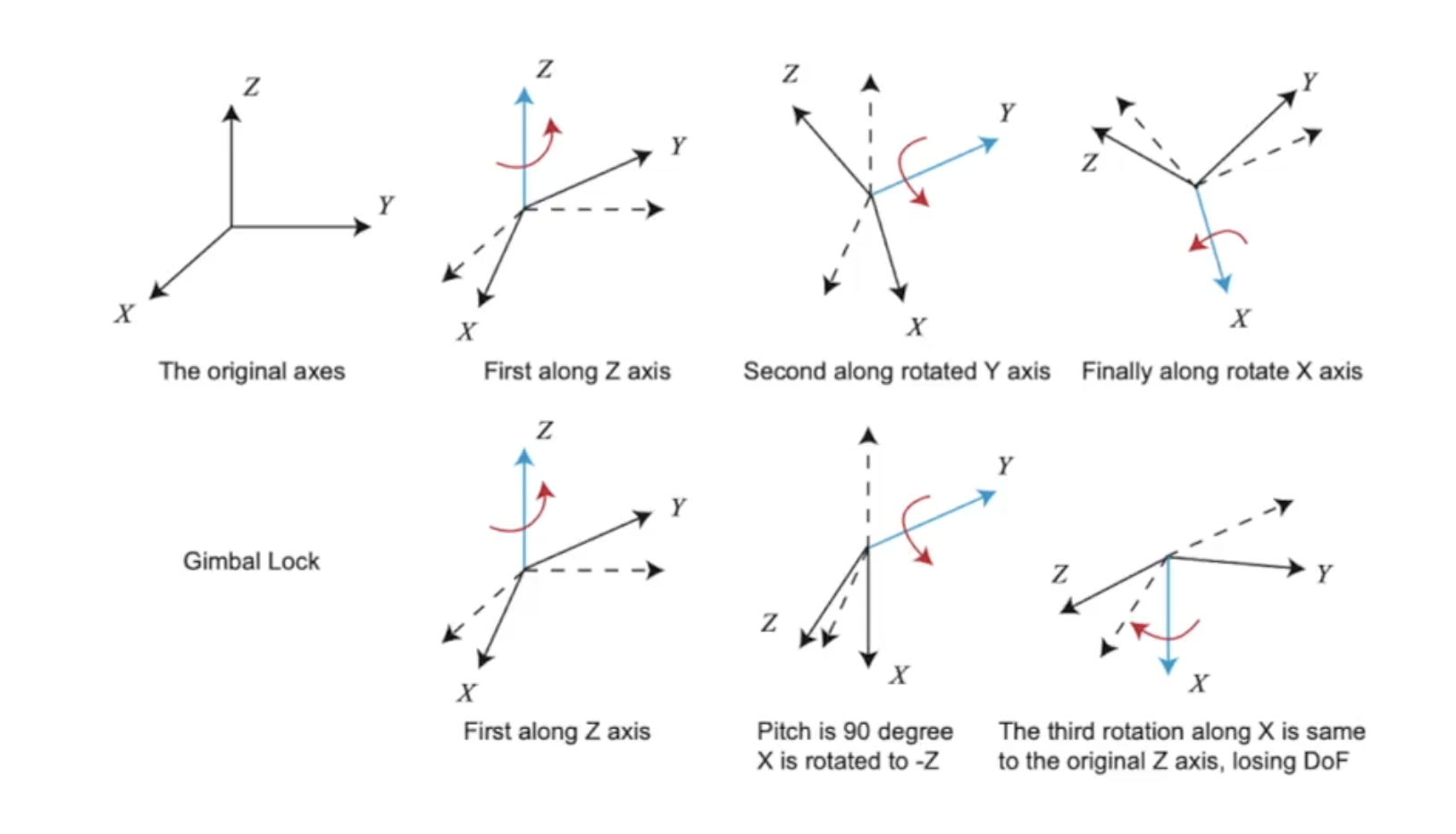
위 그림에서는 회전 전의 z축과 회전 후의 x축의 회전이 동일한 역할을 수행하기 때문에 한 개의 회전 자유도를 잃어버린 것이다. 즉, pitch가 90도가 죄는 지점이 하나의 위치에서 여러 방향으로 미분이 가능한 지점이 생기게 된다. 따라서 회전에 대하여 자연스럽게 설명할 수 없는 문제가 생긴다.
이렇게 회전의 자유도를 잃어버리는 문제를 특이점 문제(singularity problem)이라고 한다.
2. Axis-angle, Angle-axism, Rotation vector, Rodrigues angle
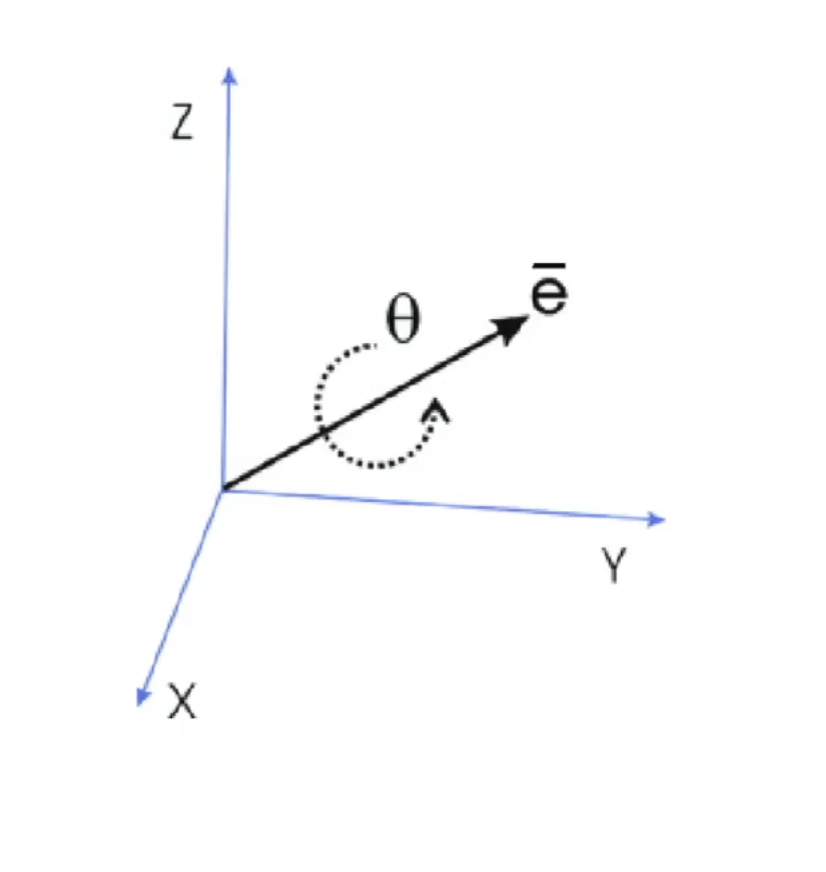
벡터의 축을 기준으로의 회전을 정의한 것이다. 이때 회전하는 축과 회전각의 크기를 합쳐서 축각도 혹은 각도축이라고 부른다. 를 함으로써 회전 자체를 하나의 벡터로 표현이 가능하다.
위 식은 Rodrigues 수식이다. Rodrigues angle의 경우 3개의 값으로 표현할 수 있기 때문에 메모리 효율이 좋다.
3. Quaternion
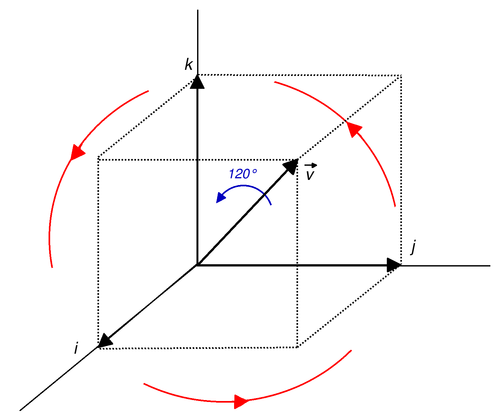
3개의 각 축의 회전을 표현하는 Euler angle에서 알 수 있듯이 3개의 축으로 회전을 설명하는 경우에는 singular problem이 나타나게 된다. 이러한 문제를 해결하기 위해서 복소수를 추가하여 4개의 파라미터로 3차원 공간 상의 회전을 singular problem 문제 없이 표현할 수 있다. 특히 미분이 가능하기 때문에 죄적화 문제로 해결이 가능하다. 다만, 4차원으로 표현되기 때문에 직관적으로 이해하기 어렵다.
4. SO(3) Rotation matrix
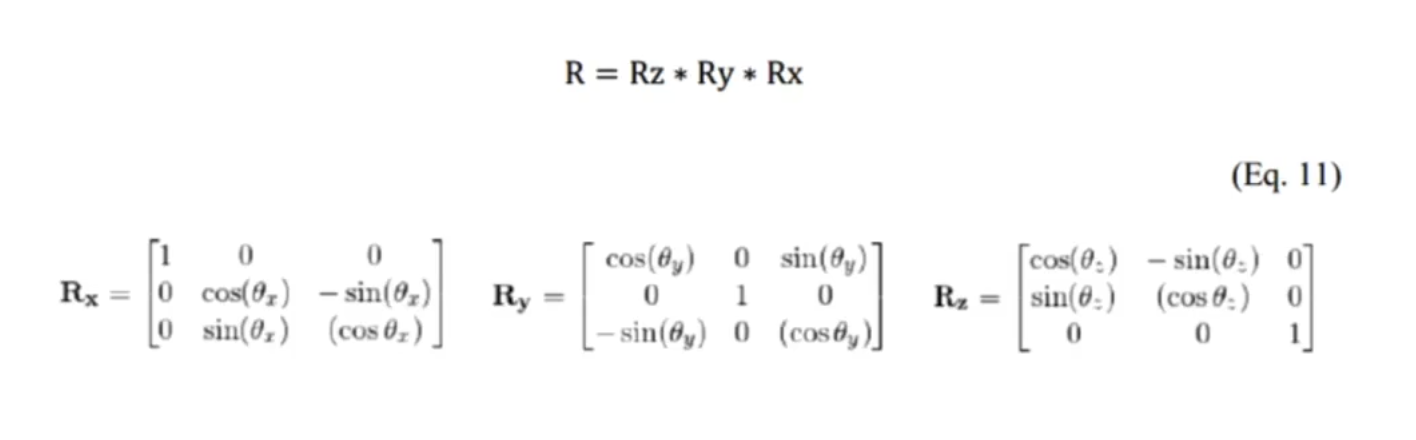
행렬 형태로 회전을 표현하는 방법이다. 다음의 세 가지 조건을 따른다. 첫 번째로 x, y, z가 회전을 해도 회전하기 이전과 마찬가지로 각 축은 수직을 유지해야 한다. 두 번째로 단위 벡터를 유지해야 한다. 마지막을 전치 행렬과 곱했을 때, 단위 행렬이 나와야 한다.
회전을 표현하기 위해서 9개의 매개변수를 사용한다. 또한 SO(3) Matrix의 조건이 많아 이를 충족시키기 어렵다. 미분이 가능해서 jacobian matrix를 얻을 수 있지만 이를 iteration 했을 때, 위 조건을 만족한지는 모른다.
Log map 또는 Exponential map을 통한 Lie algebra 방식을 통해 최적화가 가능하다.
이동(Translation)
회전과 달리 이동은 벡터로 표현할 수 있다. 다만 단위는 동일하게 유지 해주어야 한다.
SE(3) (Special Euclidian group 3D) Transformation matrix
회전과 이동을 한번에 표현하는 방법으로 SO(3)에 Translation 정보를 가지고 있는 형태라고 볼 수 있다.
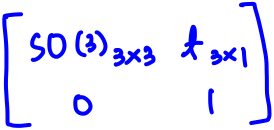
Eigen을 이용한 Rotation 표현
Eigen matrix
#include <Eigen/Dense>
int main(){
# 변수 정의 후 초기화 하는 방법
Eigen::Matrix<double, 2, 3> matrix23_double;
matrix23_double << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0;
# 변수 정의와 동시에 0으로 초기화 하는 방법
Eigen::Matrix3d matrix33_double = Eigen::Matrix3d::Zero();
# 변수의 크기를 가변으로 정의하는 경우
Eigen:: Matrix<double, Eigen::Dynamic, Eigen::Dynamic> matrix_dynamic;
return 0;
}
Eigen vector
int main(){
Eigen::Vector3d vec = {1.0, 2.0, 3.0};
Eigen::Vector3d vec_zeros = Eigen::Vector3d::Zero();
return 0;
}Eigen matrix element access
int main(){
Eigne::Matrix3d mat33;
mat33 << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
for(int row=0; row < mat33.rosw(); ++row){
for(int col=0; cor < mat33.cols(); ++col){
std::cout << mat33(row, col) << "\n";
}
}
return 0;
}Eigen angle-axis
#include <iostream>
#include <cmath>
#include <Eigen/Dense>
#include <Eigen/Geometry>
int main(){
# AngleAxisd에서 마지막 d는 double 타입의 변수를 사용한다는 의미
# M_PI/4.0 => z 축으로 45도 회전을 정의
# Eigen::Vector3d(0.0, 0.0, 1.0)은 단위 벡터를 정의
Eigne::AngleAxisd rotation_vector(M_PI/4.0, Eigen::Vector3d(0.0, 0.0, 1.0));
std::cout << "rotation vector =" << "\n";
std::cout << rotation_vector.maxtix() << "\n";
# SO(3) matrix로 변환해서 표현
std::cout << "\n";
Eigen::Vector3d vector(1.0 , 0.0, 0.0);
Eigne::Vector3d rotated_vector = rotation_vector * vector;
# 벡터를 회전시키기 위해서 곱하기 연산
std::cout << "rotation vector =" << "\n";
std::cout << rotated_vector.transpose() << "\n";
return 0;
}Eigen quaternion
#include <Eigen/Dense>
#include <Eigen/Geometry>
int main(){
Eigne::AngleAxisd rotation_vector(M_PI/4.0, Eigen::Vector3d(0.0, 0.0, 1.0));
Eigen::Quaterniond guat = Eigne::Quaternion(rotation_vector);
Eigen::Vector3d vector(1.0, 0.0, 0.0);
std::cout << "quaternion =" << quat.coffes().tranpose() << "\n";
std::cout << "\n";
std::cout << "rotated vector =" << (quat * vector).transpose() << "\n";
return 0;
}Coordinate transformation example
작성중
