코드 및 내용 출처 : Do it 딥러닝 입문
1. 문제 해결을 위한 당뇨병 환자 데이터 준비
- 목표 : 당뇨병 환자의 1년 후 병의 진전된 정도를 예측하는 모델 만들기
vscode 에서 scikit-learn이 설치되어 있지 않은 경우
pip install scikit-learn # 사이킷런 설치import sklearn
print(sklearn.__version__) # 버전확인1-1. 입력과 타겟 데이터의 크기 확인하기
# 입력데이터와 타겟 데이터 크기 확인하기
print(diabetes.data.shape, diabetes.target.shape)
# 입력 데이터 확인해보기
print(diabetes.data[0:3]) # 입력데이터 앞부분의 3개 샘플 확인
# 타겟 데이터 확인해보기
print(diabetes.target[:3]) # 타겟데이터의 3개 샘플 확인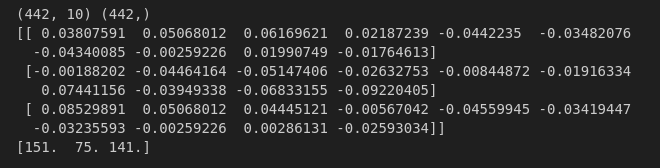
- data는 442 x 10 크기의 2차원 배열이며, target은 442개의 요소를 가진 1차원 배열이다
- 입력데이터를 보면 10개의 features 값을 갖고 있는 것을 확인할 수 있다.
- 타겟데이터는 1개의 값을 갖는다.
당뇨병 데이터는 10개의 features와 이에 대응하는 1개의 target 값으로 구성되어 있다
1-2. 당뇨병 환자 데이터 시각화 해보기
import matplotlib.pyplot as plt
plt.scatter(diabetes.data[:,2], diabetes.target)
plt.xlabel('x')
plt.ylabel('y')
plt.show()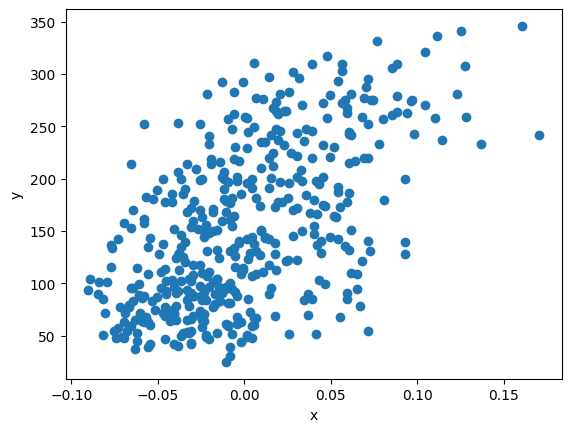
- x축은 입력데이터의 세 번째 특성이며, y축은 타겟데이터이다.
위의 그래프를 확인해보면, 입력데이터의 세 번째 특징과 타겟 데이터 사이에 정비례 관계가 있음을 확인할 수 있다
두 데이터가 정비례 관계라는 것은 선형 회귀를 공부하기에 적합할 수 있으므로, 이 데이터들을 사용하여
선형 회귀 알고리즘과경사 하강법에 대해 알아보기
2. 경사하강법 실습
선형 회귀의 목표 : 입력 데이터(x)와 타겟 데이터(y)를 통해
기울기와절편을 찾는 것
- 위에서 산점도 그래프를 잘 표현하는 직선의 방정식을 찾는 것이 회귀 알고리즘의 목표
- 이 방법 중 하나가
경사 하강법(gradient descent)이다
2-1. 예측값이란?
-
입력과 출력 데이터 (x, y)를 통해 규칙을 발견하여 모델을 만들었을 때, 새로운 입력 값을 넣으면 출력이 나온다
그 때의 출력값이 모델을 통해예측한 값이다.: 예측 값
w = 가중치
b = 절편 -
우리가 찾고 싶은 것은 훈련 데이터 (x, y)에 잘 맞는 w와 b이다
- 무작위로 w 와 b 를 정한다 (무작위로 모델 만들기)
- x에서 샘플 하나를 선택하여 을 계산하기 (무작위로 모델 에측하기)
- 예측 값인 과 진짜 데이터인 y를 비교하기
- 이 y 와 가까워지도록 w, b를 조정하기 (모델 조정하기)
- 모든 샘플을 처리할 때까지 2~4를 반복
2-2. 코드 실습
1. 무작위로 w 와 b 를 정한다 (무작위로 모델 만들기)
x = diabetes.data[:,2]
y = diabetes.target
w = 1.0
b = 1.02. 훈련데이터의 펏 번째 샘플로 예측값 구하기
타겟(실제 값)과 예측 데이터 비교하기
y_hat = x[0]*w + b
print('임의의 값을 사용한 모델의 예측 값:',y_hat)
print('실제 타겟 값:', y[0])
# 임의의 값을 사용한 모델의 예측 값: 1.0616962065186832
# 실제 타겟 값: 151.0예측 값과 실제 타겟 값의 차이가 약 150이다.
w 와 b 를 임의의 값으로 설정했기에 예측 결과가 잘 나오지 않는 것은 당연함
=> w 와 b를 조금씩 바꿔보면서 예측 값이 증가 or 감소하는지 살펴보기
3. w 값 조절하기
w_inc = w + 0.1
y_hat_inc = x[0]*w_inc + b
print(y_hat_inc)
# 1.0678658271705517-
w값을 0.1 증가시켰지만 예측 값은 크게 변화하지 않은 것을 확인할 수 있다.
-
그렇다면 w 값을 0.1 만큼 증가시켰을 때 예측 값의 변화를 확인해보기
w_rate = (y_hat_inc - y_hat) / (w_inc - w)
print('w의 변화율:', w_rate)
# w의 변화율: 0.06169620651868429
예측 값 (y_hat)의 값은 실제 타겟 값 (y) 보다 작기 때문에예측 값 (y_hat)을 증가시켜야 함
- 이 때의 변화율은
양수이므로 w 값을 증가시키면y_hat값을 증가시킬 수 있다.그렇다면 변화율이
음수일 때y_hat값을 증가시켜야 한다면?
=> w 값을 감소시키면 된다
4. 변화율로 가중치 업데이트 하기
- 가중치 w를 업데이트 하는 방법은
w + w_rate이다.
w_new = w + w_rate
print(w_new)
# 1.06169620651868435. 변화율로 절편 업데이트 하기
b_new = b + 1
print(b_new)
# 2.0위의 방법들은
1.y_hat이y에 한참 미치지 못하는 값인 경우, w와 b를 더 큰 폭으로 수정할 수 없다
2.y_hat이y보다 커지면y_hat을 감소시키지 못한다
3. 오차 역전파로 가중치와 절편을 더 적절하게 업데이트
3.1 오차와 변화율을 곱하여 가중치 업데이트하기
주어진 첫 번째 샘플로 모델을 학습하는 방법
여기서, 모델이 예측한 값과 실제 값의 차이(오차)를 계산하고, 이 오차를 바탕으로 가중치 𝑤와 절편 𝑏를 업데이트
err = y[0] - y_hat # 예측 값과 실제 값의 차이 (오차)
w_new = w + w_rate * err # 가중치 업데이트
b_new = b + 1 * err # 절편 업데이트
print(w_new, b_new)
# 10.250624555903848 150.93830379348133.2 두 번째 샘플을 사용하여 가중치와 절편 업데이트하기
다음으로 두 번째 샘플을 사용하여 오차를 계산하고, 이를 바탕으로 새롭게 업데이트된 가중치와 절편을 구하기
y_hat = x[1] * w_new + b_new # 두 번째 샘플로 예측 값 계산
err = y[1] - y_hat # 오차 계산
w_rate = x[1] # 가중치 변화율
w_new = w_new + w_rate * err # 가중치 업데이트
print(w_new, b_new)
# 14.132317616380695 150.93830379348133.3 전체 샘플을 반복하여 학습하기
경사하강법은 전체 훈련 데이터를 사용하여 반복적으로 학습하는 방식이다
각 샘플에 대해 모델의 예측 값을 구하고, 오차를 계산한 후, 가중치와 절편을 계속 업데이트하는 과정을 반복하기
for x_i, y_i in zip(x, y): # 입력 데이터와 타겟 데이터를 순차적으로 사용
y_hat = x_i * w + b # 예측 값 계산
err = y_i - y_hat # 오차 계산
w_rate = x_i # 가중치 변화율
w = w + w_rate * err # 가중치 업데이트
b = b + 1 * err # 절편 업데이트
print(w, b) # 최종 가중치와 절편 출력
# 587.8654539985616 99.40935564530943.4 학습된 모델이 데이터를 잘 표현하는지 확인하기
훈련이 끝난 후, 학습된 모델이 주어진 데이터를 잘 표현하는지 시각적으로 확인
plt.scatter(x, y) # 실제 데이터의 산점도
pt1 = (-0.1, -0.1 * w + b) # 선형 모델의 시작점
pt2 = (0.15, 0.15 * w + b) # 선형 모델의 끝점
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]]) # 모델의 직선
plt.xlabel('x') # x축 라벨
plt.ylabel('y') # y축 라벨
plt.show() # 그래프 출력
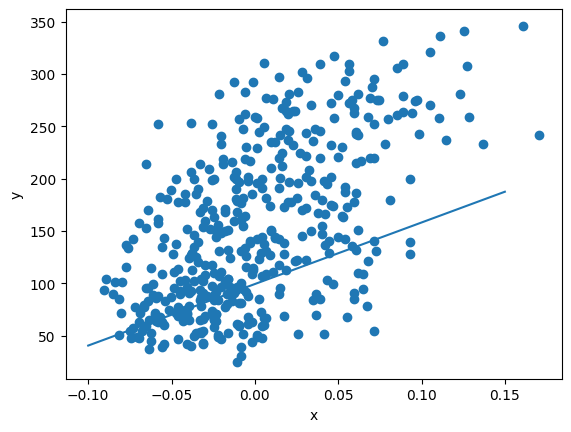
3.5 여러 에포크 반복하기
보통 경사하강법은 데이터를 한 번만 학습하는 것이 아니라 여러 번 반복하며 학습을 진행
이를 에포크(epoch)라고 하며, 학습 횟수가 많아질수록 모델이 점차적으로 개선된다
for i in range(1, 100): # 100번 반복하며 학습 진행
for x_i, y_i in zip(x, y):
y_hat = x_i * w + b # 예측 값 계산
err = y_i - y_hat # 오차 계산
w_rate = x_i # 가중치 변화율
w = w + w_rate * err # 가중치 업데이트
b = b + 1 * err # 절편 업데이트
print(w, b) # 최종 가중치와 절편 출력
# 학습된 모델 시각화
plt.scatter(x, y)
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()
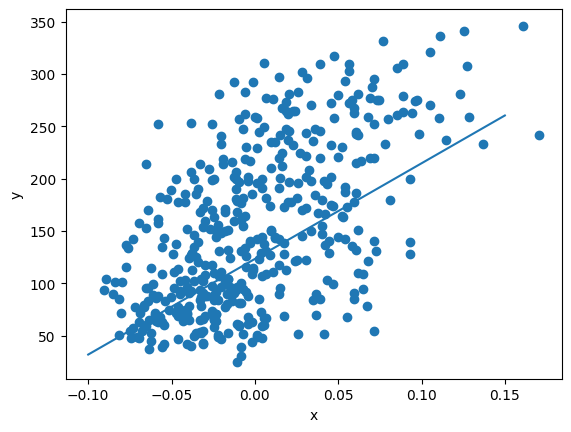
경사하강법은 기계학습에서 손실을 최소화하기 위한 대표적인 최적화 알고리즘
