1. 로지스틱 회귀란

로지스틱 회귀는 이진 분류 문제를 해결하는 데 주로 사용되는 지도 학습 알고리즘이다.
이는 회귀라는 이름이 붙어 있지만, 실제로는 분류 알고리즘으로, 주어진 데이터를 기반으로 특정 사건이 일어날 확률을 예측한다.

로지스틱 회귀(Logistic Regression)는 종속 변수가 범주형(보통 두 가지 범주로 나뉘는 이진 분류)인 경우에 사용된다.

• 예시) 이메일이 스팸인지 아닌지, 환자가 질병에 걸렸는지 아닌지를 예측
• 로지스틱 회귀는 선형 회귀와 달리, 결과값이 0과 1 사이의 확률로 나오며, 특정 임계값을 기준으로 분류를 수행한다.

수식적으로 로지스틱 회귀는 다음과 같은 시그모이드 함수(Sigmoid Function)를 통해 선형 모델의 출력 값을 확률로 변환한다.

2. 시그모이드 함수란

• 시그모이드(sigmoid) 함수
  로지스틱 회귀에서 핵심적으로 사용되는 시그모이드 함수는 선형 회귀의 예측값을 확률로 변환하는 함수이다

  $S(x) = \frac{1}{1 + e^{-x}}$

• 시그모이드 함수의 특징

  1. 출력 범위가 0과 1 사이
     입력값이 작으면 0에 가까운 값, 크면 1에 가까운 값을 출력
  2. S자 형태
     함수가 S자 모양의 곡선을 그리며, 0.5를 기준으로 예측값이 이진 분류로 나뉨
  3. 확률 해석 가능
     시그모이드 함수의 출력값을 0에서 1까지의 확률로 해석 가능

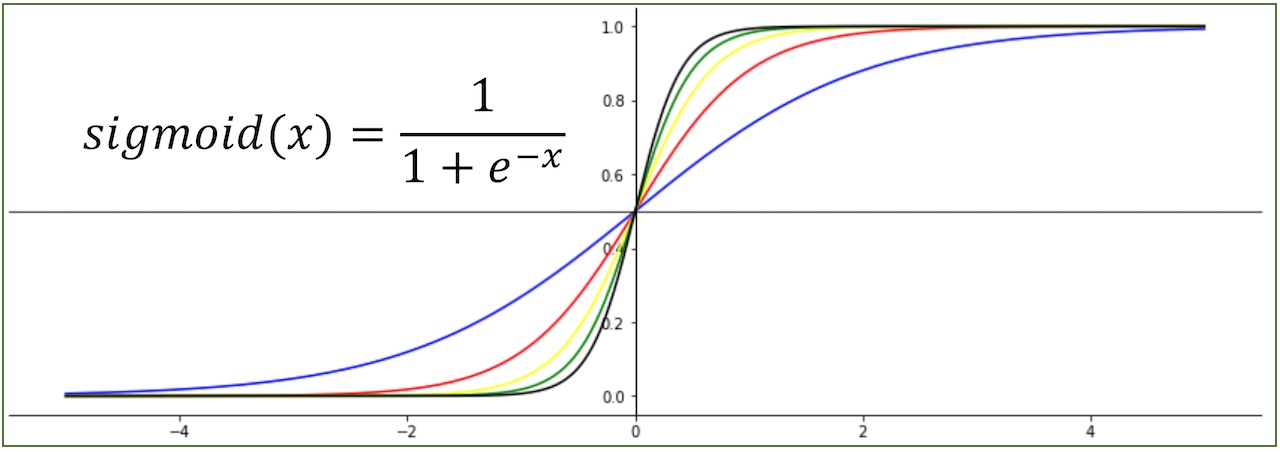
이미지출처: http://taewan.kim/post/sigmoid_diff/#google_vignette

3. 로지스틱 회귀 예시 코드

import numpy as np  # 배열 및 수학적 연산을 위한 라이브러리
import tensorflow as tf  # 딥러닝 프레임워크인 TensorFlow를 불러옴
import matplotlib.pyplot as plt  # 데이터 시각화를 위한 라이브러리

from tensorflow.keras import Sequential  # 신경망 모델을 순차적으로 쌓을 수 있는 클래스
from tensorflow.keras.layers import Dense  # 완전 연결(Dense) 레이어를 사용하기 위한 클래스

# 학습 데이터를 정의
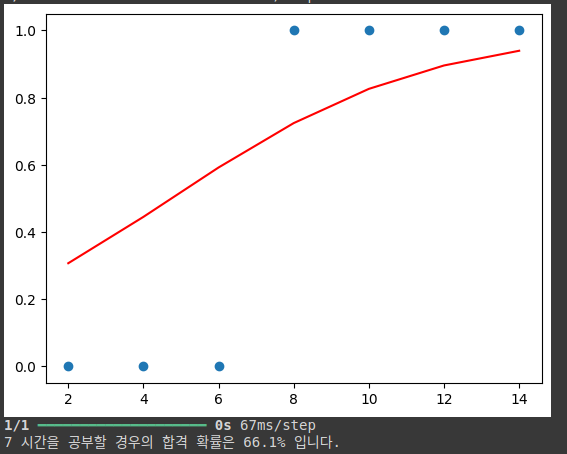
x = np.array([2,4,6,8,10,12,14])  # 공부 시간
y = np.array([0,0,0,1,1,1,1])  # 합격 여부 (0: 불합격, 1: 합격)

# Sequential 모델을 생성 (순차적으로 레이어를 추가하는 방식)
model = Sequential()
model.add(Dense(1, input_dim=1, activation='sigmoid'))  # 하나의 입력, 시그모이드 활성화 함수를 사용하는 Dense 레이어 추가
# - Dense(1): 출력 뉴런의 개수 1개
# - input_dim=1: 입력 차원(공부 시간)을 1로 지정
# - activation='sigmoid': 시그모이드 함수로 출력값을 확률로 변환

model.compile(optimizer='sgd', loss='binary_crossentropy')  # 모델을 컴파일. 최적화 알고리즘으로 SGD(Stochastic Gradient Descent) 사용
# - optimizer='sgd': 확률적 경사 하강법을 사용하여 모델을 학습
# - loss='binary_crossentropy': 이진 분류 문제이므로 손실 함수로 이진 크로스 엔트로피 사용

model.fit(x, y, epochs=1000)  # 모델을 학습. 1000번의 반복(에포크) 동안 데이터에 맞게 학습
# - fit(x, y): x와 y 데이터를 사용하여 모델 학습
# - epochs=1000: 전체 데이터셋을 1000번 반복 학습

# 시각화를 위한 코드
plt.scatter(x, y)  # 공부 시간(x)과 합격 여부(y)를 산점도로 표시
plt.plot(x, model.predict(x), 'r')  # 모델이 예측한 확률 값(시그모이드 결과)을 빨간 선으로 그리기
plt.show()  # 그래프를 출력

# 특정 공부 시간(hour)에 대한 합격 확률 예측
hour = 7  # 공부 시간을 7시간으로 설정
prediction = model.predict(np.array([hour]))  # 7시간 공부했을 때의 합격 확률을 예측

# 예측 결과 출력
print('%.f 시간을 공부할 경우의 합격 확률은 %.01f%% 입니다.' % (hour, prediction*100))
# 예측 확률을 퍼센트로 변환하여 출력

4. 로지스틱 회귀와 선형 회귀의 차이

로지스틱 회귀는 선형 회귀와 달리, 출력을 확률로 변환하는 분류 알고리즘이다.
선형 회귀에서는 입력 변수와 종속 변수 사이의 선형 관계를 찾고 이를 이용해 값을 예측하지만, 로지스틱 회귀는 결과값이 특정 범주(0 또는 1)에 속할 확률을 예측한다.
이러한 확률 값은 시그모이드 함수를 통해 출력되며, 이 함수는 로그 오즈 비율(Log-Odds)을 확률로 변환하는 핵심적인 역할을 합니다.