1. 인공지능의 시작 : 퍼셉트론(Perceptron)
-
퍼셉트론(Perceptron)이란?
퍼셉트론은 1950년대 말, 프랭크 로젠블랫(Frank Rosenblatt)이 개발한기계 학습 모델로, 인공지능 발전의 첫걸음- 뇌의 뉴런이 작동하는 원리를 모방한 간단한 형태의 인공 신경망(Artificial Neural Network)
- 퍼셉트론은 입력을 받아 단순한 연산을 통해 출력을 생성
- 퍼셉트론에 경사하강법을 도입해 최적의 경계선을 그릴 수 있게 한
아달라인(Adaline)이 개발됨
-
퍼셉트론의 구조는 입력층과 출력층이라는 2개의 층으로 구성되는 단순한 구조
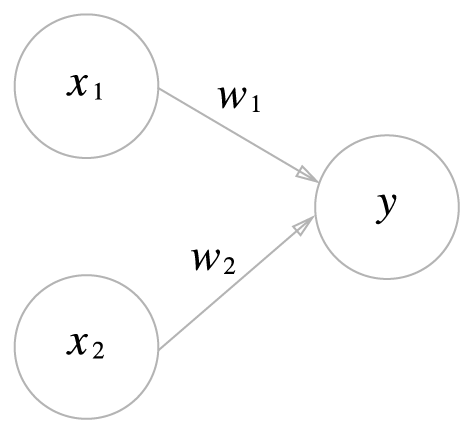
x1, x2 : 입력 신호
y : 출력신호
w1, w2 : 가중치 weight
그림에서 원은 뉴런 혹은 노드
1-1. 퍼셉트론의 한계 (XOR 문제)
- 퍼셉트론의 문제점
퍼셉트론은 입력과 출력을선형적으로 분리할 수 있는 문제에서는 매우 잘 작동하지만, 복잡한 문제를 해결하는 데에는 한계가 있다- 대표적인 예가
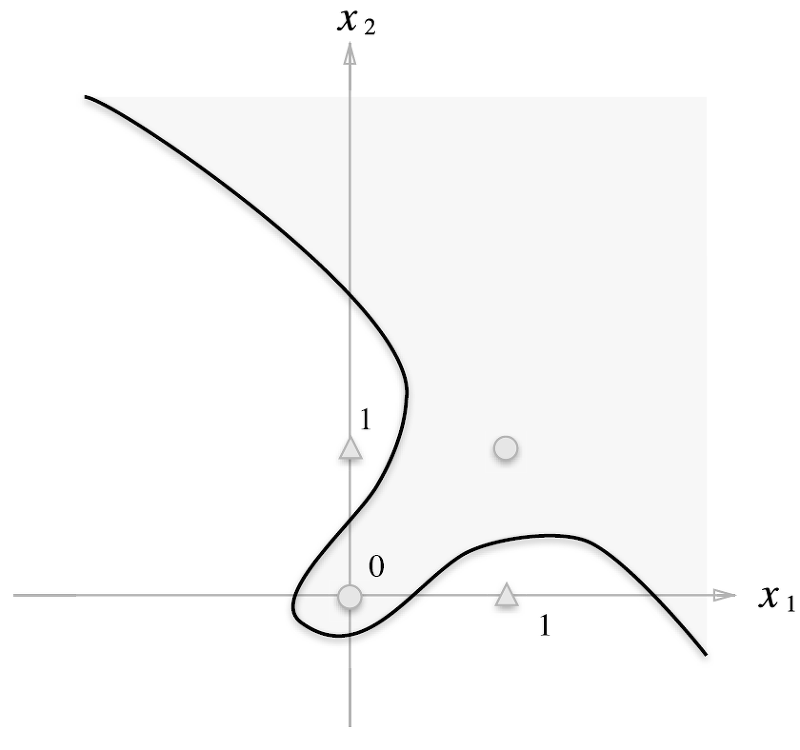
XOR 문제 - XOR는 두 입력값이 다를 때만 1을 출력하는 논리 연산
하지만 이 문제는 선형적으로 분리할 수 없기 때문에 퍼셉트론으로 해결할 수 없다 - XOR 문제는 (0, 1), (1, 0)일 때만 1을 출력하고, 그 외에는 0을 출력하는 형태
XOR 문제는 선형 분리가 불가능하기 때문에 퍼셉트론의 기본 구조는 이러한 XOR 문제를 풀 수 없다
- 대표적인 예가
- 이 문제는 인공지능 연구의 초기 단계에서 큰 도전 과제
퍼셉트론의 한계를 극복하기 위한 새로운 접근이 필요함을 보여준다
이를 해결하기 위해다층 퍼셉트론(Multilayer Perceptron, MLP)이 도입되었다.
2. 다층 퍼셉트론(Multilayer Perceptron, MLP)
2-1. 다층 퍼셉트론이란?
다층 퍼셉트론(Multilayer Perceptron, MLP)은 퍼셉트론의 한계를 극복하기 위해 제안된 모델- 다층 퍼셉트론은 입력층, 은닉층(hidden layer), 출력층으로 구성된 다층 신경망을 통해 복잡한 문제도 해결할 수 있다
- 퍼셉트론은 단일 직선으로 데이터를 구분할 수 있는 선형 문제만 풀 수 있었지만, 다층 퍼셉트론은 비선형 문제도 해결할 수 있는 강력한 도구
- 이를 통해 XOR 문제와 같은 비선형적 문제도 풀 수 있다
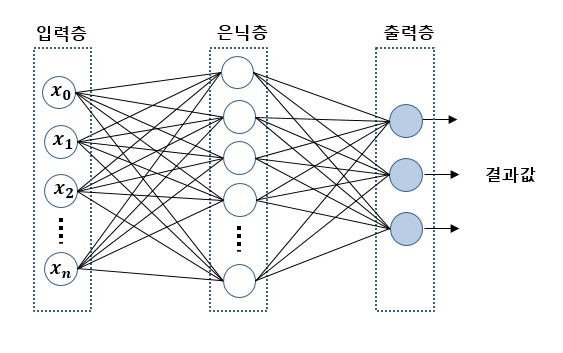
2-2. 다층 퍼셉트론의 구조
입력층 (Input Layer): 입력 데이터를 받아들이는 층으로, 각 뉴런은 주어진 데이터를 모델에 전달하는 역할을 한다은닉층 (Hidden Layer): 입력 데이터를 처리하고 학습하는 층으로 이 층에서 복잡한 패턴이 학습된다.
은닉층이 한 개일 수도, 여러 개일 수도 있다출력층 (Output Layer): 예측 또는 분류 결과를 출력하는 층
출처 : https://hi-guten-tag.tistory.com/53
2-3. 왜 은닉층이 필요한가?
단일 퍼셉트론은 선형적으로 분리 가능한 문제만 해결할 수 있다.
하지만
비선형 문제는 직선 하나로 구분할 수 없다.
이를 해결하기 위해 은닉층을 사용하여 입력 데이터를 변환하고, 이를 통해 더욱 복잡한 패턴을 학습할 수 있게 된다.
3. 딥러닝의 태동 : 오차 역전파 (Backpropagation)
다층 퍼셉트론(Multilayer Perceptron, MLP)은 복잡한 비선형 문제를 해결할 수 있지만, 어떻게 학습할 것인지가 중요한 과제임- MLP가 성공적으로 학습할 수 있게 만든 핵심 알고리즘이 바로
오차 역전파(Backpropagation)
오차 역전파는 출력층에서 발생한 오차를 역방향으로 전달하여 각 층의 가중치를 조정하는 방식으로 학습을 진행
이를 통해 네트워크가 입력에 따라 최적의 출력을 낼 수 있도록 가중치가 업데이트된다
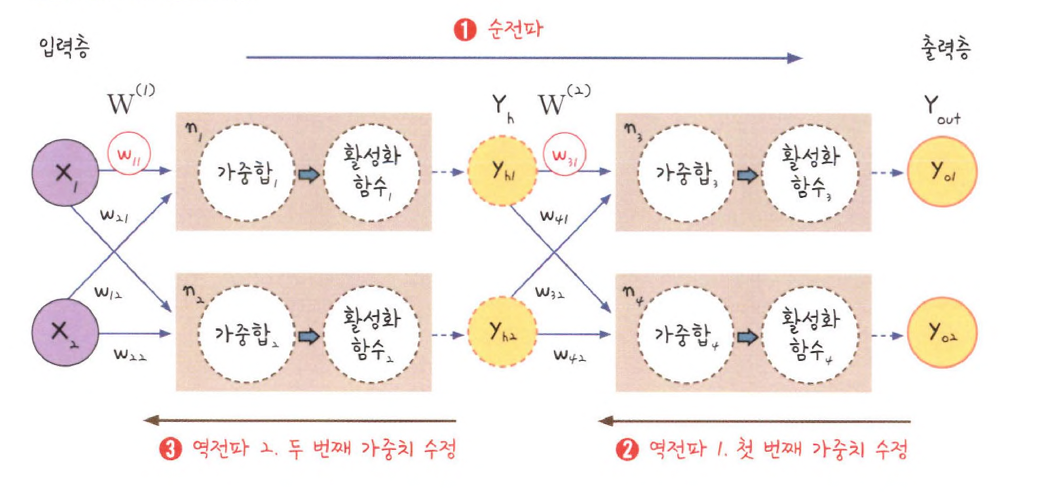
오차 역전파 알고리즘은 다음과 같은 과정으로 동작
순전파(Forward Propagation): 입력 데이터가 입력층에서 시작하여 은닉층을 거쳐 출력층까지 전달되며, 예측 값을 계산오차 계산: 예측값과 실제 값(정답) 사이의 차이를 측정하여 오차(손실)를 계산
이때 손실 함수(Loss Function)를 사용하여 오차의 크기를 측정역전파(Backpropagation): 출력층에서부터 역방향으로 오차를 전달하면서 각 뉴런의 가중치를 업데이트
이를 통해 가중치가 손실을 줄이는 방향으로 조정됨가중치 업데이트: 경사 하강법(Gradient Descent)을 사용하여 손실 함수의 기울기를 따라 가중치를 조정해 나감
이미지 출처 : https://jominseoo.tistory.com/44
3-1. 활성화 함수의 문제: 시그모이드와 기울기 소실(Vanishing Gradient)
오차 역전파 알고리즘은 MLP를 학습시키는 중요한 역할을 하지만, 초기 딥러닝 연구에서 큰 문제에 직면하게 된다
그 중 하나가 기울기 소실 문제(Vanishing Gradient Problem) 이다.
-
기울기 소실 문제
역전파 과정에서 층이 깊어질수록, 즉 은닉층이 많아질수록 오차를 전파할 때 기울기(gradient)가 점점 작아지며, 결국 가중치 업데이트가 제대로 이루어지지 않는 문제가 발생 -
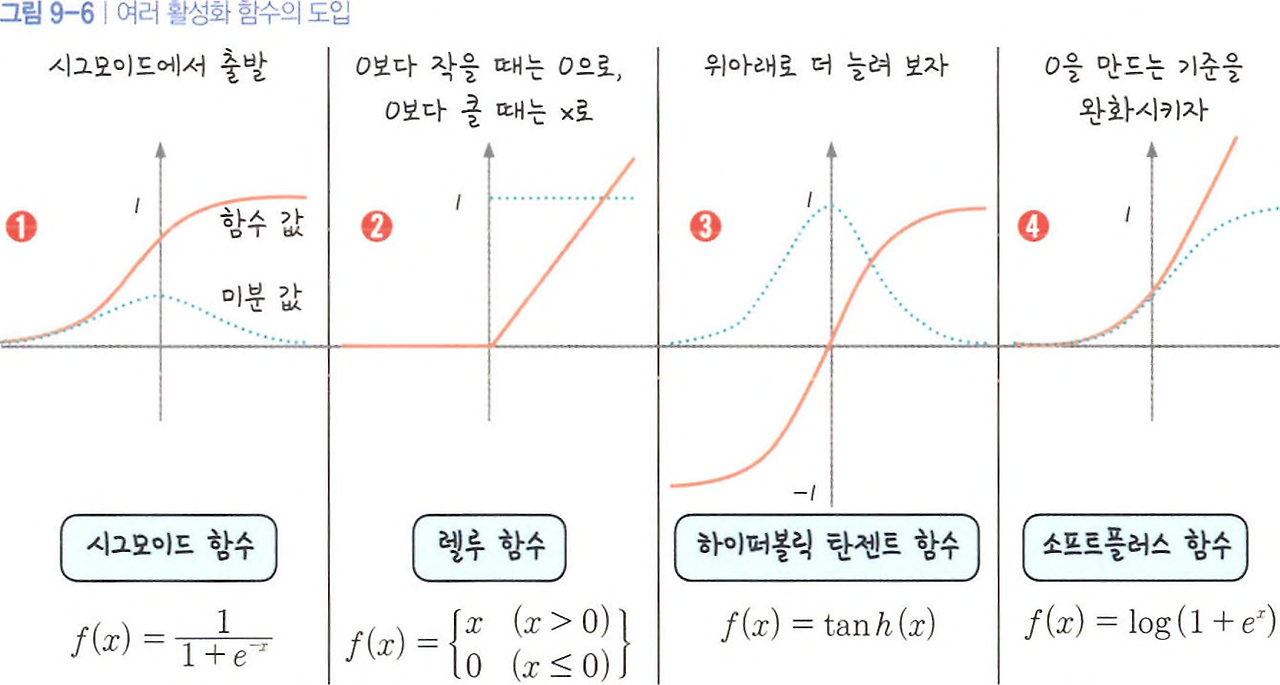
이 문제는 특히 시그모이드 함수와 같은
비선형 활성화 함수를 사용할 때 심각하게 발생함
- 시그모이드 함수를 미분하면 최대치가 0.25 이므로 계속 곱하다보면 0에 가까워진다
- 따라서 여러 층을 거칠수록 기울기가 거의
0에 수렴하며 기울기가 사라진다
이로 인해 역전파를 통해 전달되는 기울기가 사라지면서 가중치가 거의 업데이트되지 않는 문제가 발생하게 됨
3-2. 새로운 활성화 함수: ReLU (Rectified Linear Unit)
- 기울기 소실 문제를 해결하기 위해 ReLU(Rectified Linear Unit) 라는 새로운 활성화 함수가 등장
이미지 출처 : https://jominseoo.tistory.com/44
ReLU는 기울기 소실 문제를 완화하고, 특히 깊은 신경망에서 훨씬 효율적으로 학습할 수 있도록 도와줌
-
ReLU: ReLU는 입력이 0 이하일 때는 0을 출력하고, 그 외에는 입력값 그대로를 출력하는 비선형 함수- 이를 통해 기울기 소실 문제를 완화하고 더 깊은 네트워크에서도 효과적으로 학습할 수 있다
-
ReLU의 특징:
계산이 간단하고 빠르며, 기울기 소실 문제를 해결하는 데 큰 도움을 줌
주의할 점:
- ReLU와 시그모이드는 층의 위치와 역할이 다르다
ReLU는 이중 분류 문제의 은닉층에서 자주 사용되지만, 출력층에서는 여전히시그모이드 함수가 사용되는 것이 일반적
3-3. 고급 경사 하강법의 등장
딥러닝의 또 다른 문제는 속도와 정확도이다.
- 네트워크가 깊어지면서 학습 속도가 느려지거나, 최적의 결과를 얻지 못하는 경우가 발생할 수 있다.
- 이를 해결하기 위해 고급 경사 하강법(Optimizers) 이 도입되었음
- 이러한 기법들은 단순한 경사 하강법보다 더 효율적이며, 빠르고 안정적으로 학습을 도와줌
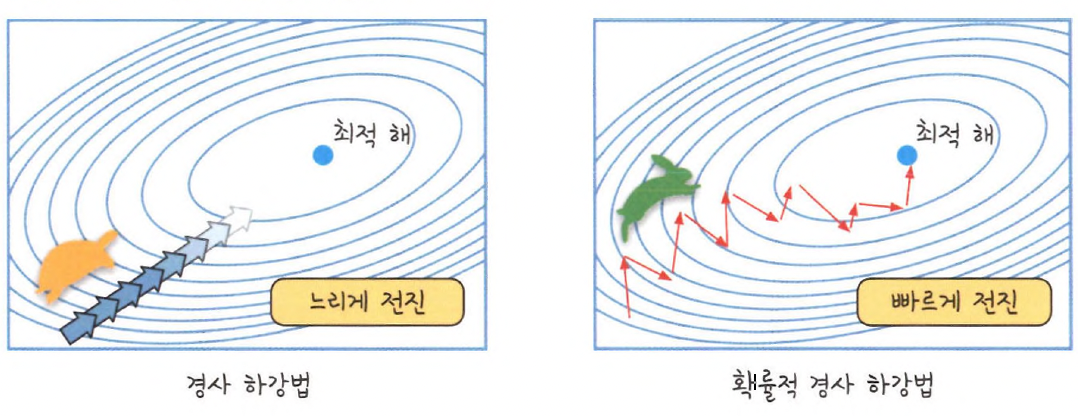
확률적 경사 하강법(Stochastic Gradient Descent, SGD):
전체 데이터가 아닌 랜덤하게 선택된 일부 데이터(미니배치)를 사용하여 가중치를 업데이트함으로써 학습 속도를 향상시킴
매번 일부 데이터를 사용하기 때문에 계산량이 줄고, 더 빠르게 학습할 수 있음
- 진폭이 크고 불안정해 보일 수 있지만 속도가 확연히 빠르고 최적 해에 근사한 값을 찾아냄
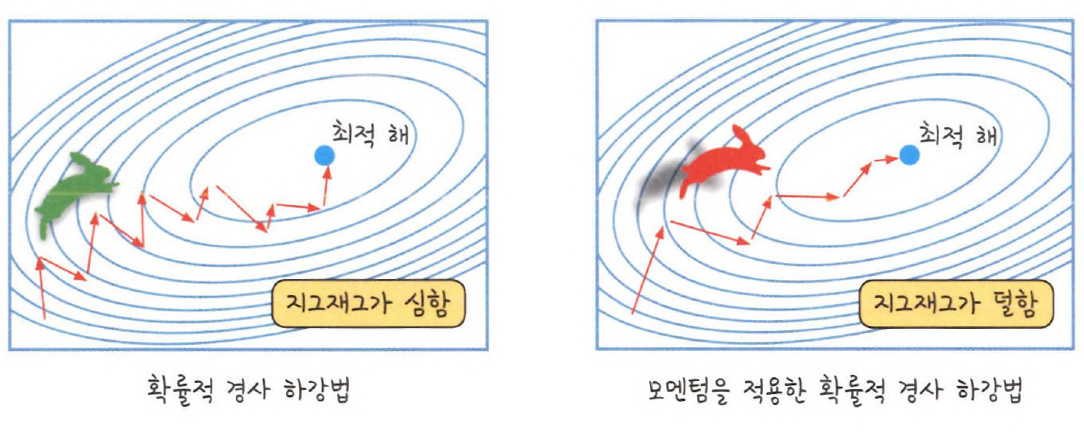
모멘텀(Momentum):
경사 하강법이 최적의 값을 찾는 동안 흔들리는 문제(진동)를 해결하기 위해 모멘텀을 사용한다.
모멘텀은 이전 단계의 기울기 정보를 사용해 학습 속도를 더 빠르게 하고, 더 안정적인 경로로 최적화할 수 있게 해줌.
- 확률적 경사 하강법에
탄력을 더해준다고 생각하면 됨
Adam(Adaptive Moment Estimation):
Adam은 경사 하강법의 발전된 형태로, 학습 속도와 정확도를 동시에 개선하는 알고리즘
Adam은 학습 속도에 대한 자동 조정 기능을 제공하며, 모멘텀과 학습률을 동시에 고려해 가중치를 업데이트
이는 딥러닝에서 가장 널리 사용되는 옵티마이저 중 하나이다
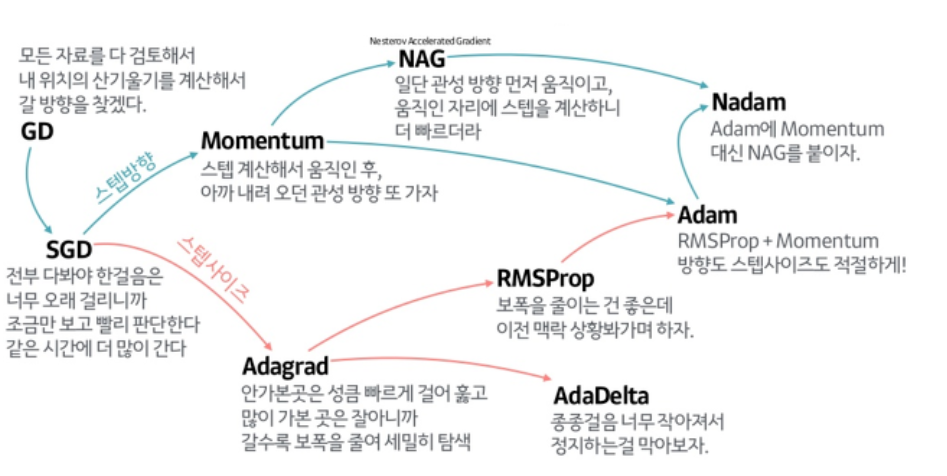
(이미지 출처 : https://sohyunwriter.tistory.com/34)
4. Summary
-
다층 퍼셉트론(MLP)과 비선형 문제 해결
- 다층 퍼셉트론(Multilayer Perceptron) 은 여러 개의 은닉층을 가지고 있으며, 이로 인해 비선형 문제를 해결할 수 있음
- 다층 퍼셉트론에서 중요한 것은, 각 층이 입력값을 처리할 때
비선형성을 부여하여 복잡한 패턴을 학습할 수 있도록 돕는 것
-
활성화 함수(Activation Function)
- 활성화 함수는 입력값을 비선형적으로 변환해주는 역할
이를 통해 신경망이 비선형 문제도 해결할 수 있음 - 주요 활성화 함수:
시그모이드(Sigmoid): 출력값을 0과 1 사이로 변환하여 이진 분류 문제에서 사용.ReLU(Rectified Linear Unit): 은닉층에서 자주 사용되며, 기울기 소실 문제를 해결하고 학습을 빠르게 진행.소프트맥스(Softmax): 다중 분류 문제에서 사용되어 각 클래스의 확률을 계산.
- 활성화 함수는 입력값을 비선형적으로 변환해주는 역할
-
옵티마이저(Optimizer)
- 옵티마이저는 가중치를 업데이트하는 데 중점을 두며, 가중치를 최적화하는 역할
경사 하강법을 기반으로 가중치를 최적화하고, 이를 통해 손실 함수의 값을 최소화
-
옵티마이저의 발전 과정
경사 하강법(Gradient Descent): 기본적인 가중치 업데이트 방식.확률적 경사 하강법(SGD): 전체 데이터 대신 일부 샘플을 이용해 빠르고 효율적인 학습을 가능하게 함.모멘텀(Momentum): 학습 방향을 안정적으로 잡아주며, 진동 문제를 해결.Adam(Adaptive Moment Estimation): 가장 널리 사용되는 옵티마이저 중 하나로,학습률을 자동으로 조정하여 빠르고 안정적으로 가중치를 최적화함.
최종 요약:
활성화 함수는 신경망의 각 층에서 입력값을 비선형적으로 변환하여, 비선형 문제를 해결할 수 있도록 돕는 역할옵티마이저는 가중치의 업데이트에 포커스를 맞추며, 모델이 최적의 가중치를 찾도록 도와 학습의 성능을 향상- 활성화 함수 예시 : 시그모이드, ReLU, 소프트맥스 등
- 옵티마이저 예시 : SGD, 모멘텀, Adam 등의 알고리즘