[알고리즘] 최단 경로 - 플로이드 워셜 알고리즘

유투브 최단거리 강의를 보고 정리한 글입니다.

---

플로이드 워셜 알고리즘

• 모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산한다.

• 플로이드 워셜 알고리즘은 다익스트라와 마찬가지로 단계별로 거쳐가는 노드를 기준으로 알고리즘 수행
  - 다만 매 단게마다 방문하지 않은 노드 중 최단 거리를 갖는 노드를 찾는 과정이 필요없음

• 플로이드 워셜은 2차원 테이블에 최단 거리 정보 저장

• 플로이드 워셜 알고리즘은 다이나믹 프로그래밍(DP) 유형에 속함

• 노드의 개수가 적은 경우 효과적

• 각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인
  - a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사

• 점화식
  

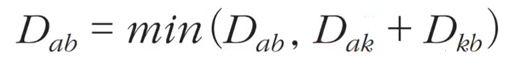
예시

• 초기상태 : 그래프 준비하고 최단거리 테이블 초기화
  초기 간선 상태 저장
  

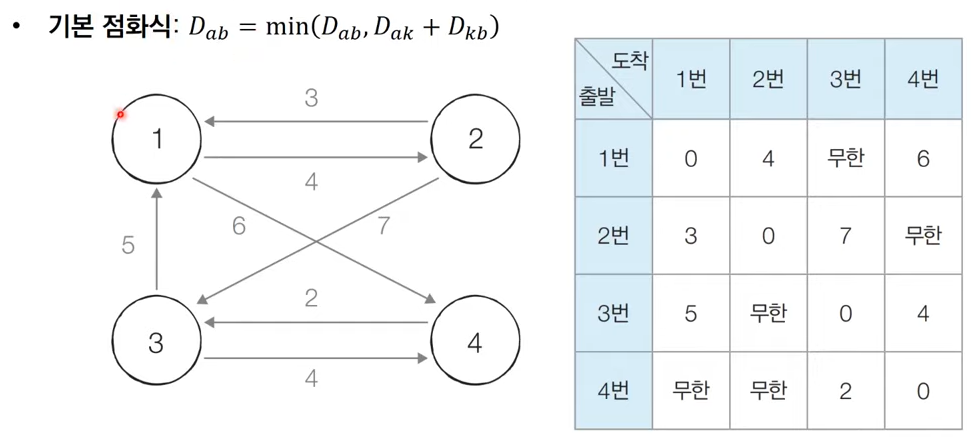
• Step 1 : 1번 노드를 거쳐가는 경우 고려
  

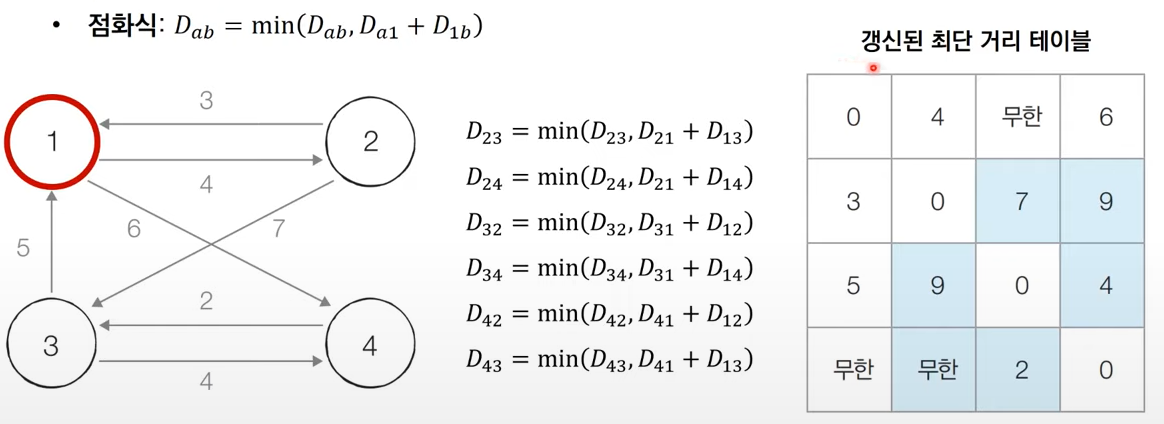
• Step 2 : 2번 노드를 거쳐가는 경우 고려
  

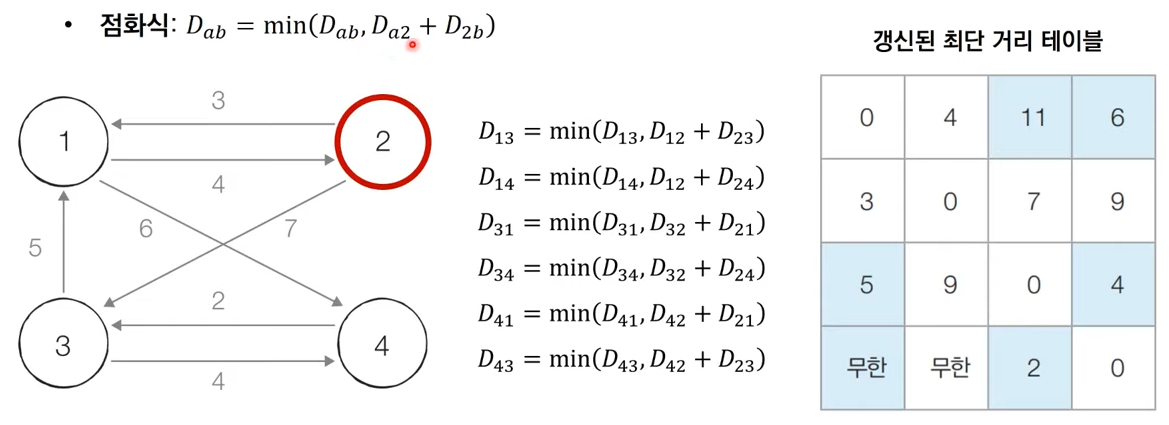
• Step 3 : 3번 노드를 거쳐가는 경우 고려
  

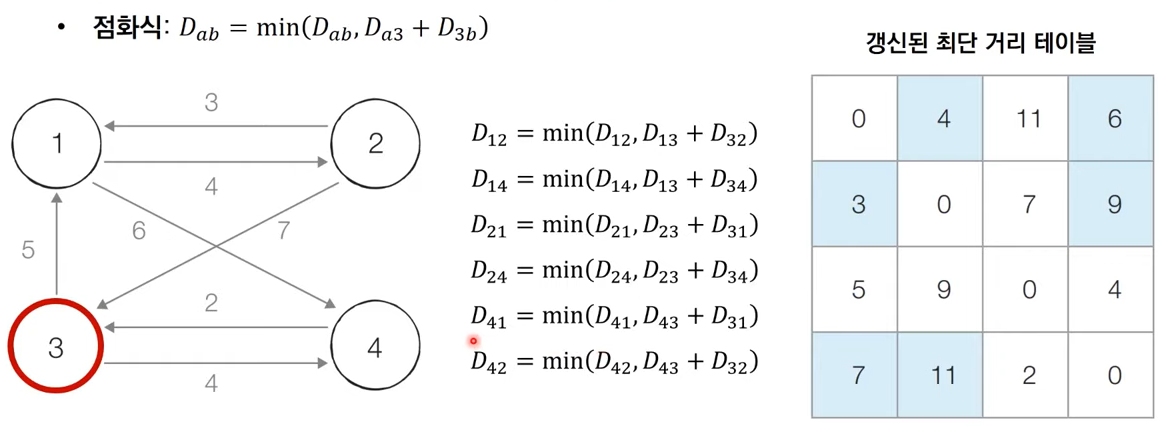
• Step 4 : 4번 노드를 거쳐가는 경우 고려
  

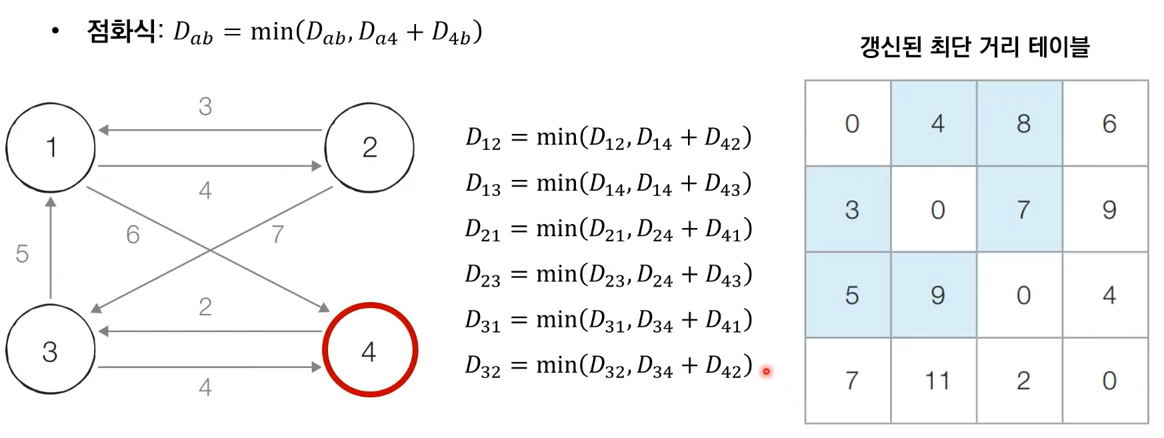
구현

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class floyd_warshall {
    public static final int INF = (int) 1e9;

    //노드의 개수 n 간선의 개수 m
    //노드 개수는 최대 500개 가정

    public static int n, m;

    //2차원 배열(그래프 표현)를 만들기
    public static int[][] graph = new int[501][501];

    public static void solution() throws IOException{
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(bf.readLine());

        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());

        //최단거리 테이블을 모두 무한으로 초기화
        for(int i=0;i<501;i++){
            Arrays.fill(graph[i],INF);
        }

        //자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
        for(int i = 1; i<=n;i++){
            for(int j=1;j<=n;j++){
                if(i==j){
                    graph[i][j] = 0;
                }
            }
        }

        //각 간선에 대한 정보를 입력 받아 그 값으로 초기화
        for(int i=0;i<m;i++){
            //a에서 b로 가는 비용은 c
            st = new StringTokenizer(bf.readLine());
            int a= Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int c= Integer.parseInt(st.nextToken());

            graph[a][b] = c;
        }

        //점화식에 따라 플로이드 워셜 알고리즘 수행
        for(int k=1;k<=n;k++){
            for(int a=1;a<=n;a++){
                for(int b=1;b<=n;b++){
                    graph[a][b] = Math.min(graph[a][b], graph[a][k]+graph[k][b]);
                }
            }
        }

        //수행된 결과 출력
        for(int a =1; a<=n;a++){
            for(int b=1;b<=n;b++){
                //도달할 수 없는경우, 무한 출력
                if(graph[a][b] == INF){
                    System.out.println("Infinity");
                }
                else{
                    System.out.println(a+" "+b+" :"+graph[a][b]);
                }
            }
        }
    }
}

성능 분석

• 노드의 개수가 N개일 떄 알고리즘상으로 B번의 단계 수행
  - 각 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐가는 모든 경로를 고려
• 따라서 총 시간 복잡도 : O(N^3) -> 3중 포문 사용