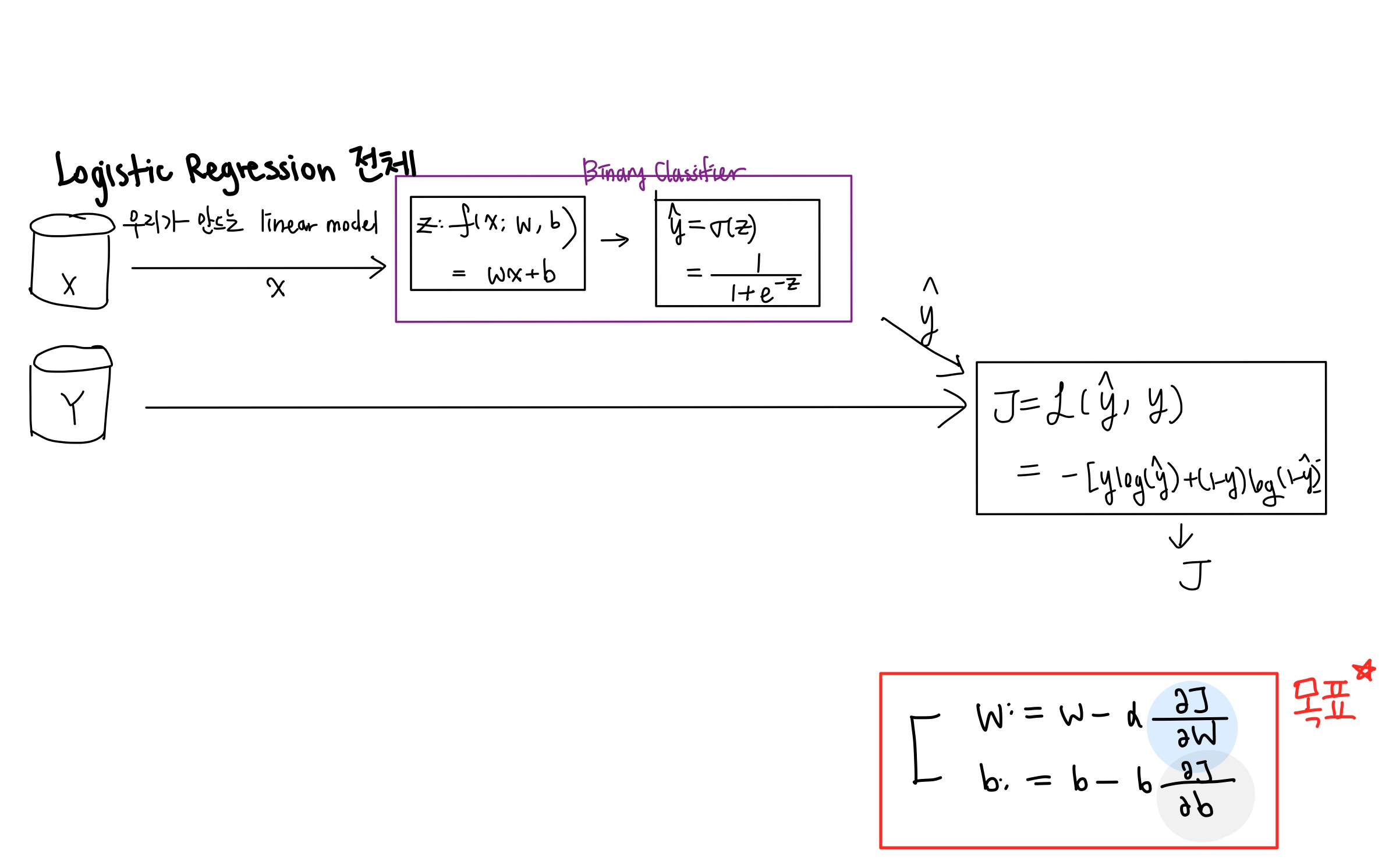
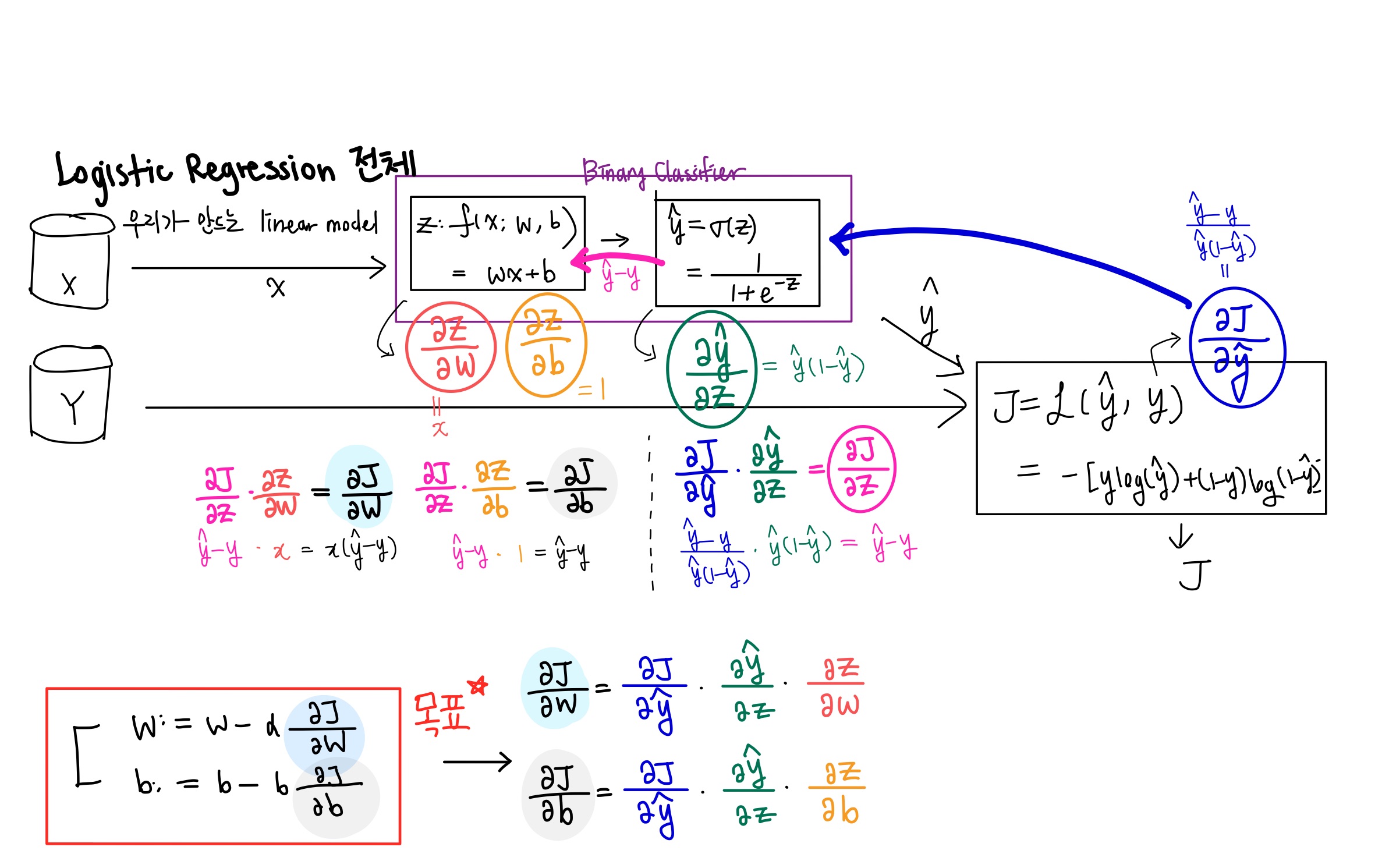
지금까지 배운 내용을 생각해보자.
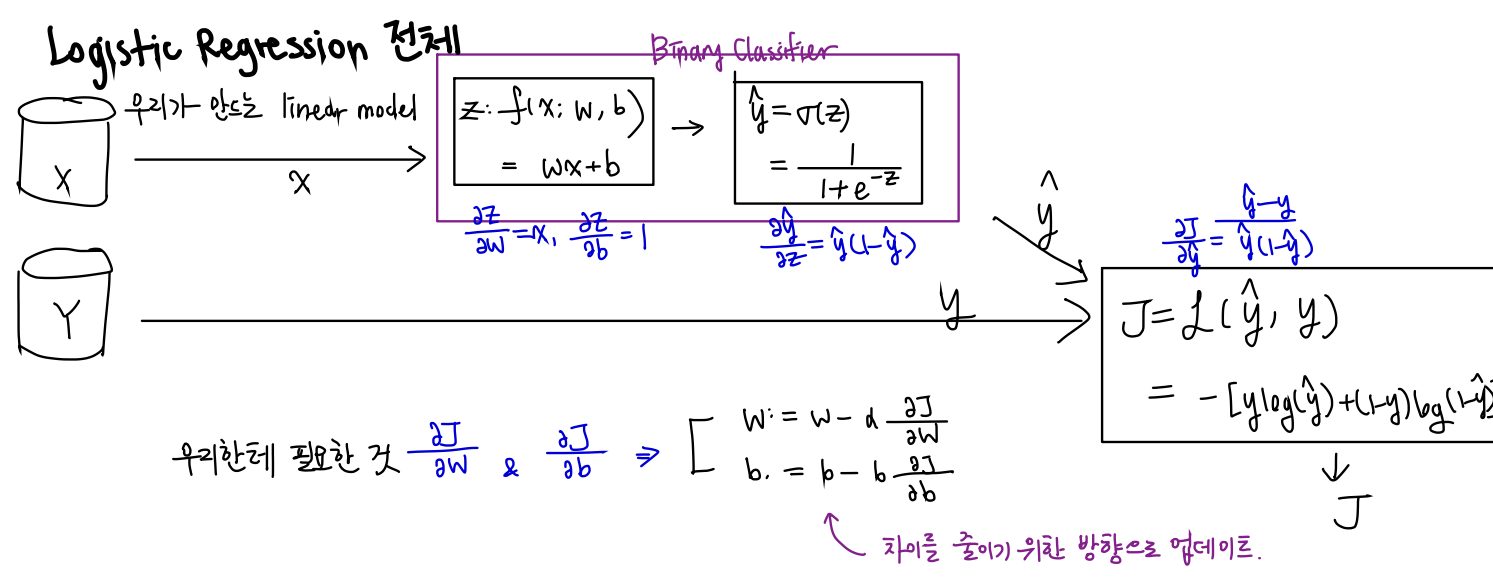
input x를 binary classifier에 집어넣는다. 그리고 손실함수를 구한다음에 손실이 적어질 때까지 학습시킨다.
전체적인 플로우는 이해했다.
그렇다면
어떻게 학습시킬 것인가?
사실, 마지막 단계까지 왔으면, 마지막 Loss함수에 대한 파라미터 w와 b로 미분한 값을 구해야 한다.
왜냐?
우리의 최종 목표는
를 구해서 w와 b를 업데이트 해야 하기 때문!!!
암튼 그래서 , 이 두 친구를 구하기 위해서는 긴 여정을 떠나야 한다.
왜냐면, 일단 J식에는 w,b가 없고 를 구하는 식에도 w,b가 없기 때문에...
아래 식을 보자.
잘 살펴보면
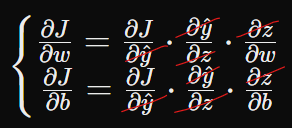
이렇게 지워지는 것을 확인할 수 있다.
모든 식에 대해서 미분값을 구해서 차례차례 곱해나가면 된다.
이 부분을 설명하기가 조금 빡센데, 수식을 들어가기 전에 방금 말한 전체적인 flow를 다시한번 이해해보자.
Backpropagation 이해하기
데이터를 입력받은 후, Binary Classifier안으로 들어가서 1아니면 0의 예측값이 나오고, Loss Function을 구하게 된다.
그렇지만 우리는 여기서 (우측하단) 목표를 잊지 말아야 한다.
파라미터 업데이트 를 위해서는 Loss Function을 파라미터인 w과 b로 미분해줘야 한다.
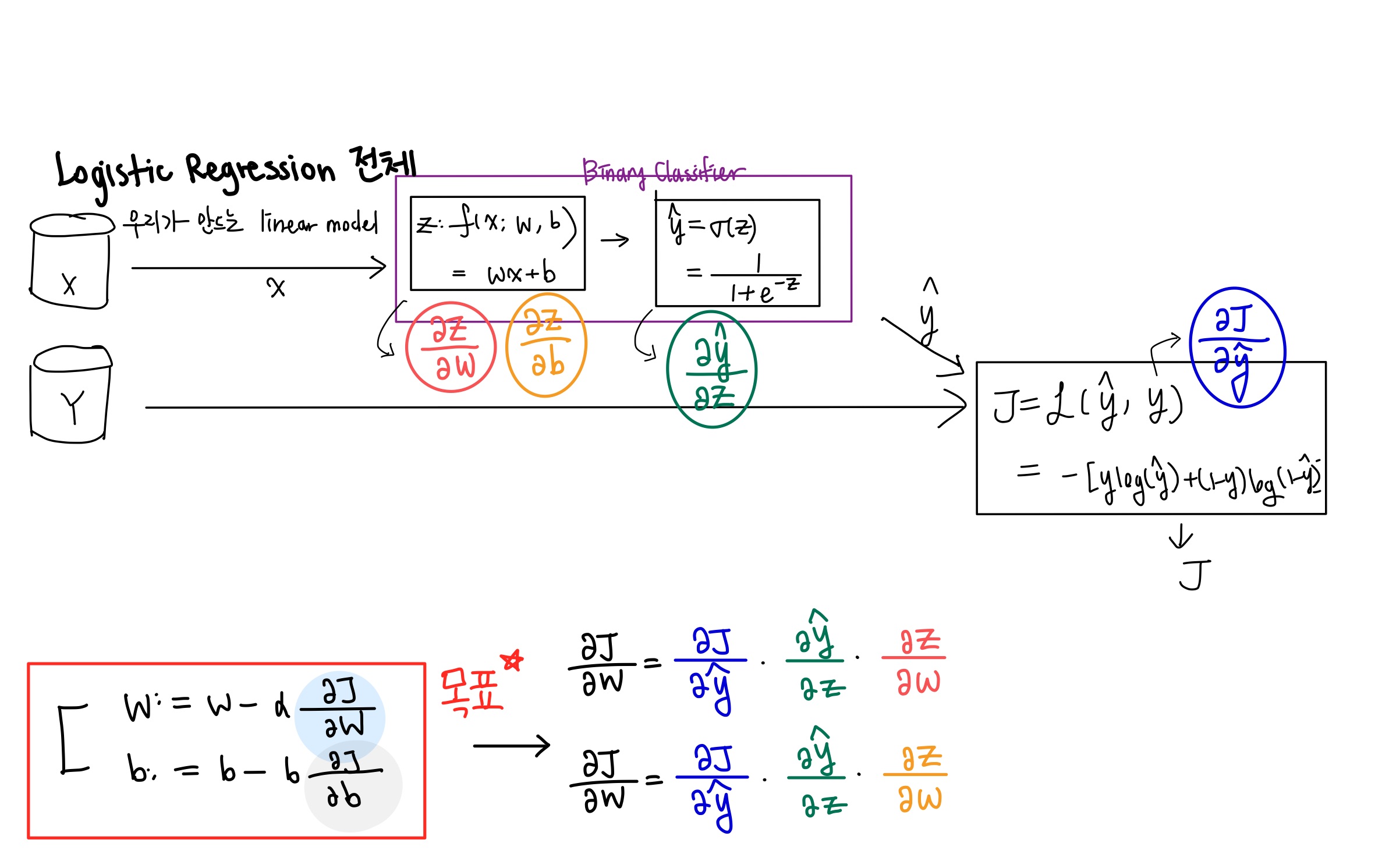
위에서도 언급했듯이 이는 Chain Rule로 가능하다.
아래 사진을 보자.
사진 아래편을 보면 Loss Function을 파라미터인 w과 b로 미분하는 수식을 이렇게 나타낼 수 있다.
각각의 색은 각각의 색 구간에서 미분값을 도출해낼 수 있을 것이다.
구현할때에는 이렇게 한번에 곱할 수가 없기 때문에, 차례대로 곱할 것이다.
처음에는 파란색부터 시작하여, 하나하나씩 Backpropagation을 하면서 곱해나간다.
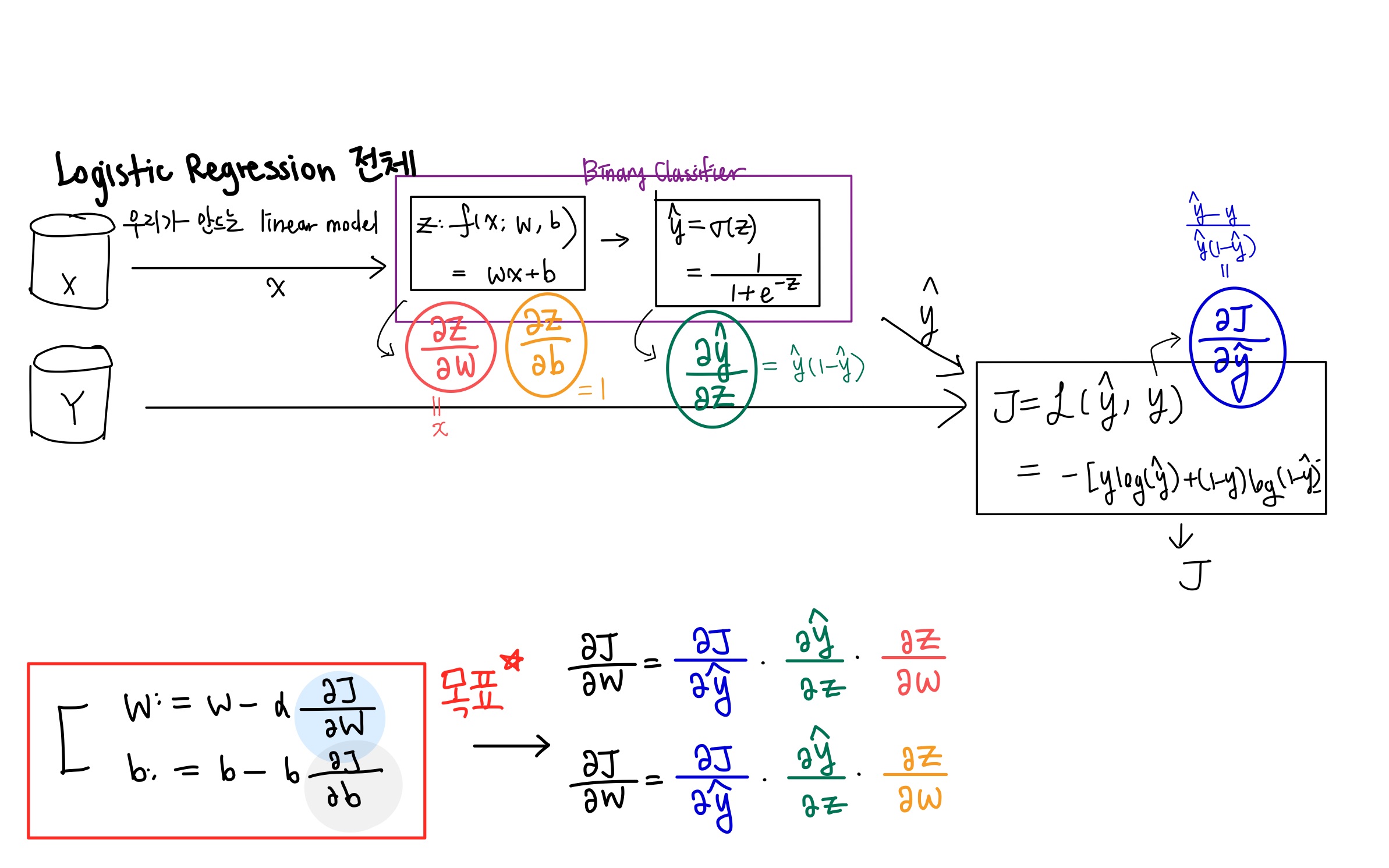
우리가 지금 알 수 있는 미분값을 아래 사진에 적어보았다.
간단하게 각각의 수식을 미분한 값을 적어보았다.
물론 이것들을 한번에 곱할 수 있으면 좋겠지만, 코딩은 flow가 있기 때문에 한번에 곱하지 못한다.
거꾸로 진행한다는 사실을 기억하고 아래 그림을 바로 살펴보자.
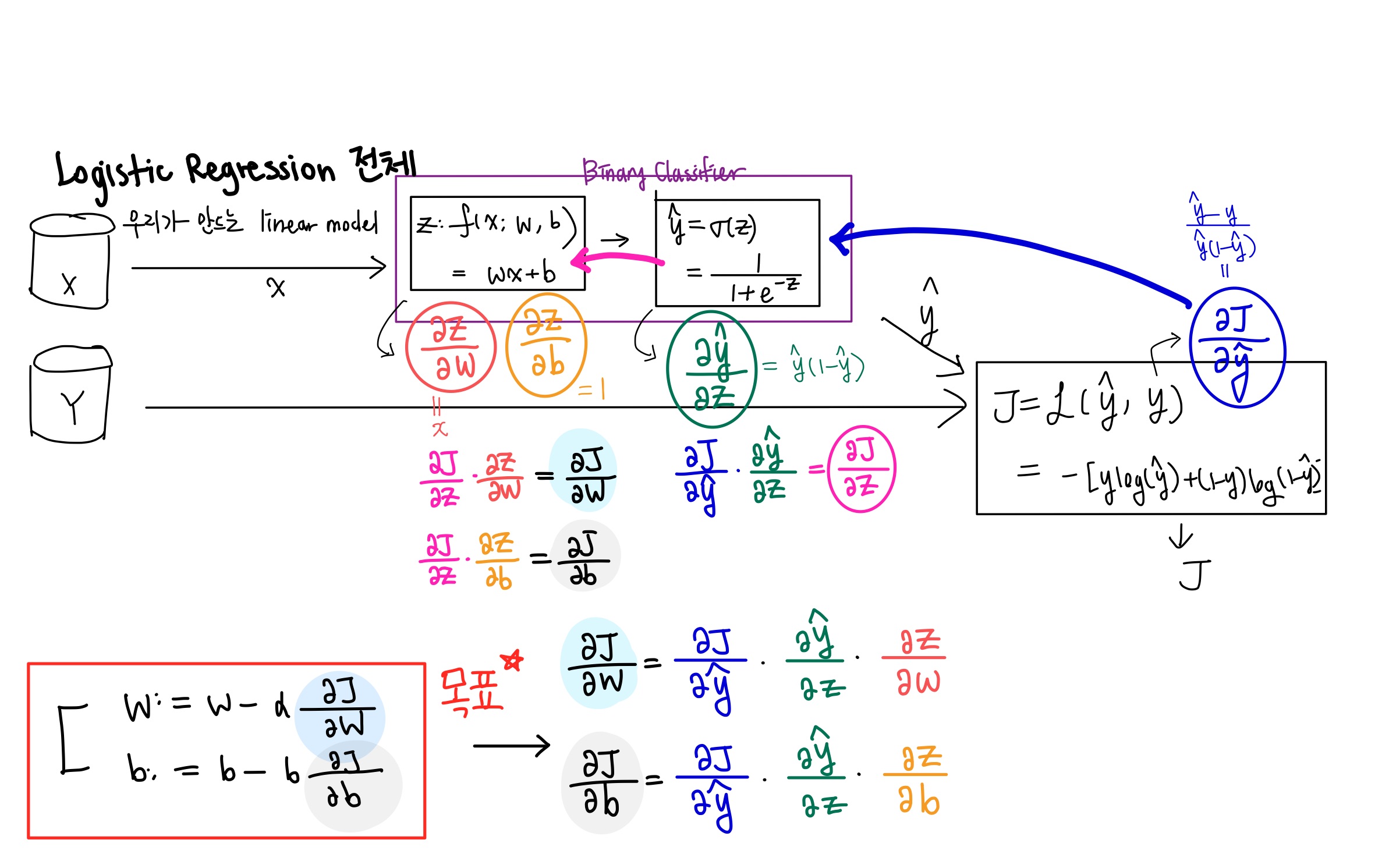
자 조금 복잡해지긴 했지만, 당황하지 말고... 파란색 화살표를 따라가본다.
파란색 수식과 초록색 수식을 곱할 차례이다. 그럼 핑크색 식이 나온다.
핑크색 화살표를 따라가보자. 각각 빨간 수식과 주황 수식을 각각 곱해주면 우리가 원하는 와 를 구할 수 있게 된다.
여기까지 이해하면 전체적인 Flow는 다 이해한 것이다.
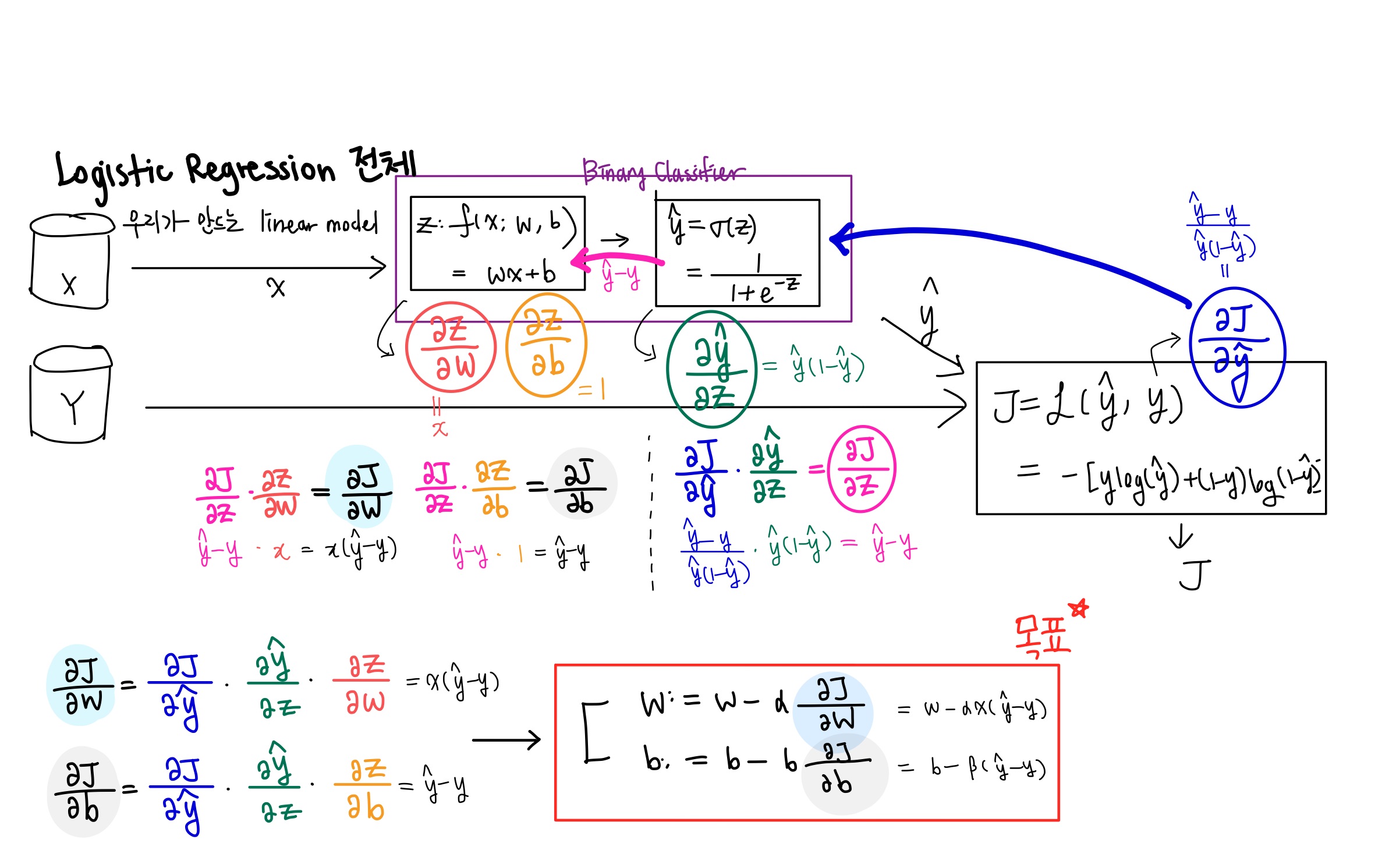
이번에는 정확한 수식을 살펴보자. 헷갈리지 않기 위해 얇은 펜으로 적어보았다.
아래 그림에서 확인하자.
방금 적은 수식을 기반으로 우리가 아까 구해놓았던 미분값들을 대입하였다.
마지막으로 우리가 원하는 w와 b값을 업데이트 하는 식을 구할 수 있다.
아래 그림에서 확인하자.
맨 아래 그림의 위치를 순서대로 바꿨다. 우리의 목표는 오른쪽 빨간색 상자에 있다.
이렇게 우리가 원하는 것을 backpropagation을 통해서 구할 수 있는 방법을 알아보았다.
backpropagation는 간단하게 말하면
내가 전달받은 것 에다가 내 미분을 곱해서 앞쪽으로 전달하는 것
문제점
Backpropagation에서도 발생하는 문제점이 있다.
- Vanishing Gradient
- min-max normalization / standardization
코드 실습
Backpropagation코드실습 이 페이지를 확인하자.
해당 페이지에서 설명은 없기 때문에 위 내용을 완벽히 숙지 후 코드를 하나씩 비교하다보면 정확히 일치할 것이다!