
지난 글에서 Artificial Neuron에 대한 간단한 개요를 작성했었다.
보고 오면 이해하는데 도움이 될 수도 있다.
Artificial Neuron
은 두 가지 함수로 이루어져 있다.
"Affine Function"
↓
"Activation Function"
Affine Function
에서 inputdms 이다.
여기서 x와 w들을 "손에 주렁주렁 달고 다니지 말고 봉투 하나에 담는" 개념으로 벡터로 감싸보자.
지난 글에서도 설명했다시피, 내적이라는 개념을 도입해서 를 구해줄 수 있다.
이렇게 하나 하나씩에 곱해준 후 합을 구해주는 것이다.
간단하게 쓰면 가 되겠다. 물론 b도 있어야 하지만 설명을 위해 제외하고 설명한다.
여기서 와 를 내적한다는 것은 나랑 얼마나 유사한지 확인하는 방법이다.
아래 그림을 보자.
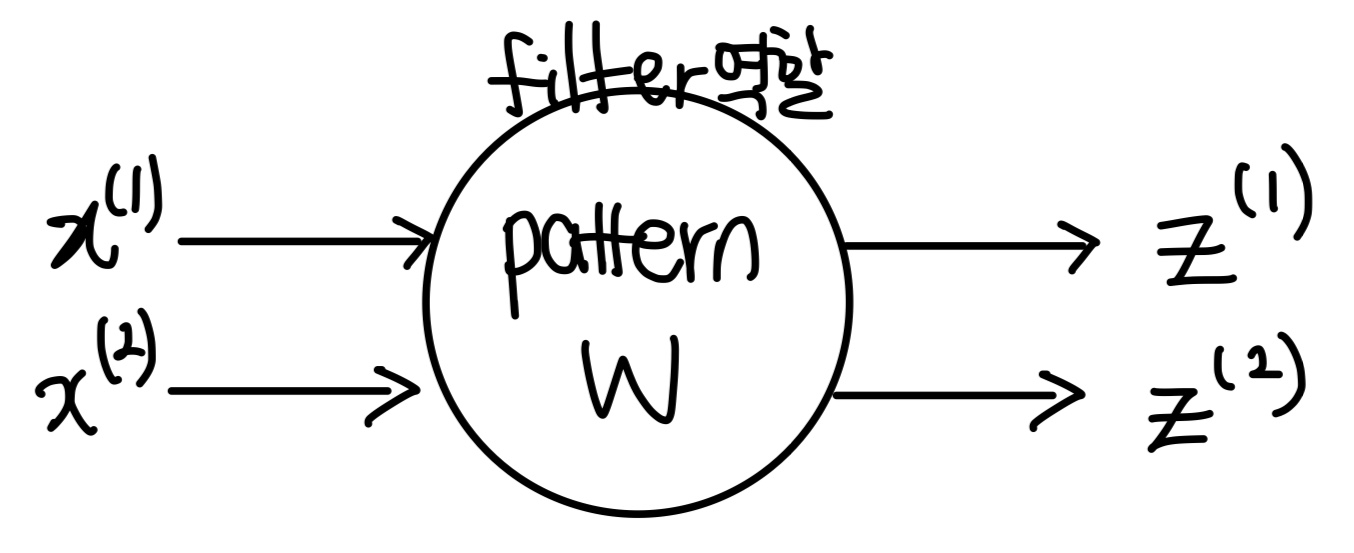
입력x를 받으면 w가 필터 역할을 한다. 그리고 출력값으로 z가 출력된다.
또 다른 말로 Correlation이라고도 한다.
아래 그림을 보자.
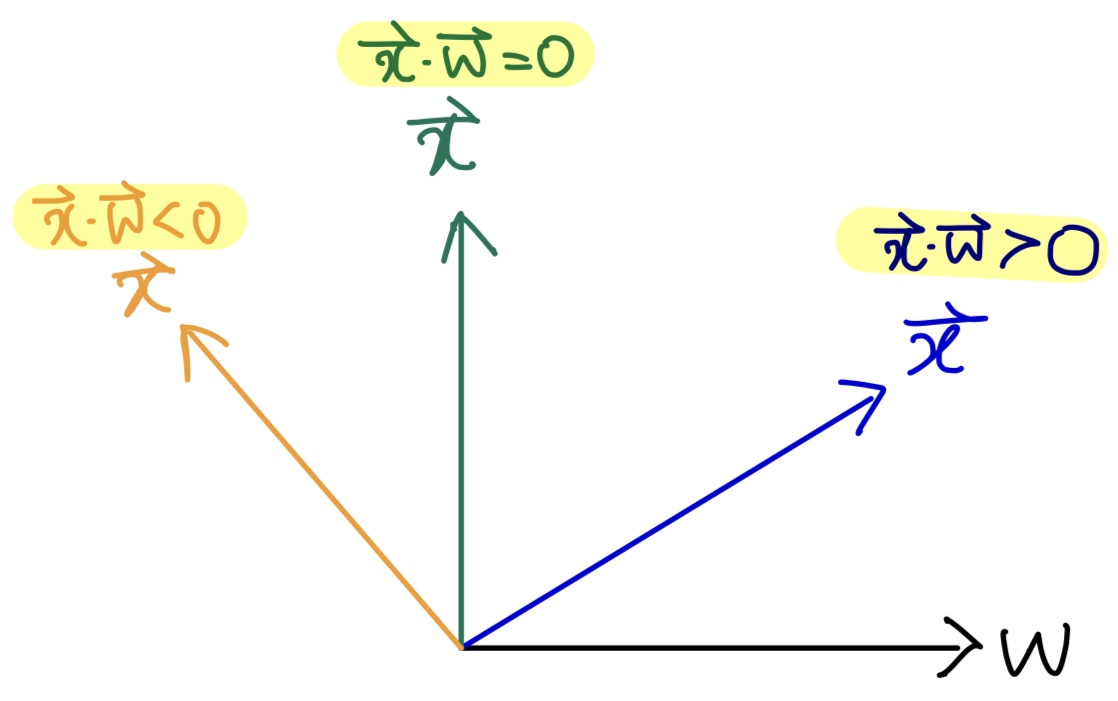
검정색 선 처럼 w값이 있을 때,
파란색 벡터값은 w와 Correlation이 높다. Correlation값이 높다는 것은 을 의미한다.
초록색 벡터값은 w와 수직이므로 이고
주황색 벡터값은 w와 Correlation이 낮다. 전혀 유사하지 않다. 따라서 을 의미한다.
그 다음으로 Activation Function을 살펴보자.
Activation Function
우리가 이전에 배운 Sigmoid로 예시를 들어보려고 한다.
맨 처음에 Artificial Neuron은 Affine Function에서 나온 값을 Activation Function에게 전달해 준다고 했었다.
Affine Function에서
입력된 값을들 가중치와 내적하면서 유사도를 측정한다.
그 다음 Activation Function (Sigmoid)로 넘어와서 전달받은 값을 확률로 바꿔준다.
유사하면 1을 출력하고, 0을 출력한다.
여기서 궁금한 점이 있었는데, "유사하다"는 기준은 누가 정하는 걸까?
- 컴퓨터가 학습하면서 정하는 것이기 때문에 우리가 정확히 무슨 이유로 판단했는지 알기 어렵다.
개념이 이해됐다면, 아까 빼먹었던 bias를 다시 넣어서 전체 식을 완성해보자.
자기가 가지고 있는 w가 x와 비슷하면 출력이 1(Activation이 된다) 아니면 0(Activation이 안된다)
그렇다면 bias가 하는 역할은 뭘까?
여기서 값이 니까 조금만 생각해보면 알 수 있다.
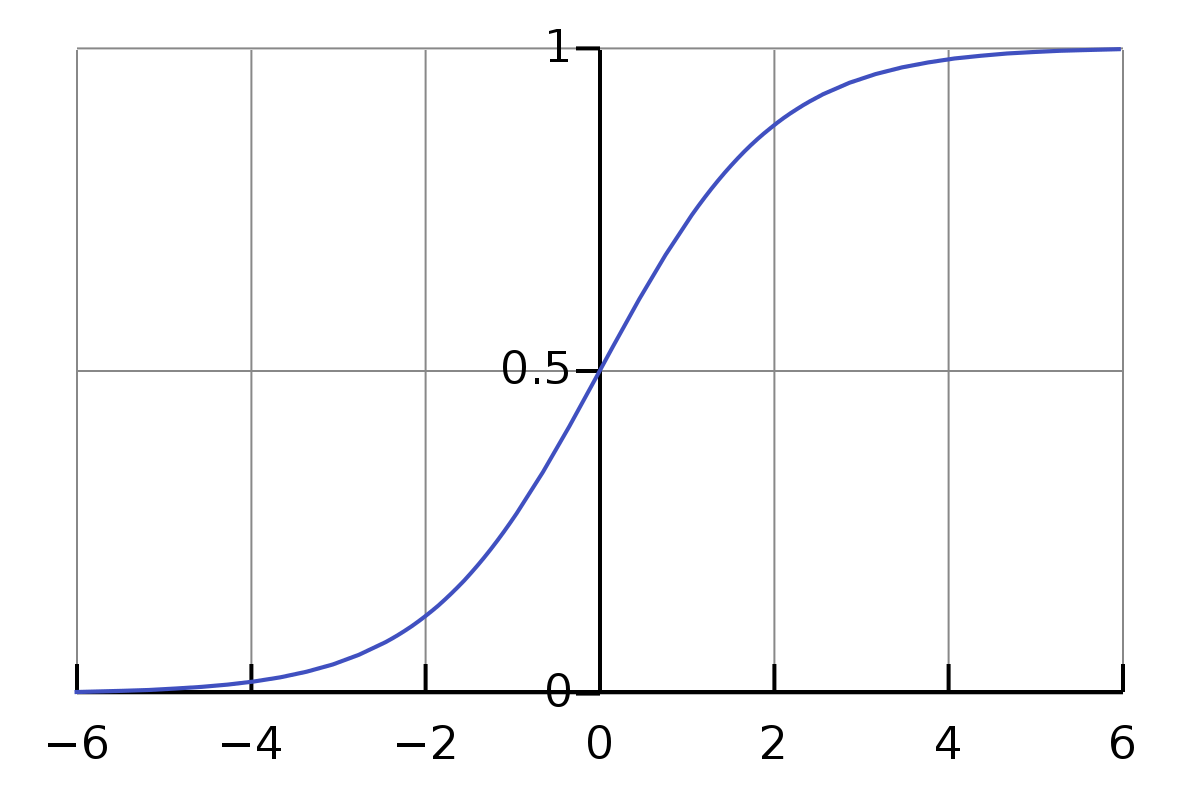
여기서 x축이 이지 않은가? b는 이 점을 위 아래로 이동시킨다.
즉,
만약 b가 양수라면 Activation이 잘 되는 뉴런으로 만들 수 있다.
만약 b가 음수라면 Activation이 잘 되지 않는 뉴런으로 만들 수 있다.
다음 글에서는 Hyperplane에 대해서 알아보자.
