코드 실습
Dataset 만들기
import numpy as np
import matplotlib.pyplot as plt
def make_dataset(n_samples, decision_boundary, direction):
X = np.random.normal(loc=decision_boundary, scale=2,
size=(n_samples, ))
if direction == 'pos':
Y = (X > decision_boundary).astype(int)
elif direction == 'neg':
Y = (X < decision_boundary).astype(int)
return X, Y
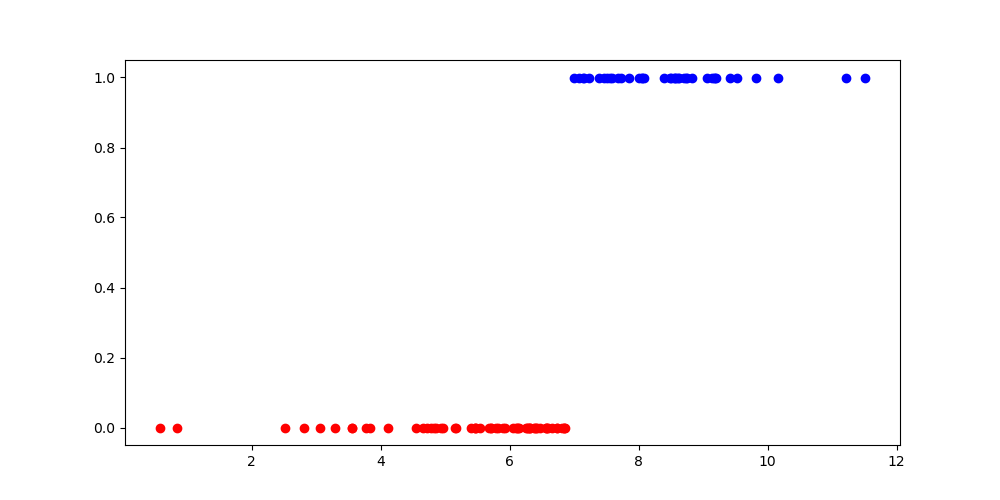
n_samples = 100
decision_boundary = 7
direction = 'pos'
X, Y = make_dataset(n_samples, decision_boundary, direction)
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(X[Y == 0], Y[Y == 0], color='red')
ax.scatter(X[Y == 1], Y[Y == 1], color='blue')
plt.show()결과
Class 구현하기 (forward)
class LinearFunction:
def __init__(self, w=None, b=None):
if w is None: self.w = np.random.normal(0, 1, 1)
else: self.w = w
if b is None: self.b = np.random.normal(0, 1, 1)
else: self.b = b
def __call__(self, x): return self.w * x + self.b
def backward(self): pass
class Sigmoid:
def __call__(self, z):
a = 1 / (1 + np.exp(-z))
return a
def backward(self): pass
class BCELoss:
def __call__(self, pred, y):
self.pred, self.y = pred, y
loss = -(y * np.log(pred) + (1 - y) * np.log(1 - pred))
return loss
def backward(self): pass학습 세팅하기
import numpy as np
import matplotlib.pyplot as plt
def make_dataset(n_samples, decision_boundary, direction):
X = np.random.normal(loc=decision_boundary, scale=2,
size=(n_samples, ))
if direction == 'pos':
Y = (X > decision_boundary).astype(int)
elif direction == 'neg':
Y = (X < decision_boundary).astype(int)
return X, Y
class LinearFunction:
def __init__(self, w=None, b=None):
if w is None: self.w = np.random.normal(0, 1, 1)
else: self.w = w
if b is None: self.b = np.random.normal(0, 1, 1)
else: self.b = b
def __call__(self, x): return self.w * x + self.b
def backward(self): pass
class Sigmoid:
def __call__(self, z):
a = 1 / (1 + np.exp(-z))
return a
def backward(self): pass
class BCELoss:
def __call__(self, pred, y):
self.pred, self.y = pred, y
loss = -(y * np.log(pred) + (1 - y) * np.log(1 - pred))
return loss
def backward(self): pass
n_samples = 100
decision_boundary = 7
direction = 'pos'
X, Y = make_dataset(n_samples, decision_boundary, direction)
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(X[Y == 0], Y[Y == 0], color='red')
ax.scatter(X[Y == 1], Y[Y == 1], color='blue')
# 필요한 object 만들기
linear_function = LinearFunction()
sigmoid = Sigmoid()
loss_fn = BCELoss()
# 초기 모델 시각화하기
xlim = ax.get_xlim()
function_x = np.linspace(xlim[0], xlim[1], 100)
function_y = sigmoid(linear_function(function_x))
ax.plot(function_x, function_y)
plt.show()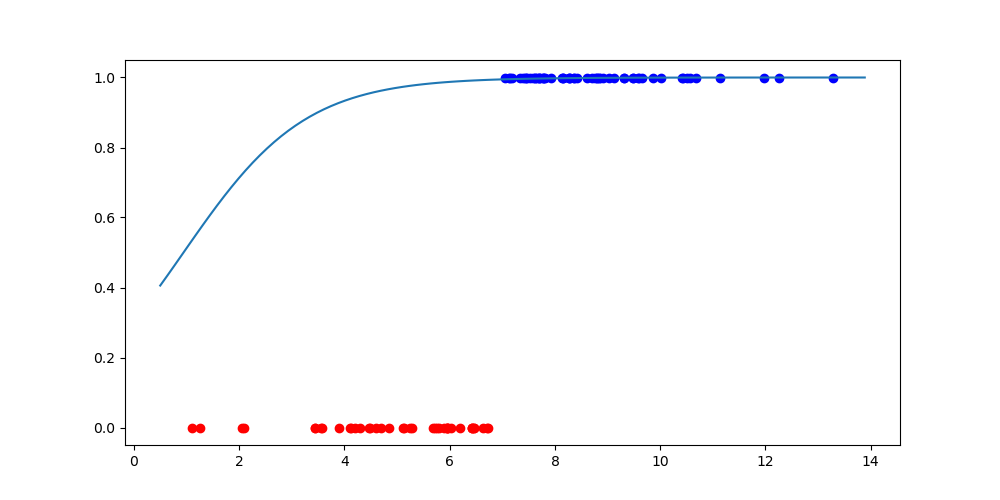
forward만 실행
for x, y in zip(X, Y):
z = linear_function(x)
pred = sigmoid(z)
loss = loss_fn(pred, y)
print(loss)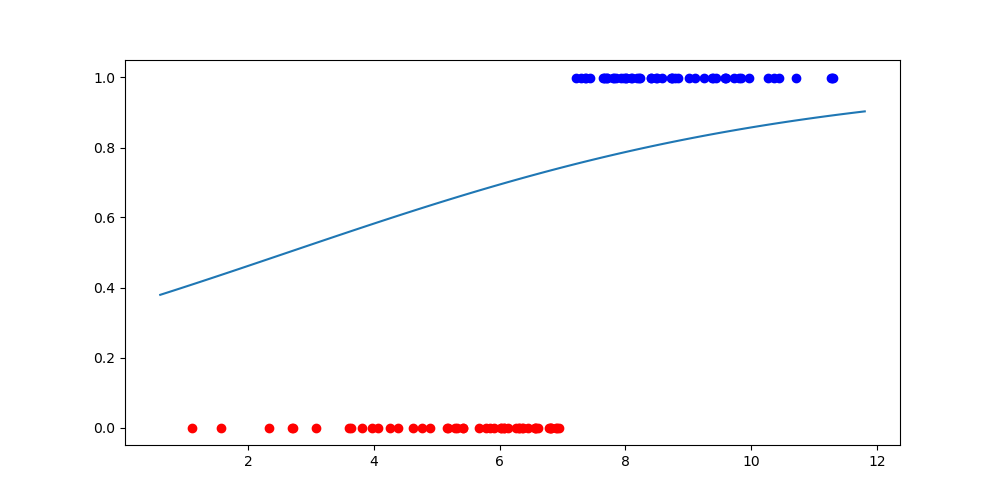
class 구현하기 (backward)
class LinearFunction:
def __init__(self, w=None, b=None):
if w is None: self.w = np.random.normal(0, 1, 1)
else: self.w = w
if b is None: self.b = np.random.normal(0, 1, 1)
else: self.b = b
def __call__(self, x):
self.x = x
return self.w * x + self.b
def backward(self, dloss_dz, lr):
dz_dw = self.x
dz_db = 1
dloss_dw = dloss_dz * dz_dw
dloss_db = dloss_dz * dz_db
self.w = self.w - lr * dloss_dw
self.b = self.b - lr * dloss_db
class Sigmoid:
def __call__(self, z):
self.a = 1 / (1 + np.exp(-z))
return self.a
def backward(self, dloss_da):
da_dz = self.a * (1 - self.a)
dloss_dz = dloss_da * da_dz
return dloss_dz
class BCELoss:
def __call__(self, pred, y):
self.pred, self.y = pred, y
loss = -(y * np.log(pred) + (1 - y) * np.log(1 - pred))
return loss
def backward(self):
dloss_dpred = (self.pred - self.y) / (self.pred * (1 - self.pred))
return dloss_dpred학습 loop 만들기
for _ in range(10):
for x, y in zip(X, Y):
# forward propagation
z = linear_function(x)
pred = sigmoid(z)
loss = loss_fn(pred, y)
# backward propagation
dloss_dpred = loss_fn.backward()
dloss_dz = sigmoid.backward(dloss_dpred)
linear_function.backward(dloss_dz, lr=0.01)
# visualization
function_y = sigmoid(linear_function(function_x))
ax.plot(function_x, function_y, color='skyblue')
function_y = sigmoid(linear_function(function_x))
ax.plot(function_x, function_y, color='red')
plt.show()전체 코드
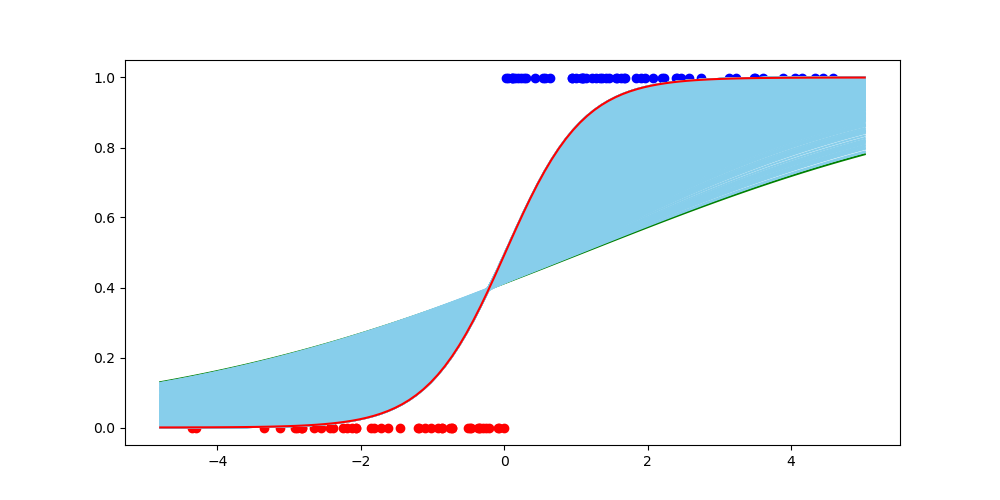
import numpy as np
import matplotlib.pyplot as plt
def make_dataset(n_samples, decision_boundary, direction):
X = np.random.normal(loc=decision_boundary, scale=2,
size=(n_samples, ))
if direction == 'pos':
Y = (X > decision_boundary).astype(int)
elif direction == 'neg':
Y = (X < decision_boundary).astype(int)
return X, Y
class LinearFunction:
def __init__(self, w=None, b=None):
if w is None: self.w = np.random.normal(0, 1, 1)
else: self.w = w
if b is None: self.b = np.random.normal(0, 1, 1)
else: self.b = b
def __call__(self, x):
self.x = x
return self.w * x + self.b
def backward(self, dloss_dz, lr):
dz_dw = self.x
dz_db = 1
dloss_dw = dloss_dz * dz_dw
dloss_db = dloss_dz * dz_db
self.w = self.w - lr * dloss_dw
self.b = self.b - lr * dloss_db
class Sigmoid:
def __call__(self, z):
self.a = 1 / (1 + np.exp(-z))
return self.a
def backward(self, dloss_da):
da_dz = self.a * (1 - self.a)
dloss_dz = dloss_da * da_dz
return dloss_dz
class BCELoss:
def __call__(self, pred, y):
self.pred, self.y = pred, y
loss = -(y * np.log(pred) + (1 - y) * np.log(1 - pred))
return loss
def backward(self):
dloss_dpred = (self.pred - self.y) / (self.pred * (1 - self.pred))
return dloss_dpred
n_samples = 100
decision_boundary = 0
direction = 'pos'
X, Y = make_dataset(n_samples, decision_boundary, direction)
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(X[Y == 0], Y[Y == 0], color='red')
ax.scatter(X[Y == 1], Y[Y == 1], color='blue')
# 필요한 object 만들기
linear_function = LinearFunction()
sigmoid = Sigmoid()
loss_fn = BCELoss()
# 초기 모델 시각화하기
xlim = ax.get_xlim()
function_x = np.linspace(xlim[0], xlim[1], 100)
function_y = sigmoid(linear_function(function_x))
ax.plot(function_x, function_y, color='green')
for _ in range(10):
for x, y in zip(X, Y):
# forward propagation
z = linear_function(x)
pred = sigmoid(z)
loss = loss_fn(pred, y)
# backward propagation
dloss_dpred = loss_fn.backward()
dloss_dz = sigmoid.backward(dloss_dpred)
linear_function.backward(dloss_dz, lr=0.01)
# visualization
function_y = sigmoid(linear_function(function_x))
ax.plot(function_x, function_y, color='skyblue')
function_y = sigmoid(linear_function(function_x))
ax.plot(function_x, function_y, color='red')
plt.show()