
저번 시간에는 를 따르는 것 처럼 보이는 dataset을 만들고, 이에 따라 를 만드는 모델을 만들었다.
어떻게? gradient based learning 을 이용해서 loss를 최소화하는 방향의 gradient로 a,b를 업데이트하고 loss 는 squared error로 구했다.
병렬연산
GPU
GPU는 CPU보다 성능이 떨어자는 CORE를 무수히 많이 갖고 있다.
연산을 병렬적으로 하는데, 예를 들어 행렬의 덧셈, Haradmard product, Fourier transform같은 것들을 할 수 있다.
반면에 CPU는 한번에 하나의 연산을 한다.
DL에서의 병렬연산
지난 시간에서 실습했던 코드와 달리, 한 번에 하나의 데이터쌍을 학습하지 않고 한번에 여러개의 데이터(mini batch)를 사용한다.
예를 들어, 데이터셋의 100개의 샘플이 있다면 한번에 8, 16, 32개를 학습한다.
Linear Regression 중의 병렬연산
우리가 살펴봤던 것은, 한 번의 학습 데이터에 하나의 샘플 (x,y)를 사용했다면
이제는 한 번의 학습을 위해 모든 데이터셋을 사용한다. (극단적으로 말하자면)
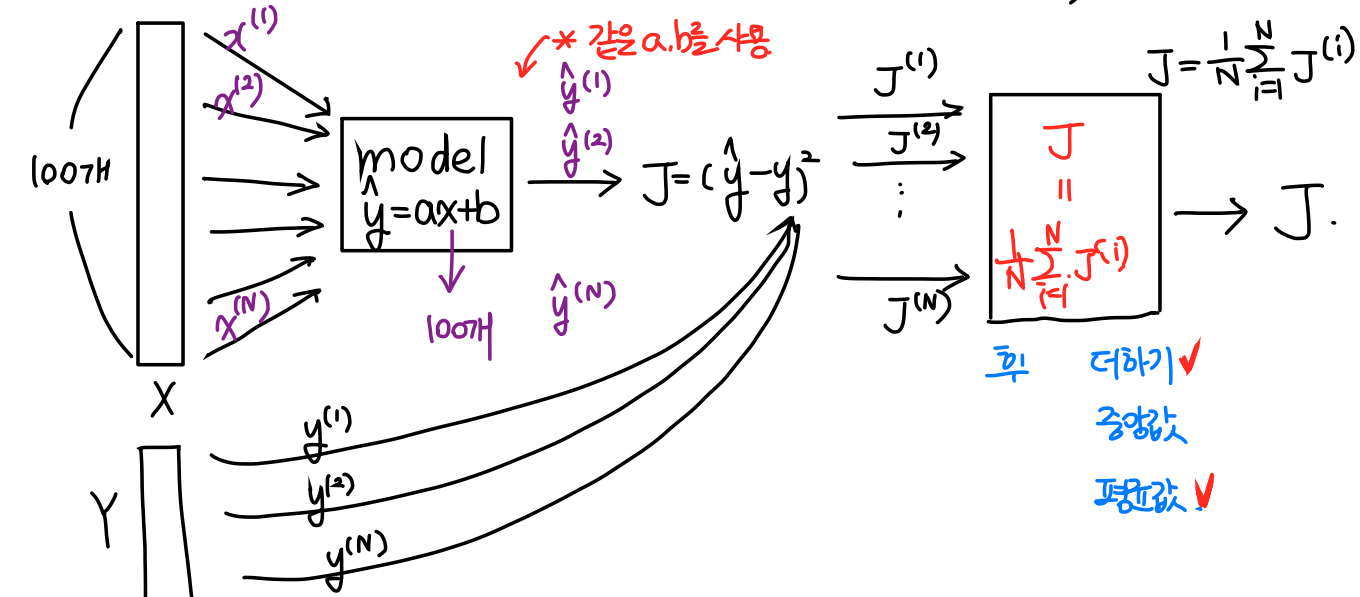
위 그림에서 보면 100개의 x값을 모델 안에 한번에 (병렬연산) 집어넣는다. 한번에 넣기 떄문에 같은 a,b값을 사용하게 된다.
예측값인 이 100개가 출력된다.
여기서 그럼 라는 오차가 100개가 출력되겠죠?
이제 이 100개를 어떻게 하나로 합치느냐의 문제로 넘어온다.
1. 다 더한다.✅
2. 중앙값으로 정한다.
3. 평균값으로 정한다.✅
보통 1번과 3번으로 하는데 3번으로 많이 한다. 하지만 이 문제 역시 자신이 쓰는 데이터에 대해서 다르게 처리할 수 있어야 한다.
3번. 평균값으로 정하기 위해서 아래와 같은 수식을 사용한다.
이것이 우리가 알고 있는 Mean Squared Error(MSE) 이다.
이렇게 Loss값들의 평균을 구할 때 update는 어떻게 이루어지는지 자세히 살펴보자.
Loss들의 평균을 구할 때 update에서 벌어지는 일
위에 식을 이해했다면 아래는 금방 이해할 수 있을 것이다.
그냥 한 발자국 뒤로 돌아간 것이다.
는 이기 떄문에! 이렇게 나올 수 있다.
그렇다면 위 식에서 loss를 줄이기 위해서는 어떻게 해야 할까?
미분한다.
위 식을 전개해보자.
맨 마지막에 이 부분이 미분되면서 가 되었다는 사실을 주의하자.
나머지는 어려운 수식은 아니다.
여기서 마지막 결과부분의 수식을 살펴보면,
i번째 데이터 와 를 사용했을 때, a의 대한 미분계수
임을 확인할 수 있다.
즉,
인 셈이다.
n번째 데이터를 넣었을 때, a가 어떻게 학습되어야 하는지 보여준다.
그래프로 설명해보면,
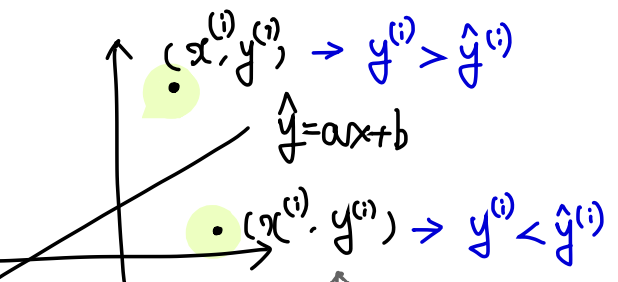
검정 직선을 지나는 선이 있고, 위 아래로 데이터가 있다고 하자.
이 두 점은 데이터로써 학습을 하면서 중간의 검은색 직선을 자기쪽으로 잡아당긴다.
왜냐면 학습 => 전체 데이터를 반영하는 직선이 모든 점을 지나는게 목표이기 때문!
데이터 하나는 오로지 함수가 자기를 예측하는 방향으로 parameter를 이동시킨다.
어떻게 보면 이기적이라고 생각할 수 있겠다.
그래서 모든 점들을 반영하기 위해서는 함수가 아마 이렇게 외칠 것이다.
"난 평균을 반영하겠어!"
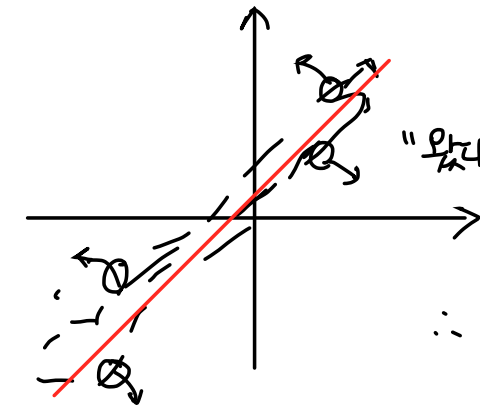
이렇게 잡아당기는 데이터들 사이에서 평균을 자리잡으면 전체적인 데이터를 반영하는 함수가 된다.
이렇게 a값을 업데이트 할 수 있다. 수식으로 적어보자.
저번 시간에는 이런 식을 배웠는데 이 식에 이어서 전개해보자.
이렇게 업데이트 할 수 있겠다.
다시 정리하자면,
Loss를 평균낸다 = Loss들의 update영향력도 평균낸다 => 일반화된 방향으로 update가 가능
데이터 하나만 썼을 때 parameter의 변화와 데이터 여러개를 한번에 썼을 때를 비교해보면
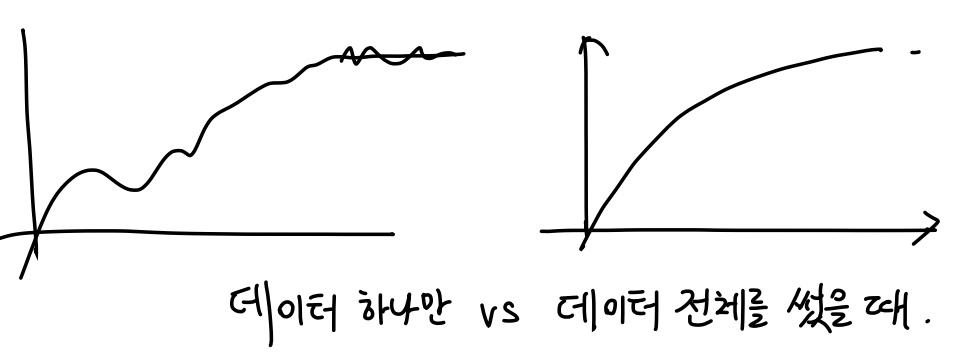
대충 그리긴 했지만, 훨씬 더 안정감을 갖는다.
Logits
Odds
Odds란 확률을 표현하는 다른 표현법이다.
예를 들어, 파란색 공 5개, 빨간색 공 5개가 있다고 하자.
여기서 파란색 공이 뽑힐 odds는 = 파란색 공이 뽑힐 확률 / 빨간색 공이 뽑힐 확률,
빨간색 공이 뽑힐 odds는 = 빨간색 공이 뽑힐 확률 / 파란색 공이 뽑힐 확률이다.
내가 원하는 사건의 확률 / 다른 사건의 확률
odds를 쓰는 이유는 내가 원하는 사건이 일어나는 정도를 느낌적으로 알기 쉽다.
특징
- odds는 항상 양수이다.
- 내가 이길 확률 = 질 확률이면, 이길 odds는 1이다.
- 내가 이길 확률 > 질 확률이면, 이길 odds는 >1이다.
- 내가 이길 확률 < 질 확률이면, 0 < 이길 odds < 1이다.
- 확률이 서로 같을 때를 기준으로 비대칭이다.
여기서 odds에 로그를 씌우면 Logit이 된다.
Logit
로그를 씌웠을 때,
- 그래프는 이런 꼴이 나온다.
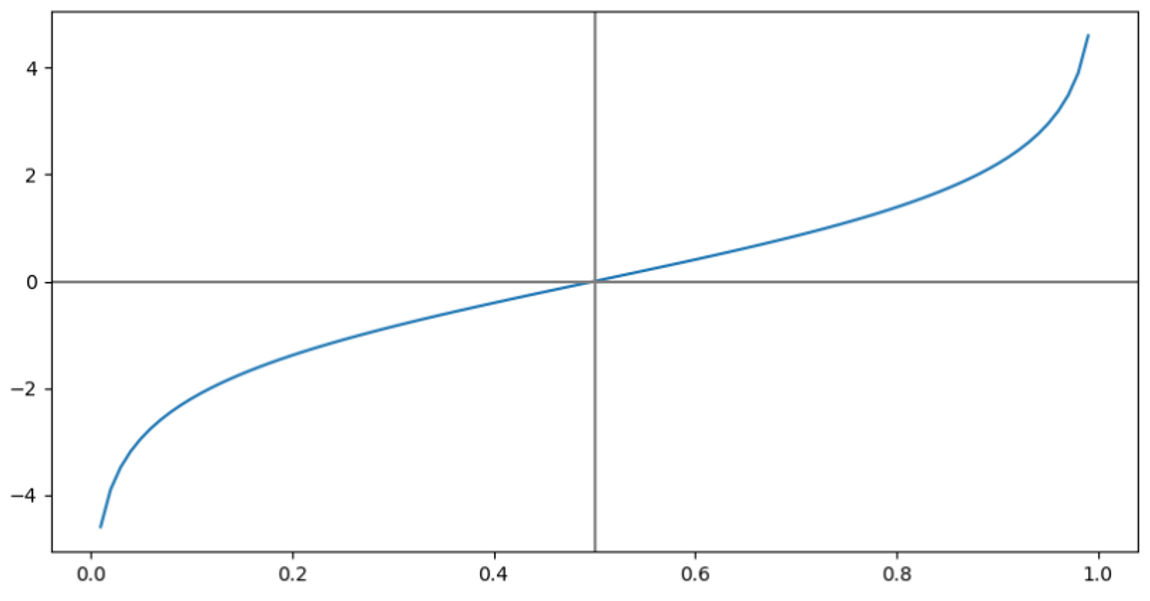
Logit 함수의 특징
- domain = (0, 1) → 확률이기 때문에
- range =
- 기준으로 대칭
Sigmoid Function
위에서 소개한 logit함수를 자세히 살펴보자.
는 이렇게 쓸 수 있다.
위 아래를 뒤집어보자.
맨 아래 식에서 은 입력(logit)이고 는 출력(probability)임을 잊지말자.
즉, logit 함수의 입출력을 반대로 해석하면
sigmoid는 logit을 입력받아 probability로 바꿔주는 함수
Sigmoid의 변환
-
sigmoid 를 x축 방향으로 b만큼 평행이동( ) 한 식을 구하면
-
sigmoid 를 y축 방향으로 a만큼 평행이동( ) 한 식을 구하면
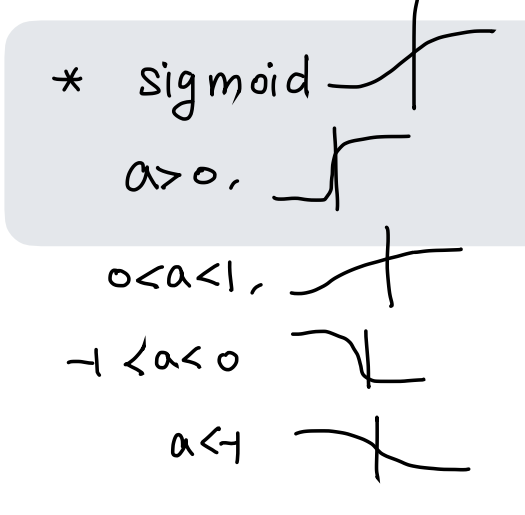
또한 a값에 따라 수축하기도 , 팽창하기도 , y축에 대칭하기도 한다.
합쳐보자.
- sigmoid를 x축 방향으로 수축/팽창시킨 후, x축으로 평행이동 한 식을 구하면어렵지 않게 구할 수 있을 것이다.
여기서 중요한 부분은 의 계수인 는 결국 의 꼴이라는 것.
Binary Classifier로서의 Sigmoid
Binary Classifier는 출력이 0또는 1인 함수이다.
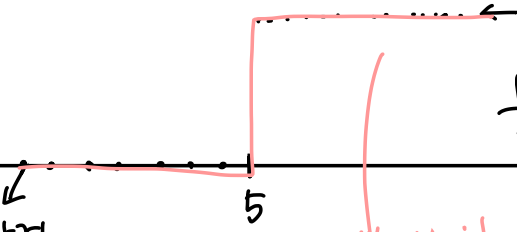
이렇게 계단처럼 생긴 함수를 unit step function이라고 한다.
위 그래프에서는 아래와 같은 함수식이 정의될 수 있겠다.
General Sigmoid Classifier Model
이전에 설명했던 Linear regression model 인 를 떠올려보자.
여기서 출력을 대신 로, 를 sigmoid로 받는다.
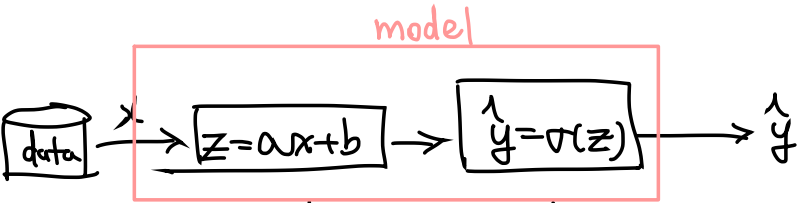
위와 같이 처리할 수 있다.
수식으로 따라가보자.
왜 굳이 linear Regression에 sigmoid를 합쳤을까?
위에 전개된 식을 조금만 변형해보자.
맨 마지막 식을 보면 어딘가 익숙하지 않은가?
바로 일반적인 sigmoid의 꼴에서 x를 ax만큼 이동하고 만큼 이동한 값이다!
Parametric Model 로서의 sigmoid
여기서 a,b가 trainable parameter이다.
a,b를 조절해주면 데이터를 잘 분류하는 함수를 만들 수 있게 된다.!
이 함수는 어떤 output을 갖는지 살펴보자.
Sigmoid Classifier의 Output
- 분류를 할 땐
-
면
-
면
경계점이 생기는 게 보이는가? 그것이 바로 아래에 나오는 내용이다.
-
Sigmoid의 Decision Boundary
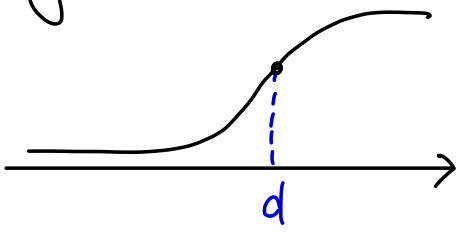
여기에서 sigmoid의 출력이 0.5가 되는 x를 d라 하자.
그럼 좌표 를 decision boundary(결정 경계)라고 하고 이것은 분류이 기준이 된다.
위에서 d를 수치화 할 수 있었다.
원래 함수는 를 지났지만,
위 수식에서 평행이동한 함수는 x축으로 만큼 이동했으므로 을 지나게 된다.
따라서 가 된다.
코드 실습
Sigmoid의 함수 그래프 그리기
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-8, 8, 100)
sigmoid = 1/(1 + np.exp(-x))
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, sigmoid)
ax.scatter(0, 0.5, color='red')
ax.axhline(y=0, color='gray')
ax.axvline(x=0, color='gray')
plt.show()다음 함수의 그래프 그리기
- decision point 도 점으로 표시하기
- 를 바꿔가면서 이론적으로 학습한 것과 일치하는지 분석해보기
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x, a, b):
y = 1/(1 + np.exp(-(a*x + b)))
return y
def get_decision_point(a, b):
x = -b/a
return x, 0.5
a, b = 1, -2
x = np.linspace(-8, 8, 100)
y = sigmoid(x, a, b)
decision_point = get_decision_point(a, b)
fig, ax = plt.subplots(figsize=(10, 5))
ax.plot(x, y)
ax.scatter(decision_point[0], decision_point[1],
color='red')
ax.text(decision_point[0], decision_point[1],
f"({decision_point[0]:.3f}, {decision_point[1]:.3f})",
color='red', fontsize=15)
ax.axhline(y=0, color='gray')
ax.axvline(x=0, color='gray')
plt.show()Binary Classification을 위한 Dataset만들기
- parameter
- decision_point: 얼마를 기준으로 1, 0을 나눌 것인가
- direction: ‘pos’ or ‘neg’
- direction==’pos’: decision point보다 클 때 1, 작으면 0
- direction==’neg’: decision point보다 클 때 0, 작으면 1
- return X, Y
- X: float
- Y: int {0, 1}
- 시각화하기
import numpy as np
import matplotlib.pyplot as plt
def make_dataset(n_samples, decision_boundary, direction):
X = np.random.normal(loc=decision_boundary, scale=2,
size=(n_samples, ))
if direction == 'pos':
Y = (X > decision_boundary).astype(int)
elif direction == 'neg':
Y = (X < decision_boundary).astype(int)
return X, Y
n_samples = 100
decision_boundary = 3
direction = 'neg'
X, Y = make_dataset(n_samples, decision_boundary, direction)
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(X, Y, alpha=0.5)
ax.tick_params(labelsize=15)
plt.show()Dataset을 분류하는 Sigmoid Classifier
- 앞에서 만든 dataset을 잘 분류하는 classifier 만들기
- 데이터셋 그리기
- decision_boundary=3, direction=’pos’
- decision_boundary=1, direction=’neg’
- decision_boundary=5, direction=’pos’
- decision_boundary=-2, direction=’neg’
- decision_boundary=-1, direction=’pos’
- decision_boundary=7, direction=’neg’
- 이 데이터셋을 잘 분류하도록 a, b를 정해서 sigmoid를 데이터셋 그림 위해 곂쳐서 그리기
- 잘 분류하는지 확인해보기(decision point)
import numpy as np
import matplotlib.pyplot as plt
# Sigmoid 함수
def sigmoid(x, a=1, b=0):
return 1 / (1 + np.exp(-a * (x - b)))
# 데이터셋
decision_boundaries = [3, 1, 5, -2, -1, 7]
directions = ['pos', 'neg', 'pos', 'neg', 'pos', 'neg']
Y = [1 if direction == 'pos' else 0 for direction in directions]
# 파라미터 설정
a = 1
b = np.mean(decision_boundaries)
# 각 decision_boundary에 대해 데이터셋을 생성하고 sigmoid 함수를 플롯
for decision_boundary, y in zip(decision_boundaries, Y):
plt.scatter(decision_boundary, y, color='b')
x_values = np.linspace(-10, 10, 400)
y_values = sigmoid(x_values, a, b)
plt.plot(x_values, y_values, color='r')
plt.show()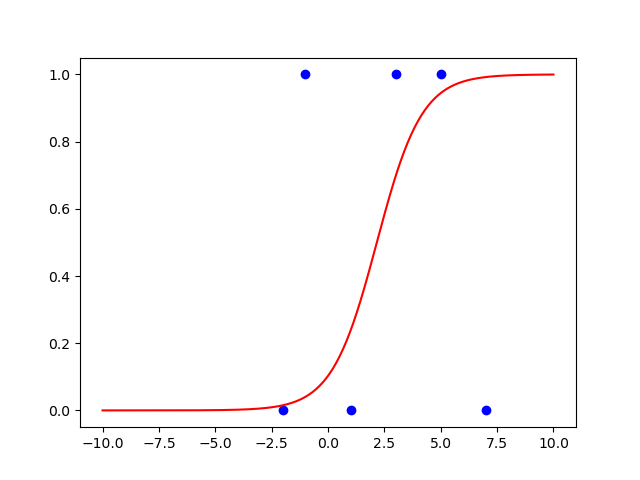
내일부터는 코드 결과를 바로바로 저장해야겠다... 오늘은 조금 귀찮
Sigmoid의 미분
- NOTE:
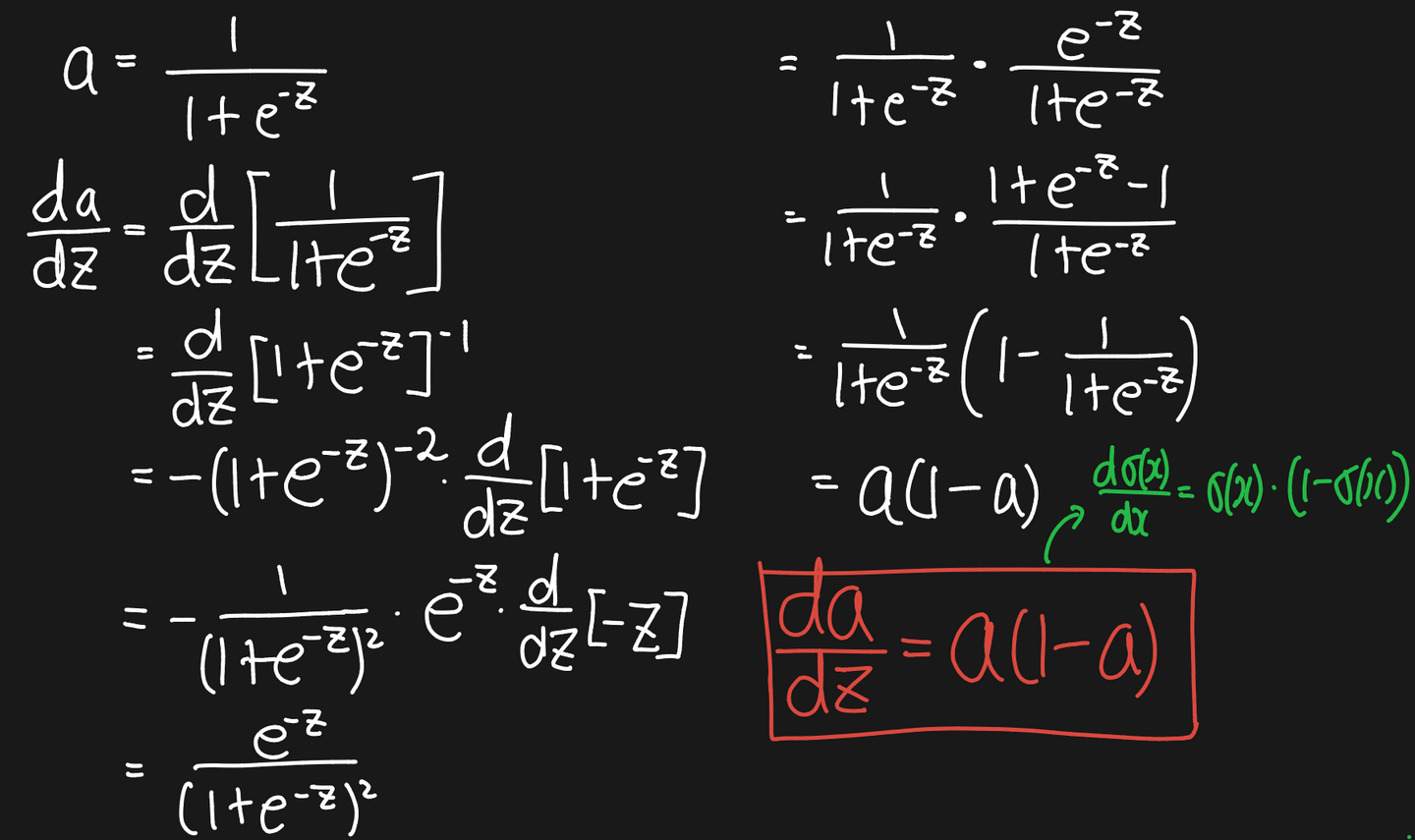
Sigmoid의 구현
import numpy as np
class Sigmoid:
def __call__(self, z):
self.a = 1 / (1 + np.exp(-z))
return self.a
def derivative(self):
return self.a * (1 - self.a)