Gradient Checking

Yelim Kim·2021년 8월 25일

Gradient Checking Gradient check N-Dimensional Gradient Checking

Machine_Learning

목록 보기

10/44

Gradient Checking에 대해서 알아보자. 이는 back propagation의 검증을 위해 꼭 필요한 단계이다.

Packages

import numpy as np
from testCases import *
from public_tests import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector

%load_ext autoreload
%autoreload 2

먼저 1D Gradient checking부터 확인해보자.

1-Demensional Gradient Checking

알고있는 1D 선형 함수를 생각해보자.

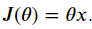
세타라는 parameter가 있고, x를 input으로 하는 선형함수이다. 여기서 반대로 J와 J의 미분값을 계산해야 할 때, gradient checking을 이용해 J가 맞는지 아닌지 확인할 수 있다.

위 그림은 1D 선형 함수 모델의 진행 순서를 보여준다.
순서대로 함수를 빌드해보자.

Forward propagation

J를 구하기 위한 Forward propagation함수를 만들어보자.

def forward_propagation(x, theta):
    J = x*theta
    return J

x, theta = 2, 4
J = forward_propagation(x, theta)
print ("J = " + str(J))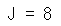

Backward propagation

dtheta값은 아래처럼 구할 수 있다.

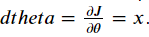
def backward_propagation(x, theta):
    dtheta = forward_propagation(x, theta)/theta
    return dtheta

x, theta = 2, 4
dtheta = backward_propagation(x, theta)
print ("dtheta = " + str(dtheta))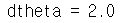

이제 이 부분에서 backward_propagation()함수가 정확히 dtheta값을 계산했는지 알아보기 위해 gradient checking을 도입한다.

gradapprox를 계산하기 위해서는

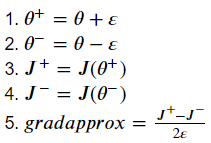
위 식을 대입하자.
그리고 backward_propagation을 이용해서 gradient를 계산하고 그 값을 grad에 넣는다.
마지막으로 gradapprox 와 grad의 difference를 아래의 식을 이용해 계산한다.

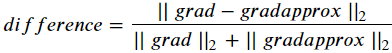
위 식을 계산하기 위해서 np.linalg.norm을 이용한다.
함수를 완성해보자.

def gradient_check(x, theta, epsilon=1e-7, print_msg=False):
    theta_plus = theta + epsilon
    theta_minus = theta - epsilon
    J_plus = forward_propagation(x, theta_plus)
    J_minus = forward_propagation(x, theta_minus)
    gradapprox = (J_plus - J_minus)/(2*epsilon)
    
    grad = backward_propagation(x, theta)
    
    numerator = np.linalg.norm(grad-gradapprox)
    denominator = np.linalg.norm(grad)+np.linalg.norm(gradapprox)
    difference = numerator/denominator
    
    if print_msg:
        if difference > 2e-7:
            print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
        else:
            print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference

x, theta = 2, 4
difference = gradient_check(2,4, print_msg=True)

difference가 10^-7보다 작으므로 backward_propagation에서 계산이 맞았다.
이제 N-D에서 Gradient checking을 확인해보자.

N-Dimensional Gradient Checking

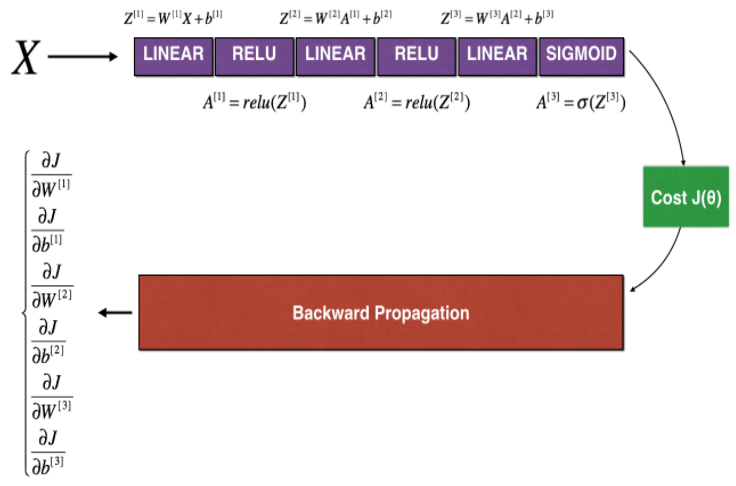
모델의 순서도다. 1D에 비해 parameter들이 많아지긴 했지만 전체적인 함수부분은 똑같다. 자세히 살펴보자.

Forward Propagation

def forward_propagation_n(X, Y, parameters):
    m = X.shape[1]
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)
    
    # Cost
    log_probs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
    cost = 1. / m * np.sum(log_probs)
    
    cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
    
    return cost, cache

Backward Propagation

def backward_propagation_n(X, Y, cache):
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1. / m * np.dot(dZ3, A2.T)
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
    
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1. / m * np.dot(dZ2, A1.T)
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
    
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1. / m * np.dot(dZ1, X.T)
    db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
                 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
                 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

여기서 만약에 숫자를 잘못 입력하게되면 아래에서 오류가 나게된다.
위에서 작성한 backward propagation()함수는 오류를 수정한 버전이다.

아래 gradient check로 맞나 확인해보자.

Gradient check

def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7, print_msg=False):
    parameters_values, _ = dictionary_to_vector(parameters)
    
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    
    for i in range(num_parameters):
        theta_plus = np.copy(parameters_values)
        theta_plus[i] = theta_plus[i] + epsilon
        J_plus[i],_ = forward_propagation_n(X, Y, vector_to_dictionary(theta_plus))
        
        theta_minus = np.copy(parameters_values)
        theta_minus[i] = theta_minus[i] - epsilon
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(theta_minus))
        
        gradapprox[i] = (J_plus[i]-J_minus[i])/(2*epsilon)
        
    numerator = np.linalg.norm(grad-gradapprox)
    denominator = np.linalg.norm(grad)+np.linalg.norm(gradapprox)
    difference = numerator/denominator
    
    # YOUR CODE ENDS HERE
    if print_msg:
        if difference > 2e-7:
            print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
        else:
            print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")

    return difference

X, Y, parameters = gradient_check_n_test_case()

cost, cache = forward_propagation_n(X, Y, parameters)
gradients = backward_propagation_n(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y, 1e-7, True)
expected_values = [0.2850931567761623, 1.1890913024229996e-07]
assert not(type(difference) == np.ndarray), "You are not using np.linalg.norm for numerator or denominator"
assert np.any(np.isclose(difference, expected_values)), "Wrong value. It is not one of the expected values"

만약 위에 backward propagation()에서 실수를 했다면 위 함수를 돌렸을 때

이런 비슷한 결과가 출력될 것이다.
그렇다면 다시backward propagation() 함수로 돌아가 오류를 수정하면 된다.