우선 $y=ax+b$라는 그래프를 생각해보자.
이 그래프는 좌표평면을 이등분한다.

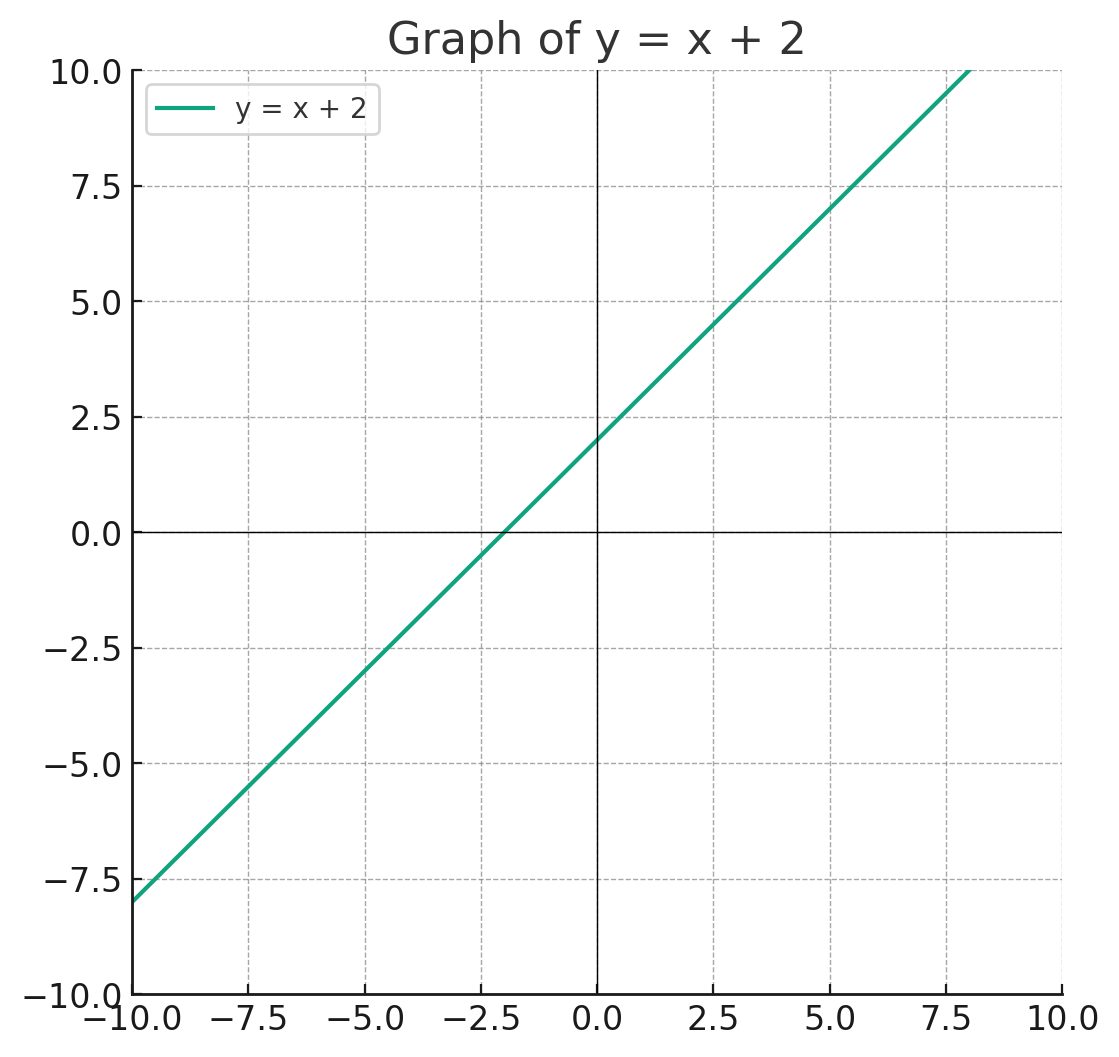
위 초록색 직선을 기준으로 만약 y가 x+2보다 크다면 위쪽 부분에, 작다면 직선 아래쪽 부분에 있을 것이다.
특징을 적어보자.

• $\mathbb{R}^2$안에 존재하면서 $\mathbb{R}^2$를 이등분한다.
• 1차원 스페이스

여기서 1차원 스페이스란, 직선을 의미한다. 만약 여러분이 개미이고 저 직선 위에만 존재한다면 아마 그건 1차원의 공간일 것이다. 앞 아니면 뒤로만 이동할 수 있다.

이번에는 차원을 높여보자.
$z=ax+by+c$의 그래프를 그려보자.

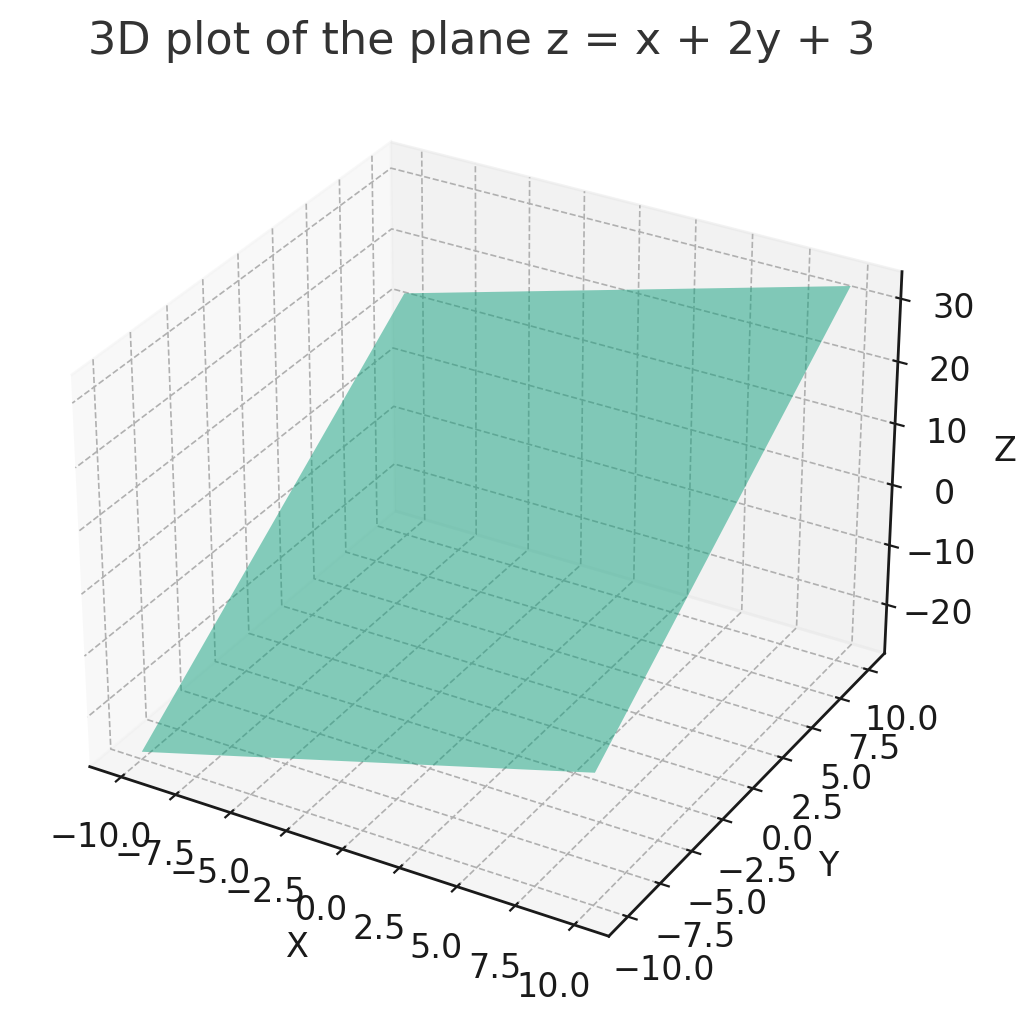
이 그래프의 특징은

• 공간 좌표$\mathbb{R}^3$안에 존재하면서 $\mathbb{R}^3$을 양분한다.
• 2차원 스페이스이다.

수식을 $z=ax+by+c$라고 써서 그렇지, 변수를 바꿔보면 우리에게 익숙한 방정식이 보일 것이다.

만약 조금 더 차원을 높인다면?

이면 "평면 비스무레 한 것" 이라고 할 수 있겠다.
특징은 아마도,

• 공간 좌표$\mathbb{R}^4$안에 존재하면서 $\mathbb{R}^4$을 양분한다.
• 3차원 스페이스이다.
  일 것이다.

이런 것들을 우리는 Hyperplane(초평면) 이라고 부른다.

Hyperplane이란, n차원 공간상에서 linear성질을 갖으며, 그 차원을 양분하는 평면이다.

Artificial Neuron의 Decision Boundary(결정경계)

지난 글에서 Decision Boundary를 설명한 적이 있다.

출력을 분류하는 기준 선 (함수)

라고 했었는데 Sigmoid로 예를 들어보면, Sigmoid의 분류기준은

이런 기준을 가지고 있었다.

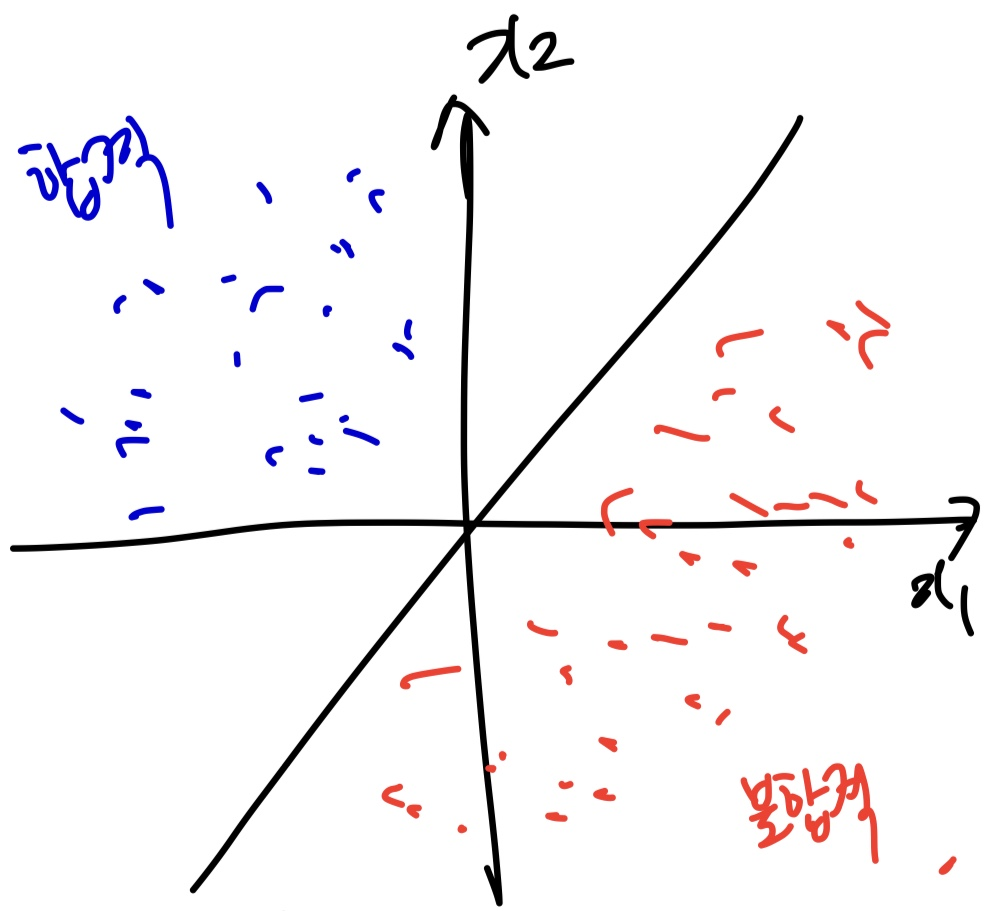
이번에는 이런 분포를 가지고 있는 예시를 들어보자.

어떤 시험에 합격 한 사람은 파란색 점들이고, 불합격한 사람들은 빨간색 점들이다.
이 두 사람들의 결과를 하나의 직선으로 분리할 수 있다.

방금은 우리가 했지만 이 일을 뉴런이 학습하고 나눌 수 있다!

Artificial Neuron은 직선, 평면과 같은 decision boundary밖에 만들지 못한다.
그런데 만약 이런 분포가 있다면 어떻게 될 것인가?

이 파란 점과 빨간 점을 어떤 직선이나 평면으로 정확히 구분지을 수 있을까?

할 수 없다.

그렇다면 어떻게 해야할까?

해결법

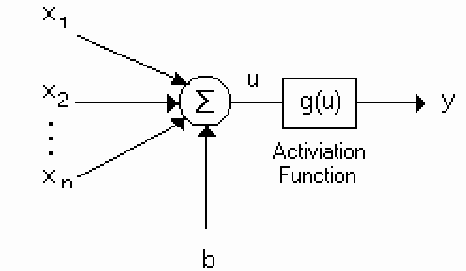
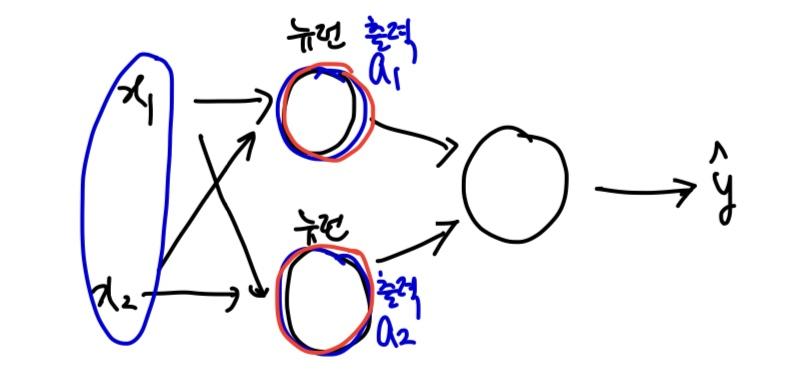
우리는 지금까지 한개의 뉴런을 사용했다.

출처 : Application and Comparison of Several Artificial Neural Networks for Forecasting the Hellenic Daily Electricity Demand Load - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/A-single-artificial-neuron-network_fig2_247157203 [accessed 13 Jul, 2023]

그래서 뉴런은 이렇게 구성되었다.

하지만 뉴런을 두개 사용한다면 어떤 일이 벌어질까?

$x_1, x_2$를 두 개의 뉴런이 같이 입력받는다.
그리고 각각 파라미터를 업데이트하고 출력한다.
그리고 다음 뉴런에게 출력값을 넘겨준다.

아까 뉴런은 '필터'라고도 얘기했었는데, 필터 2개, 다른 weight가 의미하는 게 무엇일까?

Decision Boundary가 다르다

는 것을 의미한다.
아까 살펴봤던 데이터를 다시 예시로 가져와보자.

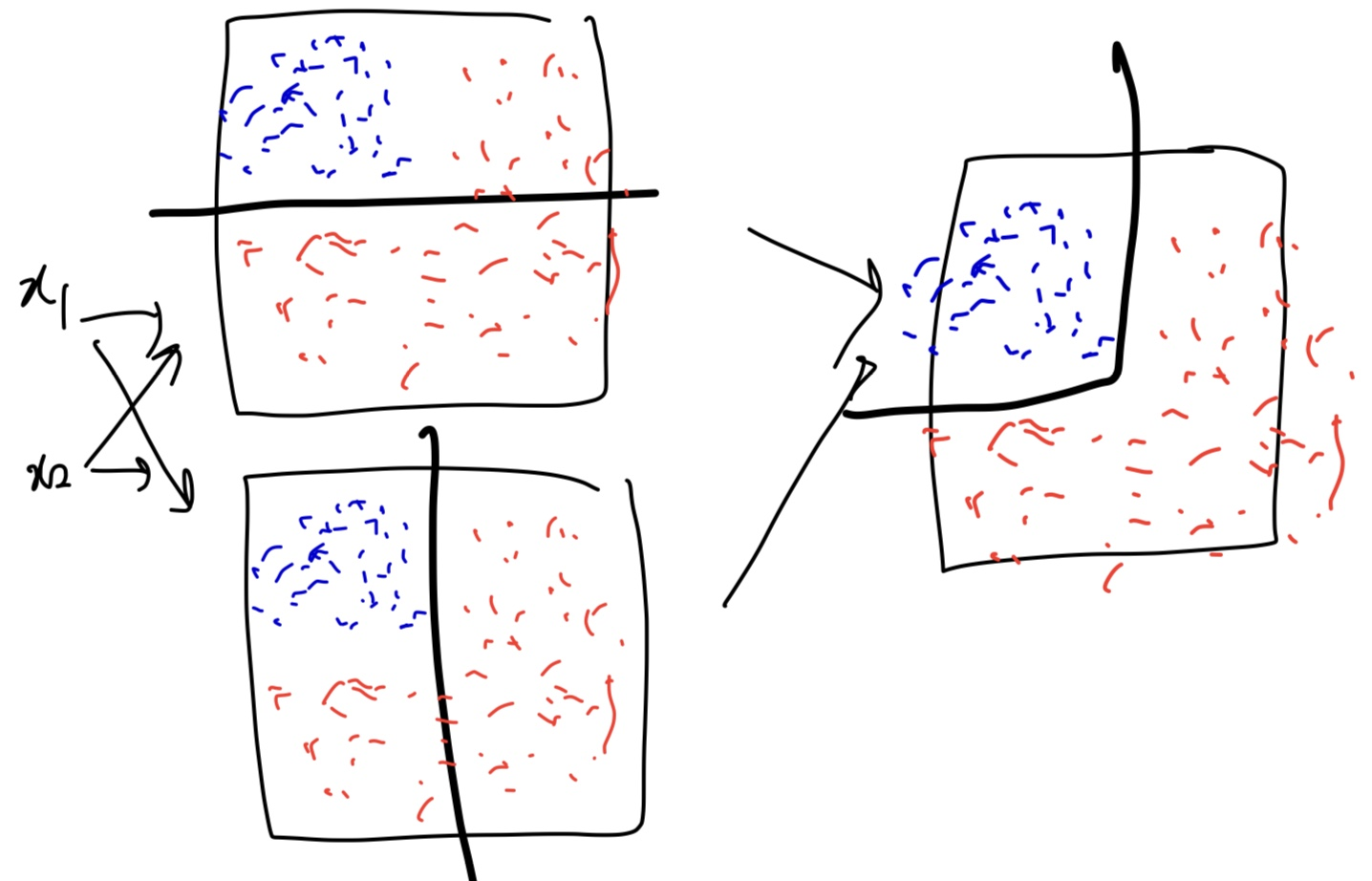
우리가 해결하지 못했던 이 데이터를 두개의 뉴런에게 학습시켜보면,

이런 현상이 발생한다.
즉, 더욱 더 복잡한 decision boundary를 만들 수 있게 된 것이다.
즉, 더욱 더 복잡한 dataset을 구분할 수 있게 됐다.

이 동영상은 뉴런 3개를 이용해서 학습을 한다. 정확히 어떻게 학습이 되는지 볼 수 있다.
동영상에서 나타내는 것을 같은 방식으로 그려보았다.

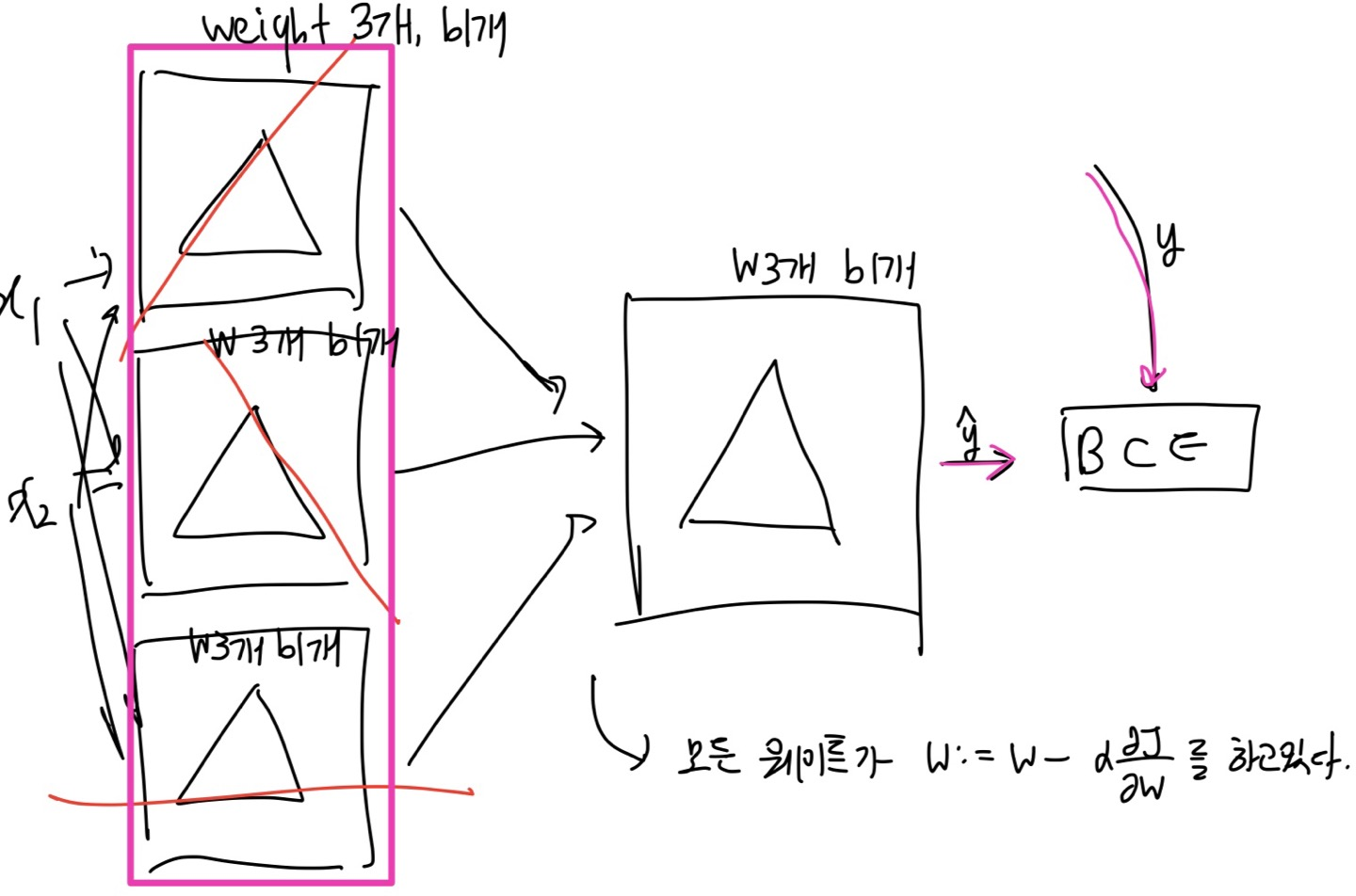
여기서 왼쪽 핑크색 네모친 부분을 하나의 레이어라고 한다.
레이어는 같은 입력을 받는 뉴런들의 집합이다.

• 레이어의 각각의 뉴런은 다른 w , b값을 가진다.
• 레이어의 각각의 뉴런의 입력값은 같다. 즉, w와 b의 개수가 같음을 의미한다.

첫 번째 레이어에서 각각의 뉴런은 3개의 weight와 1개의 bias를 갖는다.
두 번째 레이어에서 뉴런은 3개의 weight와 1개의 bias를 갖는다.

모든 웨이트가 $w:=w-\alpha \frac{\partial J}{\partial w}$를 하고 있다고 생각하면 된다.

하지만 앞으로는 우리가 뉴런의 개수를 정하기 보다는, 이미 성능이 검증된 모델을 사용하기 때문에 몇개를 설정해야 할지에 대한 걱정은 하지 않아도 좋다. 하지만 꼭 필요한 개념이다.

이 개념을 기반으로 다음 내용을 알아보자

Multilayer Perception

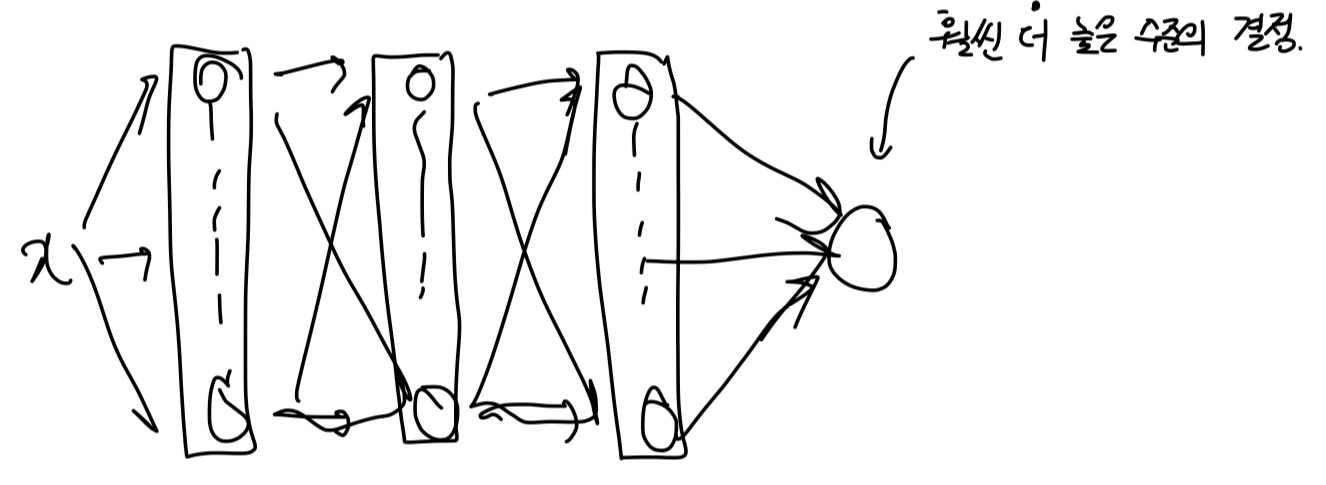
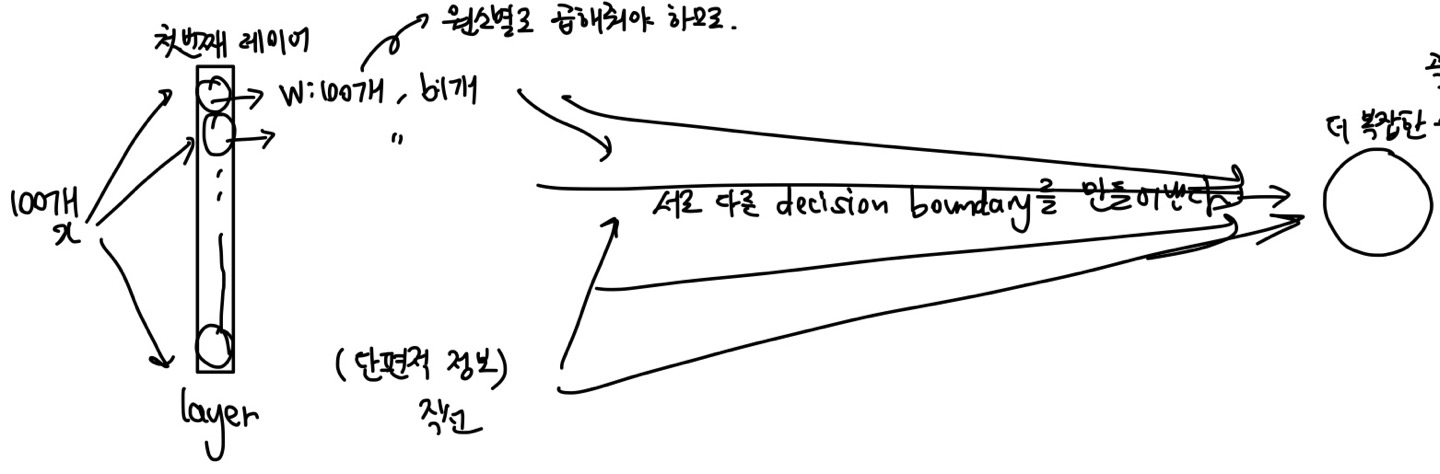
이번에는 입력으로 100개의 x값을 넣는다.
그리고 대박많은 뉴런을 배지한다.
첫번째 레이어의 각각의 뉴런은 100개의 weight와 1개의 bias를 갖는다.
그리고 서로 다른 decision boundary를 만들어 내어 매우 복잡한 수준의 의사결정을 할 수 있을 것이다.

하지만 이 개념의 제목을 보면 Multilayer이다. 레이어가 많아야 한다는 뜻이다.
위 내용을 이해했다면 아래 그림도 이해할 수 있을 것이다.

우리가 앞으로 마주할 많은 모델들은 많은 레이어와 많은 뉴런들을 가진다.
따라서 더욱 더 높은 수준의 결정을 할 수 있게 되고 더 복잡한 함수를 만들 수 있게 된다.

예시를 들어보자면,
하나의 레이어를 직급이라고 생각하면 쉽다.
어떤 x라는 문제가 들어왔을 때, 첫번째 레이어는 '사원'이다. 각각의 사원들이 이 문제에 대해서 생각하고 각자의 방법으로 결론을 낸다. 그 결론은 각자의 상사에게 전달된다.
두번째 레이어는 '팀장'이라고 하자. 이 팀장들도 사원에게 들은 결론을 이용하여 팀장의 결론을 내린다.
세번째 레이어는 '부장'이라고 하자. 이 부장들도 팀장에게 들은 결론을 이용하여 부장의 결론을 내린다.
마지막은 '사장'이다. 사장은 이 모든 의견을 반영하여 매우 고차원적인 결정을 하게 된다.

이것이 Multilayer Perception이다.

다음에는 실제 데이터를 이용해서 코드를 짜보자.