
Neural Network를 하면서 맨 처음에 하는 일, weights와 bias를 초기화하는 일에 대해 조금 더 깊이 알아보려고 한다. 여기서 weight와 bias를 잘 초기화한다면, 조금 더 빨리 원하는 결과에 도달할 수 있을 것이다.
만약 parameter들이 좋은 초기화값을 가졌다면, 그 모델은 gradient descent를 더 빨리 수렴할 수 있을것이고, 적은 error을 낼 수 있을 것이다. 바로 시작해보자.
Packages
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from public_tests import *
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
# load image dataset: blue/red dots in circles
# train_X, train_Y, test_X, test_Y = load_dataset()train_X, train_Y, test_X, test_Y = load_dataset()코드를 더해 데이터를 visualize해보자.
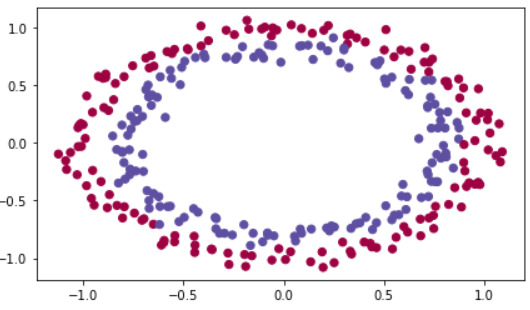
제목에서 이미 언급했다시피, 이 데이터는 blue/red dots in circles이고, 아마 여기서 파란색과 빨간색을 분리하고 싶을 것이다.
이 글에서는 Initialize에만 집중할 것이기 때문에 아래 모델 코드는 크게 신경쓰지 않아도 된다.
def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
grads = {}
costs = [] # to keep track of the loss
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 10, 5, 1]
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
# Loop (gradient descent)
for i in range(num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
a3, cache = forward_propagation(X, parameters)
# Loss
cost = compute_loss(a3, Y)
# Backward propagation.
grads = backward_propagation(X, Y, cache)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 1000 iterations
if print_cost and i % 1000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
costs.append(cost)
# plot the loss
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters모델을 만들어주었다. 이제 Initialize에 대해서 알아보자.
먼저 weights와 bias를 0으로 초기화해보자.
Zero Initialization
def initialize_parameters_zeros(layers_dims):
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parametersparameters = initialize_parameters_zeros([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))그 결과다.
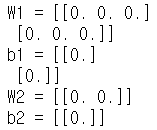
이 parameter를 가지고 모델을 학습시키면서 cost를 동시에 출력시켜보자.
parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)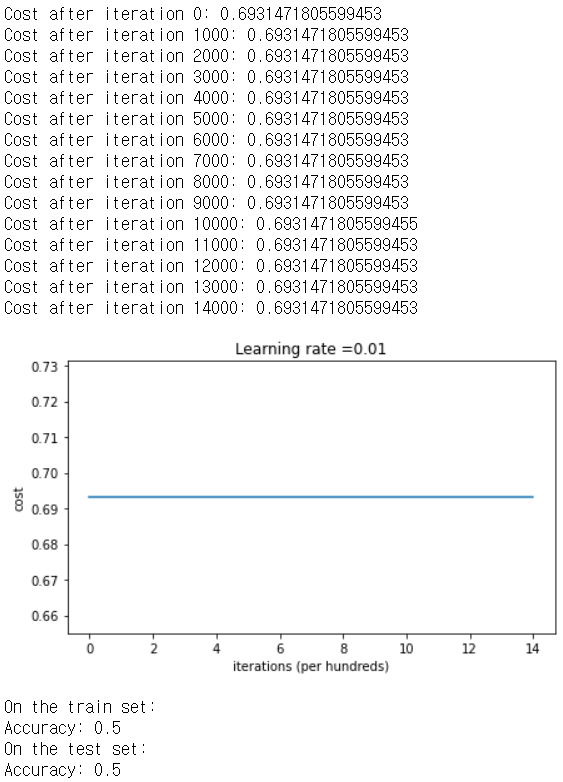
cost가 전혀 줄지 않았다. 아무것도 학습하지 못했다는 뜻이다. 왜 이런일이 발생할까?
predictions와 decision boundary를 살펴보자.
print ("predictions_train = " + str(predictions_train))
print ("predictions_test = " + str(predictions_test))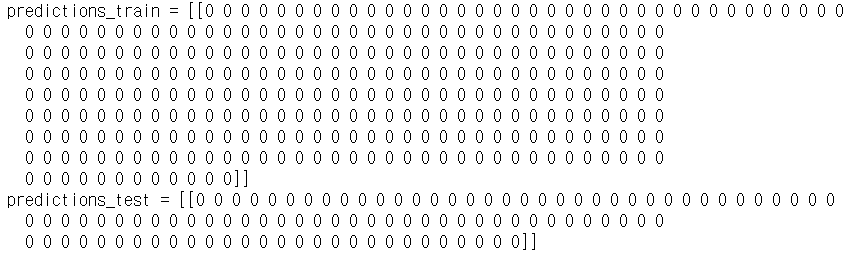
plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)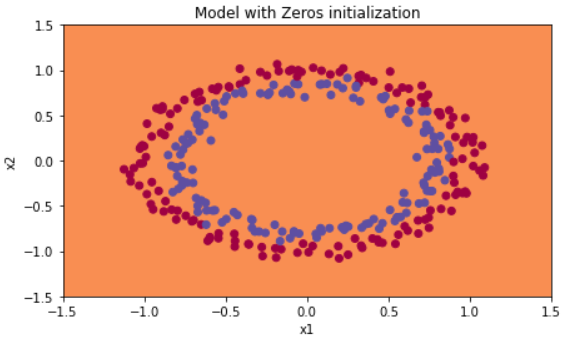
각각의 input들을 weight와 곱할때, 만약 weights가 0이면 그 전체값도 0이 되고 만약 활성화 함수가 ReLU라면 아래와 같이 값이 0인 벡터를 생성한다.
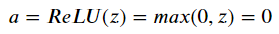
만약 sigmoid라면
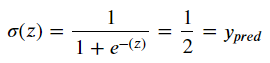
z=0일 때, 1/2의 값을 얻게 되는데, 이는 모든 샘플에서 같은 값의 Loss func값이 나오게 된다. 아래 식 Loss function을 봐 보자.
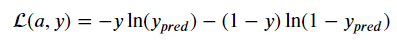
만약 y=1 이고 y_pred=0.5라면 위의 값은
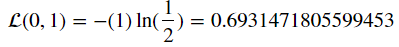
이런 값이, y=0 이고 y_pred=0.5라면
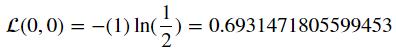
함수를 통과한 값은 항상 일정한 0.5이므로 같은 Loss function의 값이 나오게 된다.
따라서 weight는 반드시 랜덤값으로 초기화 되어야한다.
bias는 직접 곱해주는 parameter가 아니기 때문에 0이어도 상관없다.
랜덤으로 초기화해보자.
Random Initialization
아래 코드에서는 np.random.randn을 사용하여 weight값을 랜덤초기화하며, 각각의 값에 *10을 하여 크게 만들어줄 것이다.
def initialize_parameters_random(layers_dims):
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims)
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*10
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parametersparameters = initialize_parameters_random([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
마찬가지로 모델에서 학습시켜보자.
parameters = model(train_X, train_Y, initialization = "random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)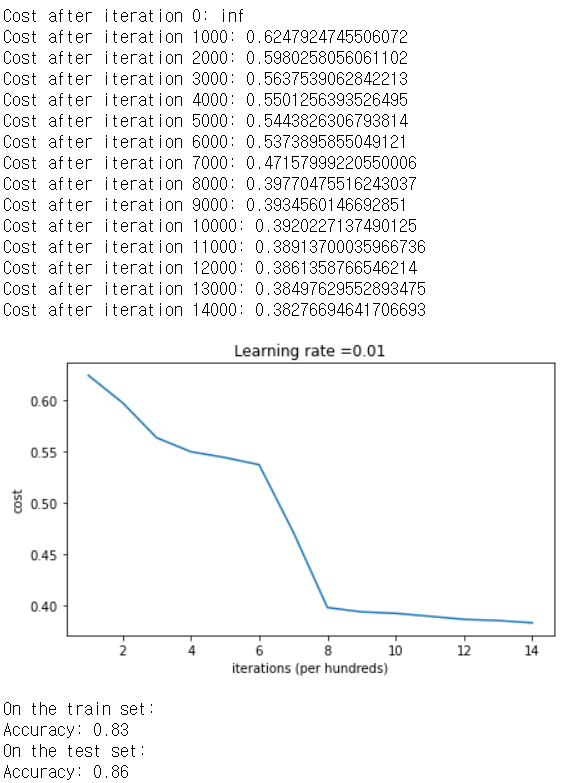
아까보다 좋은 결과가 나왔다.
Cost after iteration 0 : inf는 숫자 반올림 때문인데, 수치를 조금 더 정교하게 구현하면 문제가 해결되겠지만 여기서는 신경쓰지 않아도 괜찮다.
여기서도 predictions_train과 test를 출력해서 확인해보자.
print (predictions_train)
print (predictions_test)
plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)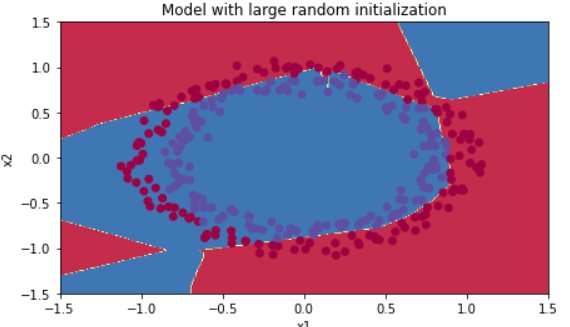
학습이 썩 잘되진 않은 모양이다. 우선 cost의 시작값이 굉장히 크고 마지막 손실도 크다. 처음부터 초기화값을 크게 줬기 때문인데, 아래서 다시 해결해보도록 하자. 방금은 랜덤초기화한 값에 10을 곱해줬었는데, 이보다 작게, 그렇다면 얼마나 작게 해줘야할까?
아래서 살펴보자.
He Initialization
He는 이 이론을 처음 만들어 낸 사람의 이름이다. He initialization은 ReLU함수에서 weight에 10대신, 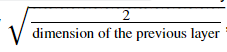
위 식과 같은 수를 곱하라고 제안한다.
10 대신 위 식을 대입해보자.
def initialize_parameters_he(layers_dims):
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims) - 1 # integer representing the number of layers
for l in range(1, L+1):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*np.sqrt(2./layers_dims[l-1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parametersparameters = initialize_parameters_he([2, 4, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
모델에서 학습시켜보자.
parameters = model(train_X, train_Y, initialization = "he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)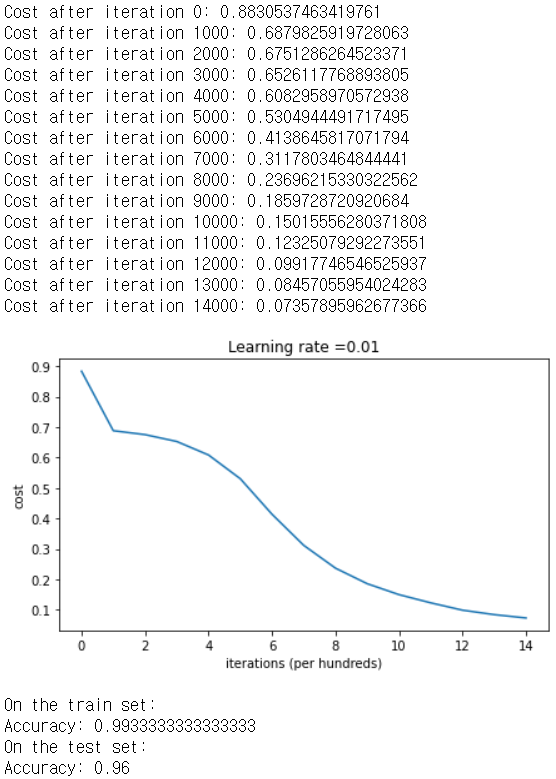
plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
빨간색과 파란색의 점들을 잘 구분해냈다.
Conclusions
위에서 세가지의 Initialization들을 시도해봤다. 각각을 비교해보자.

이제 어떻게, 어떤값으로 초기화 해야하는지 조금 더 명확해졌다.
