순환 신경망 Recurrent Neural Network(RNN)

RNN은 기본적으로 '시간 개념이 있는 데이터'들을 처리하기 위한 신경망이다.

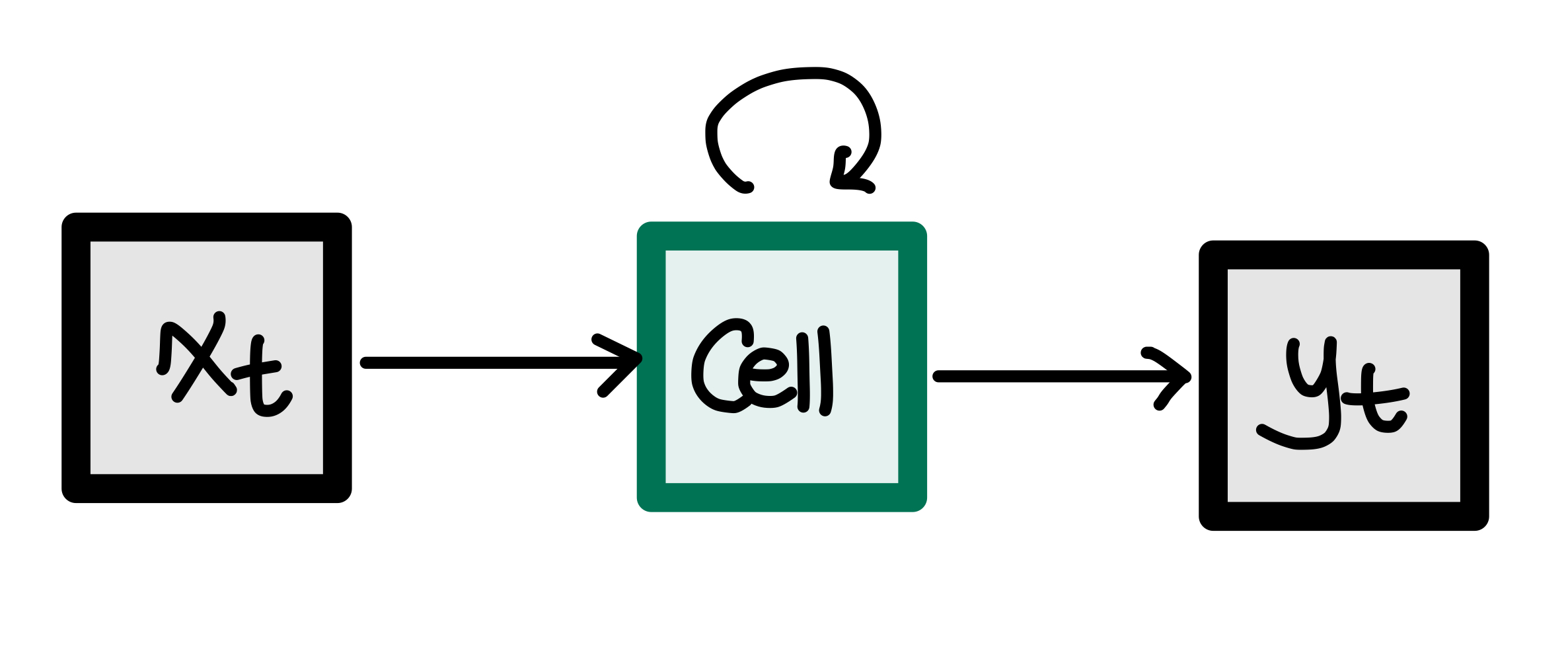
xt는 현재의 입력으로써, 입력을 받은 후 Cell에서 루프를 사용하여 입력에 대한 출력값을 다시 입력으로 사용하게 된다. 따라서 yt는 과거와 현재의 정보를 동시에 반영한 출력값이다.

Numpy로 이 순환 신경망을 구현해보자.

Numpy 로 순환 신경망 구현하기

import numpy as np

timesteps = 10        # 문장의 길이
input_dim = 4         # 단어 벡터의 차원
hidden_size = 8       # 은닉 상태의 크기(메모리 셀의 용량)

inputs = np.random.random((timesteps, input_dim))   #입력

hidden_state_t = np.zeros((hidden_size,))     #hidden_size로 은닉 상태 만들기

print(hidden_state_h)

위 코드에서처럼 8의 크기를 갖는 은닉 상태를 출력해보자.
우리가 hidden_state_t = np.zeros((hidden_size,))에서 초기화 했듯이 모든 차원이 0의 값을 가지게 될 것이다.

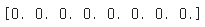
이제 0이 아닌 다른 차원의 2D 텐서를 생성해보자. 가중치를 초기화 해 준다.

Wx = np.random.random((hidden_size, input_dim))   # (8,4)크기의 입력에 대한 가중치
Wh = np.random.random((hidden_size, hidden_size)) # (8,8)크기의 은닉 상태에 대한 가중치
b = np.random.random((hidden_size,))              # (8,)크기의 bias생성

( np.random함수에 대한 설명은 여기를 참고하자 )

초기화를 할 때 음수값으로 초기화 하지 않는 이유?
random.randn을 쓰지 않고 random.random을 쓰는 이유?

parameters을 초기화 해 줬으니, 이제 순환 신경망을 구현해보자.
RNN은 시점에 따라서 입력을 받는데, 현재 시점의 hidden_state인 ht연산을 위해 그 직전 시점의 hidden_state인 h(t-1)을 입력받는다.

위 은닉층의 식에서 Wh*h(t-1)을 없애면 우리가 알고있는 신경망과 수식이 같아지는 것을 볼 수 있다. 이 식을 추가해주었기 때문에 RNN은 과거의 정보를 기억할 수 있는 것이다.

본격적으로 구현해보자.

total_hidden_states = []

#메모리 셀(hidden_size)동작
for input_t in inputs:    #각각의 글자가 입력됨
    output_t = np.tanh(np.dot(Wx, input_t) + np.dot(Wh, hidden_state_t) + b)
    total_hidden_states.append(list(output_t))  # 각 시점의 은닉 상태의 값을 계속해서 추적
    print(np.shape(total_hidden_states))
    hidden_state_t = output_t     #출력값을 다시 입력값으로
    
total_hidden_states = np.stack(total_hidden_states, axis = 0)   #출력시 한줄로 나열되지 않게 해준다

print(total_hidden_states)

이런 출력값이 나온다.

순환 신경망 구현 이해하기

이제 이 SimpleRNN ( 위에서 설명했던 RNN )이 어떻게 사용되는지, 각각의 변수들은 어떤 의미를 가지고 있는지 알아보자.

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import SimpleRNN, Bidirectional, LSTM, GRU

model = Sequential()
model.add(SimpleRNN(3, input_shape=(2,10)))
model.summary()

위 코드에서 model.add(SimpleRNN(3, input_shape=(2,10)))은
model.add(SimpleRNN(3, input_length=2, input_dim=10))와 동일하다.
input_length = time_step(시점)이다.

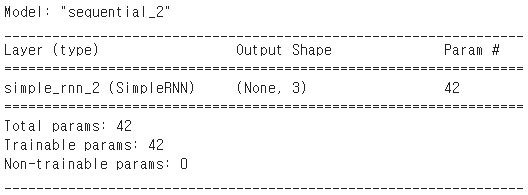
위와같은 출력결과를 얻게 된다.
여기서 우리는 왜 parameter값이 42가 되는지 생각해 볼 필요가 있다.
아래 그림을 참고하면 도움이 된다.

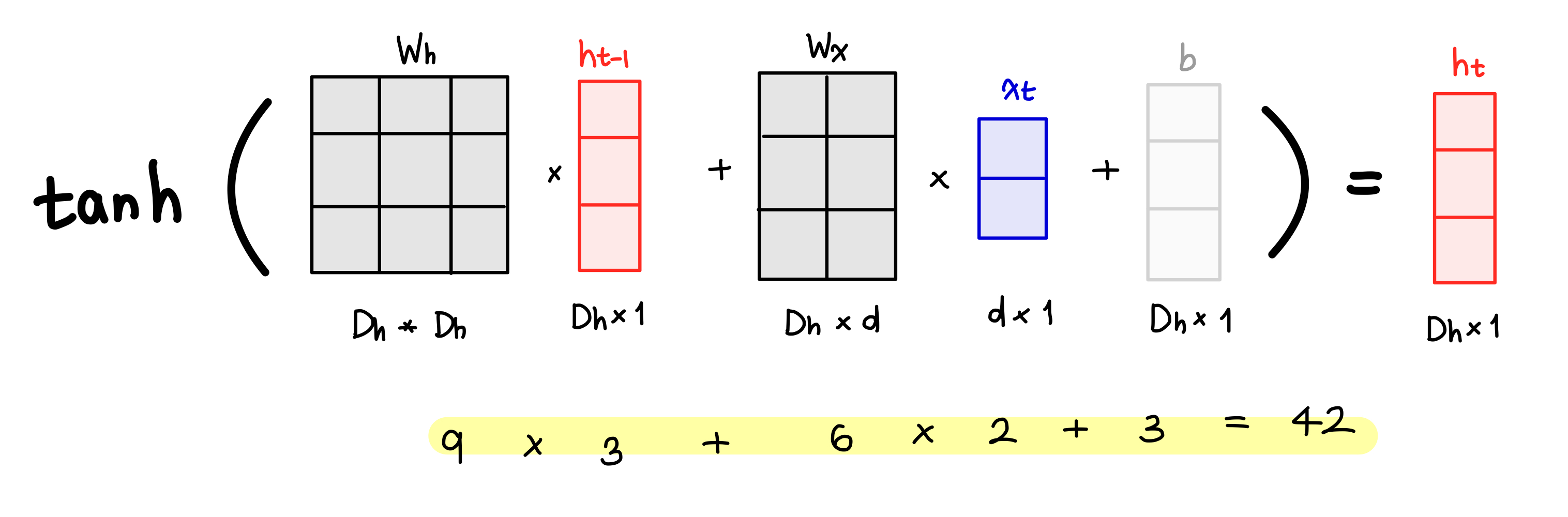
여기서 Dh = hidden_size, 즉 SimpleRNN(3, 에서의 3이다.
d는 임베딩값이다.

Summary에서 Output Shape이 (None, 3)인 이유는 우리가 아직 batch_size의 값을 알지 못해서이다. 이번에는 batch_size를 미리 정의해보자.

model = Sequential()
model.add(SimpleRNN(3, input_shape=(10,10), return_sequences=True))
model.summary()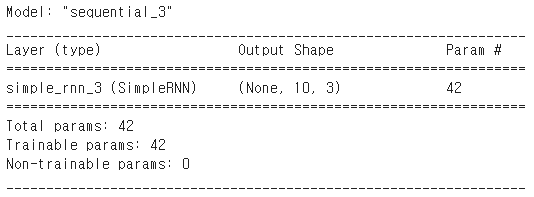

input_shape의 차원을 바꾸고, return_sequences=True로 설정하면 3D 텐서를 리턴할 수 있다.
위의 출력값과 비교해보면 달라진 값은 Output Shape이다. 여기서 timesteps(문장의 길이) = 10이 추가되었다.

batch_size를 기재해보자.

model = Sequential()
model.add(SimpleRNN(3, batch_input_shape=(8,2,10), return_sequences=True))
model.summary()

출력의 크기가 (8,2,3)이 되었다.

이제 이 기본 RNN모델을 가지고 다양한 모델을 만들어보자.

은닉층이 2개인 Deep RNN

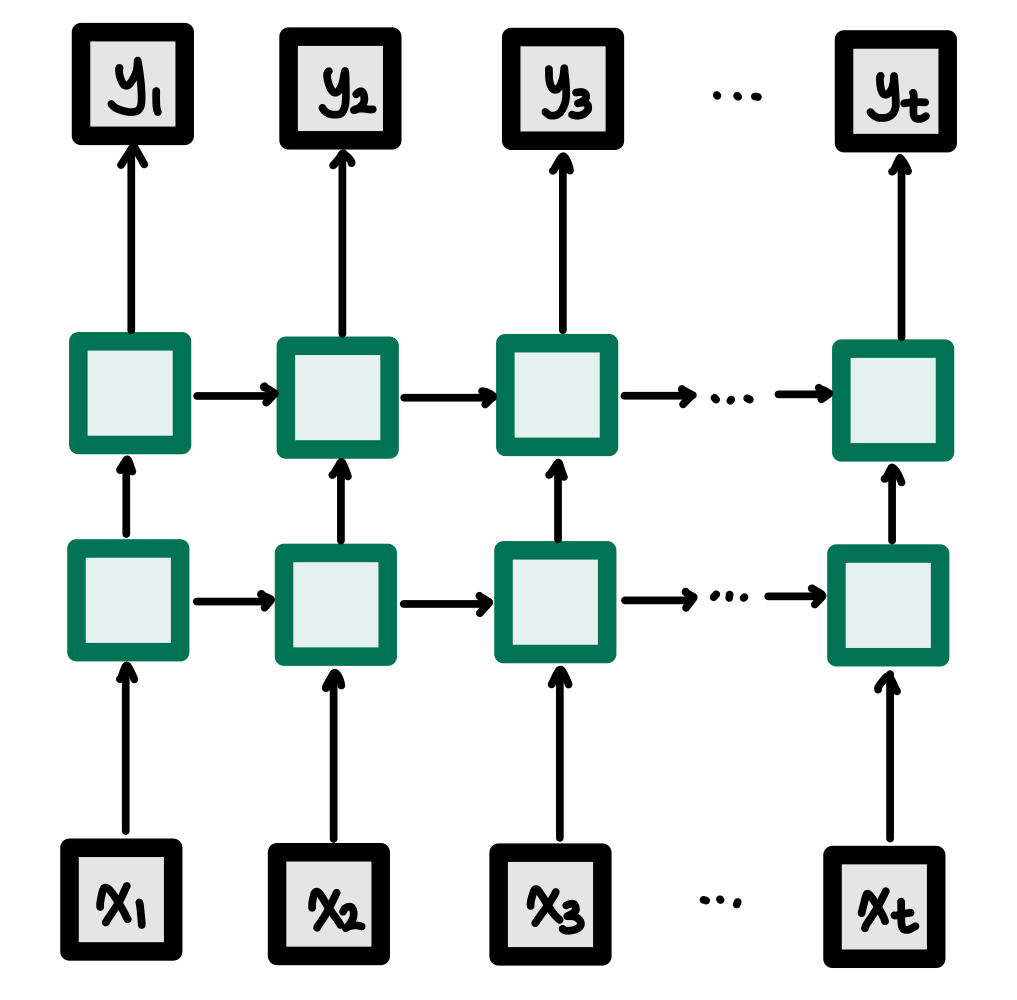
RNN의 입력층을 높인 모습이다.
여기서 주의해야할 부분은 각 층의 Wh, Wx 가중치의 값은 같다는 것이다.
코드로 구현하면 아래와 같다.

model = Sequential()
model.add(SimpleRNN(hidden_size, return_sequences = True))
model.add(SimpleRNN(hidden_size, return_sequences = True))

return_sequences = True로 설정하게 되면 출력이 yt만 나오는게 아니라 y1부터 yt전체가 나오게 된다.

양방향 순환 신경망 (Bidirectional RNN)

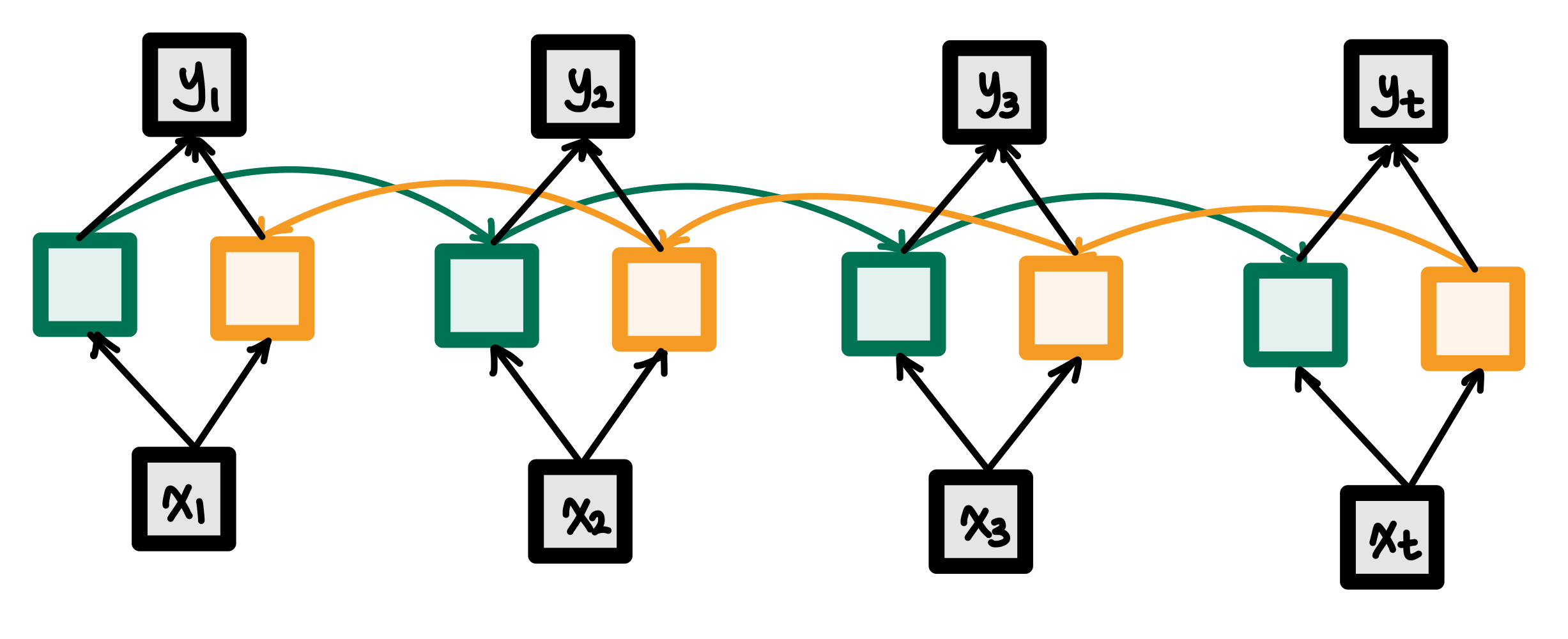
위 그림처럼 역방향으로 입력을 참고하는 RNN을 추가할 수 있다. 이 모델은 결정할 때마다 양쪽의 문맥을 동시에 보는 특징이 있다.
이런 모델을 사용하는 이유는 아래와 같은 문제점이 생겼을 때 해결하기 위해서이다.

Exercise is very effective at ( ) belly fat.
1) Reducing
2) Increasing
3) Multiplying

위와 같은 문제를 해결하기 위해서는 앞의 문장만 고려할 것이 아니라, 문장의 뒷 부분도 알아야 하므로 Deep RNN같은 모델이 나오게 되었다.

model = Sequential()
model.add(Bidirectional(hidden_size, return_sequences = True), input_shape=(timesteps, input_dim)))

위와 같이 input_shape=(timesteps, input_dim)인자를 추가해서 만들어준다.

깊은 양방향 순환 신경망 (Deep Bidirectional RNN)

제목 그대로 Deep RNN과 Bidirectional RNN을 섞은 모델이다.
Bidirectional RNN모델에 층을 하나 더 추가한 모습이다.

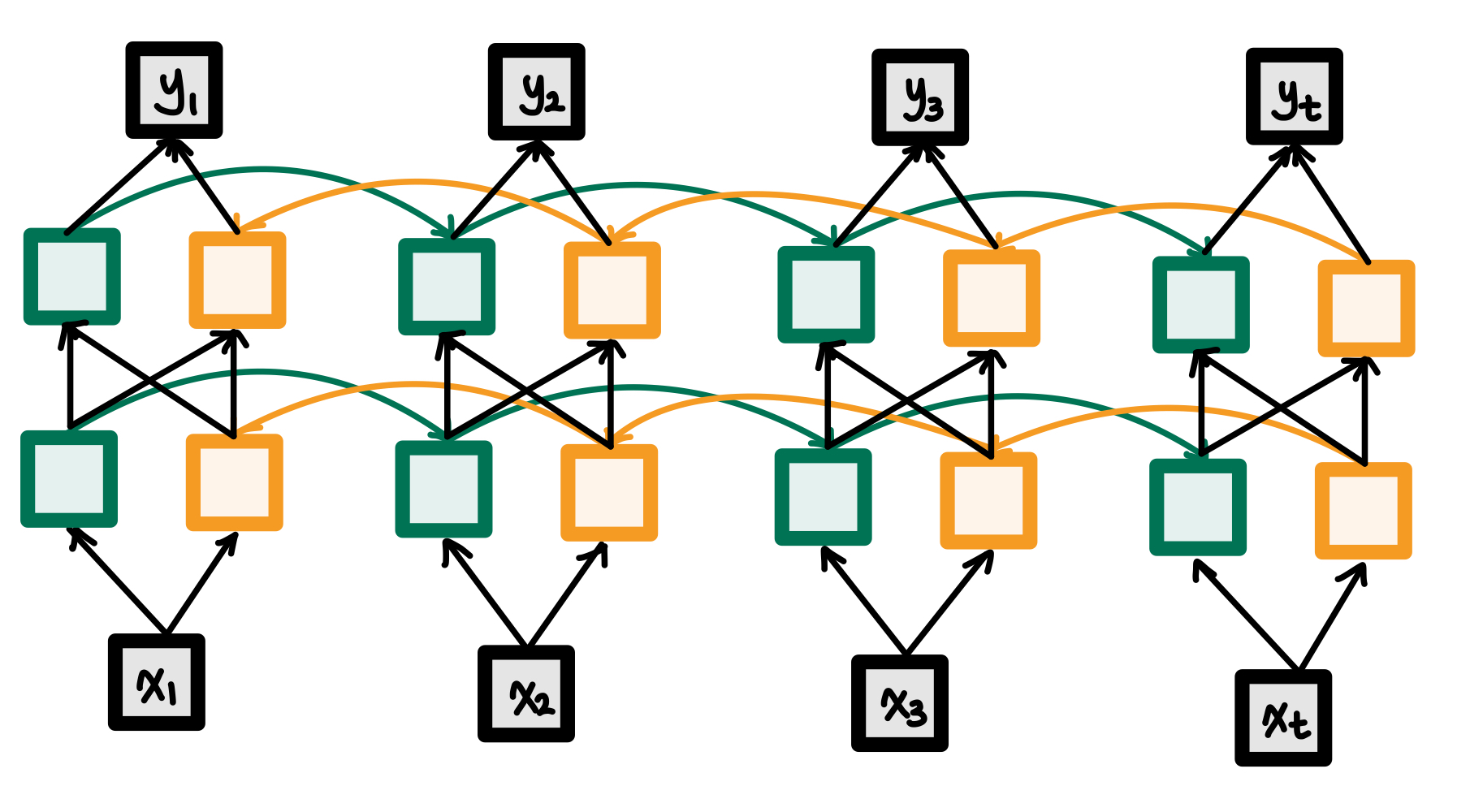
이 모델은 거의 2층으로만 사용하는데, 3층 이상으로 레이어를 쌓을 수록 효과가 거의 미미하기 때문이다.

model = Sequential()
model.add(Bidirectional(SimpleRNN(hidden_size, return_sequences = True), input_shape=(timesteps, input_dim)))
model.add(Bidirectional(SimpleRNN(hidden_size, return_sequences = True)))
model.add(Bidirectional(SimpleRNN(hidden_size, return_sequences = True)))
model.add(Bidirectional(SimpleRNN(hidden_size, return_sequences = True)))

위와 같이 구현할 수 있다.

LSTM구현하기 (Long Short-Term Memory)

기존 SimpleRNN모델은 장기 의존성 문제가 발생한다.이를 개선한 모델이 LSTM모델이다.

아래의 SimpleRNN 과 비교했을 때 어떤 부분이 달라졌는지 보자.

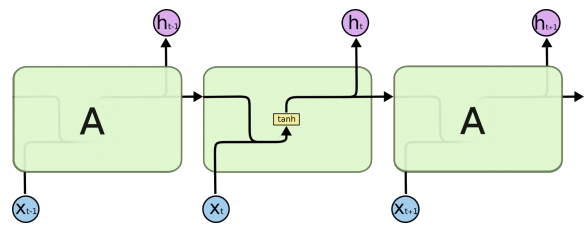
SimpleRNN

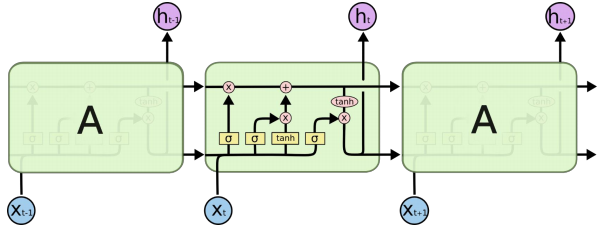
LSTM

많이 복잡해보이지만 우리가 여기서 주목해야 할 점은 Cell state가 추가되었다는 점이다. 위에서 설명했던 hidden state와 같이 이전의 cell state는 다음 시점의 입력이 된다.

위 그림에서 주의해야 할 부분이 있다.
위에서 설명했던 그림은 최고층이 출력이었지만 여기는 한 층의 모습만 나타내고 있다. 그 층의 출력값은 y가 아니고 h라는 것에 주의하자. LSTM은 다음 층에게 hidden state를 보내고 있다.

그리고 자세히 살펴보면, 옆의 RNN에게 두개의 출력값을 보내는데, 각각 cell state와 hidden state을 보내고 있다. cell state는 그저 장기 의존성 문제를 해결하기 위해, 즉 기억력을 높여주기 위해 추가한 것이므로 다음 층에는 보내지 않는다.

이 Cell state에 gate라는 구조를 통해서 정보를 더하거나 빼는 통제를 하는데,
현재 정보를 기억하기 위한 게이트인 입력 게이트(input gate)와 기억을 삭제하기 위한 게이트인 삭제 게이트(forget gate)가 있다.

입력게이트부터 살펴보자.

입력게이트 (Input gate)

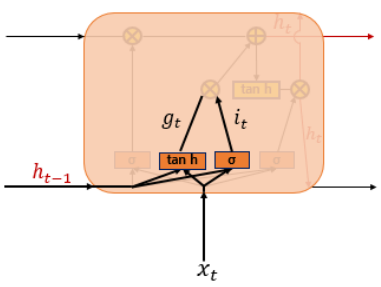
들어온 입력은 tanh함수와 sigmoid함수를 지나게 되고 Cell gate에서 이번에 기억할 값(it, gt중 한 값)을 선택하게 된다.

삭제 게이트 (Forget gate)

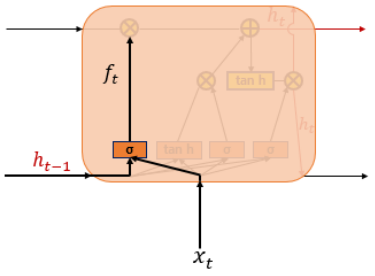
들어온 입력에 대해 sigmoid함수를 지나 0과 1사이의 값(ft)이 나오는데, 0에 가까울수록 정보가 많이 삭제된 것이며, 1에 가까울수록 정보를 온전히 기억했다는 뜻이다.

셀 상태 (Cell state)

이제 다시 cell state로 돌아와보자.

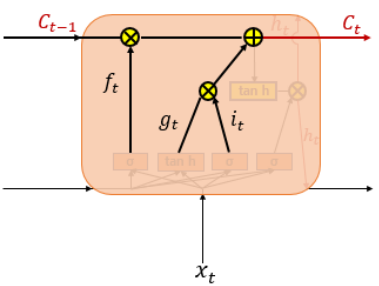
삭제 게이트에서 기억을 소실하고, 입력 게이트에서 이번에 기억할 값을 선택한다음, 아래 수식과 같이 두 값을 더하게 된다.

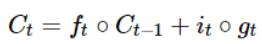
즉, 삭제 게이트는 이전 시점의 입력을 얼마나 반영할 지 결정하고, 입력 게이트는 현재 시점의 입력을 얼마나 반영하는지 결정한다.
이 둘은 가중치값을 가지고 있으므로, 학습을 통해 가중치 값을 업데이트하면서 얼마나 삭제하고 기억할지 결정하게 된다.

이제 마지막 부분인 출력게이트를 살펴보자.

출력 게이트 (Output gate)

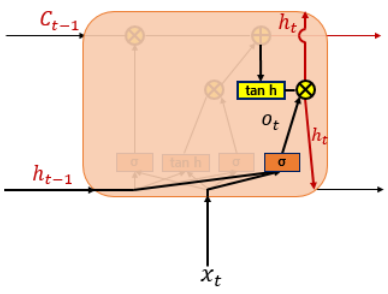
출력 게이트는 hidden state를 연산하는데 쓰인다.
위에 cell state를 바탕으로 필터링 된 값이 output gate로 출력될 것이다.
그림으로 확인해보면 먼저 sigmoid함수에 입력값을 넣고, cell state를 tanh함수에 넣어서 둘이 곱해준다. 이렇게 되면 우리는 output으로 보내고자 하는 부분만 내보낼 수 있다.

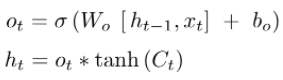
설명이 조금 길었다.
LSTM은닉층을 추가하는 코드는 그렇게 복잡하지 않다.

model = Sequential()
model.add(LSTM(hidden_size, input_shape=(timesteps, input_dim)))

Gated Recurrent Unit (GRU)

방금 위의 LSTM은 식이 많이 복잡하고 게이트가 3개(input, forget, output)나 있었다.
GRU는 없앨 수 있는 수식을 다 없애고, 게이트를 두개(update gate, reset gate)로 줄였다.
연산의 길이가 줄었기 때문에 가중치의 개수도 줄었다.

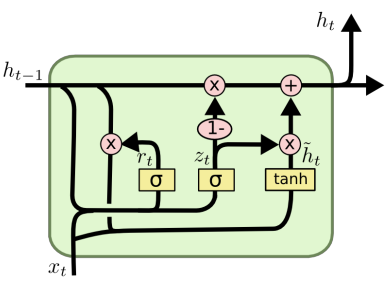
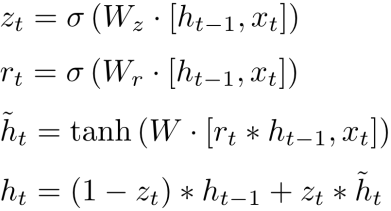
그렇다면 언제 LSTM을 쓰고 언제 GRU를 써야 할까?
데이터가 많다면, LSTM > GRU
데이터가 어중간하다면, LSTM < GRU

코드로 GRU은닉층을 추가해보자.

model = Sequential()
model.add(GRU(hidden_size, input_shape=(timesteps, input_dim)))

LSTM을 GRU로 바꿔주기만 하면 된다.

RNN의 설명을 여기서 마친다.