이전에는 Gradient Descent를 사용해서 parameter를 업데이트하고 Cost Function을 최소화했다. 이번에는 다른 Optimization Method를 통해 속도를 높이고 비용을 최소화하는 알고리즘을 배워보자.

언제나 그랬듯, package먼저 다운받아준다.

Packages

import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets

from opt_utils_v1a import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils_v1a import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from copy import deepcopy
from testCases import *
from public_tests import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

Gradient Descent

가장 간단한 최적화 방법이다. 아래의 파라미터 업데이트 공식을 이용해서 파라미터를 업데이트 해 주는 함수를 만들어보자.

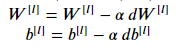
def update_parameters_with_gd(parameters, grads, learning_rate):
    L = len(parameters) // 2
    for l in range(1, L + 1):
        parameters["W" + str(l)] =  parameters["W" + str(l)] - learning_rate*grads['dW' + str(l)]
        parameters["b" + str(l)] =  parameters["b" + str(l)] - learning_rate*grads['db' + str(l)]
    return parameters

이것의 변형으로는 Stochastic Gradient Descent(SGD)와 (Batch)Gradient Descent가 있다. 위에서 만들었던 update_parameter함수는 변하지 않는다. 단지 한번에 한 트레이닝 세트에 대해서 gradient를 계산하게 된다.

하나씩 살펴보자.

(Batch) Gradient Descent

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range (0, num_iterations):
    a, caches = forward_propagation(X, parameters)
    cost+ = compute_cost(a,Y)
    grads = backward_propagation(a, caches, parameters)
    parameters = update_parameters(parameters, grads)

Stochastic Gradient Descent

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range (0, num_iterations):
    for j in range (0,m):
        a, caches = forward_propagation(X, parameters)
        cost+ = compute_cost(a,Y)
        grads = backward_propagation(a, caches, parameters)
        parameters = update_parameters(parameters, grads)

두개의 gradient descent 방식을 비교해보자. Stochastic gradient descent에서는 가중치를 업데이트 하기 전에 오직 한 개의 트레이닝 샘플만 사용한다. 만약에 트레이닝 세트가 너무 크면, Stochastic Gradient Descent가 더 빠를 수 있다. 하지만 parameter들은 min을 향해 "진동"할 수 있다. 그림으로 확인해보자.

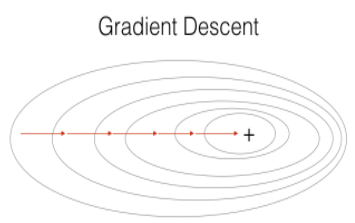
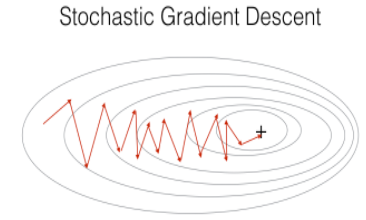
SGD는 위아래로 진동하긴 하지만, 한 가지의 샘플만 사용하기 때문에 각 스탭을 진행하는데에는 GD보다 훨씬 빠른 속도를 가지고 있다.

이 두 방법을 사용하지 않더라도, Mini-Batch Gradient Descent를 사용할 수 있다.

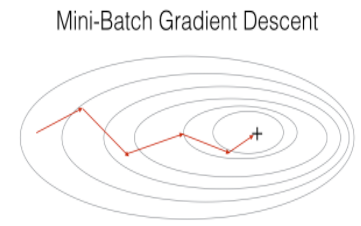
개별적인 트레이닝 샘플에 대해 반복하지 않더라도 mini-batches들을 반복하면서 더 빠른 결과를 얻을 수 있다. 아래에서 더 자세히 다뤄보겠다.

Mini-Batch Gradient Descent

Mini-batch를 만들기 위해서는 두 가지의 할일이 있다.

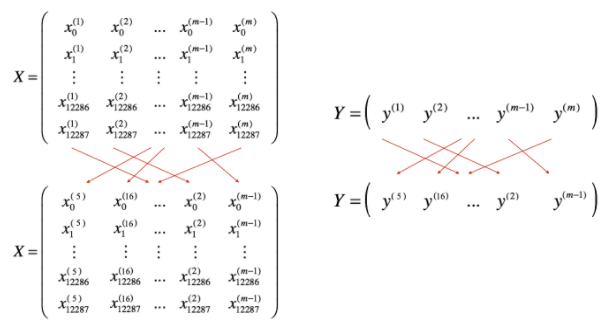
• 섞기
  먼저 X와 Y를 마구 섞어줘야한다. 아래 그림처럼 섞었을 때 나중에 mini-batch로 나눴을 때 랜덤으로 각각 다른 미니배치로 들어가게 된다.
  
• 분할
  섞은 데이터를 mini_batch_size로 나눠준다. 항상 mini_batch_size로 나누는 건 아니지만 여기서는 이렇게 하겠다. 마지막 미니배치는 미니배치사이즈보다 작을 수 있다 (나머지처럼). 그렇다면 아래 그림처럼 된다.
  

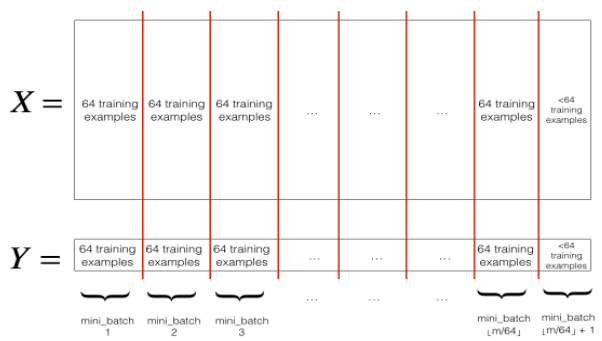
빌드업 하기 전에, mini_batch_X에 대한 예시를 살펴보자.
첫번째 미니 배치와 두번째 미니 배치는 이렇게 작성할 수 있다.
first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
이 부분을 참고해서 작성해보자.

def rendom_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    np.random.seed(seed)
    m = X.shape[1]          #샘플 개수
    mini_batches = []
    
    #섞어주기
    permutation = list(np.random.permutation(m))   #순열
    shuffled_X = X[:,permutation]
    shuffled_Y = Y[:,permutation].reshape((1,m))
    
    inc = mini_batch_size
    
    #분할해주기
    num_complete_minibatches = math.floor(m/mini_batch_size)
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k*inc:(k+1)*inc]
        mini_batch_Y = shuffled_Y[:, k*inc:(k+1)*inc]
        
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)
        
    if m % mini_batch_size ! = 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches*inc:]
        mini_batch_Y = shuffled_Y[:, numcomplete_minibatches*inc:]
        
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.appendd(mini_batch)
        
    return mini_batches

참고로 mini_batch의 사이즈는 2의 제곱수로 많이 나타낸다. 16, 32, 64, 128 등등...

숫자들을 입력하고 출력한다면,

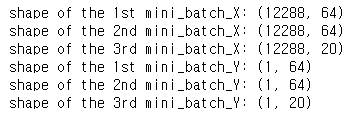
이런 결과를 얻을 수 있다. 1번째 미니배치엔 64개, 2번째도 64개, 마지막 미니배치는 20개가 들어있다.

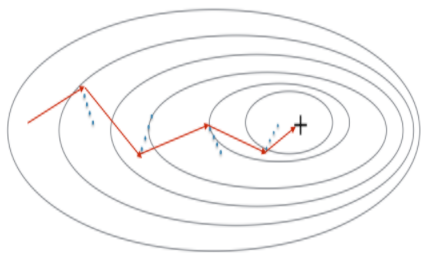
Mini-batch gradient descent는 일부 샘플만 확인하고 parameter들을 업데이트 하기 때문에 업데이트 방향에서 아래처럼 "진동"이 발생한다.

아래에서 설명하는 Momentum을 사용하면 이런 진동을 줄일 수 있다.

Momentum

Momentum은 보다 진동을 없애주기 위해 과거의 기울기를 고려한다. 이전 gradient의 방향은 변수v에 저장되고, 이전 단계 가중치의 평균이 된다. v는 동시에 언덕의 경사나 방향에 따라 속도와 Momentum을 증가시키며 언덕을 내려가는 "속도"라고 생각할 수도 있다.

맨 처음 작업으로 v를 초기화하는 함수를 만들어보자.
v는 0으로 초기화 되어야 하며, dW는 parameter Wl과 같은 shape이어야 한다.

def initialize_velocity(parameters):
    L = len(parameters)//2    #레이어 개수
    v = {}
    
    for l in range(1, L+1):
        v["dW" + str(l)] = np.zeros(parameters["W" + str(l)].shape)
        v["db" + str(l)] = np.zeros(parameters["b" + str(l)].shape)
    return v

0들로 채워진 모습이다.
이번에는 Momentum에서 parameter들을 업데이트 해보자.
아래 공식에서 L은 레이어 개수, 베타는 Momentum, 알파는 learning_rate이다.

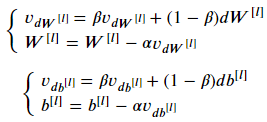
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
    L = len(parameters) // 2     #레이어 개수
    
    for l in range(1, L+1):
        v["dW" + str(l)] = beta*v["dW" + str(l)] + (1-beta)*grads['dW' + str(l)]
        v["db" + str(l)] = beta*v["db" + str(l)] + (1-beta)*grads['db' + str(l)]
        
        parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate*v["dW" + str(l)]
        parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate*v["db" + str(l)]
    
    return parameters, v

숫자들을 대입하고 업데이트 해 보자.

parameter들이 업데이트 되었다.

위에서 언급했다시피, 여기서 베타는 Momentum이다. 만약 베타가 0이라면 표준의 gradient descent가 된다.
그렇다면 베타는 어떻게 고를까?
베타가 클수록 업데이트는 더 부드러워(smoother)진다. 이유는 그만큼 과거의 gradient를 더 많이 고려하기 때문이다. 만약 베타가 너무 크면 업데이트가 너무 원활해질 수 있다.
보통 베타는 0.8에서 0.999사이의 값으로 한다. 0.9가 합리적인 기본값인 경우가 많다. 그래도 Cost function을 줄이기 위해 다양한 베타값과 learning_rate값을 시도해보는 것을 추천한다.

다음으로 Adam에 대해서 알아보자.

Adam

Adam은 RMSprop과 Momentum의 아이디어를 섞은 가장 효과적인 optimization algorithm이다.

• Adam은 Momentum과 같이 이전 gradients을 v에 저장해놓는다. 그리고 bias correction을 거친 v_corrected를 만든다.
• 이전 gradient의 루트값의 평균을 s에 저장해 놓는다. 동시에 bias correction을 거친 s_corrected에 저장한다.
• 위 두개를 합쳐서 parameter들을 업데이트한다.

아래 공식을 따른다.

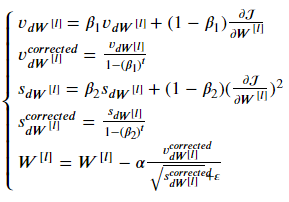
여기서 t는 Adam이 실행된 횟수이다.
L은 레이어 수,
베타1과 베타2는 각각 v와 s를 조절하는 hyperparameters이다.
알파는 learning_rate,
입실론은 0보다 아주 조금 큰 숫자이다.

초기화부터 시작하자.
Momentum과 같이 각각 parameters["W" + str(l)]의 크기와 같게 0으로 초기화해주면 된다.

def initialize_adam(parameters):
    L = len(parameters) // 2
    v = {}
    s = {}
    
    for l in range(1, L+1):
        v["dW" + str(l)] = np.zeros(parameters["W" + str(l)].shape)
        v["db" + str(l)] = np.zeros(parameters["b" + str(l)].shape)
        s["dW" + str(l)] = np.zeros(parameters["W" + str(l)].shape)
        s["db" + str(l)] = np.zeros(parameters["b" + str(l)].shape)
    
    return v, s

0으로 초기화 한 모습이다.
이제 parameter들을 업데이트 시켜주자.
위에서 설명했던 공식을 다시 가져와보자.

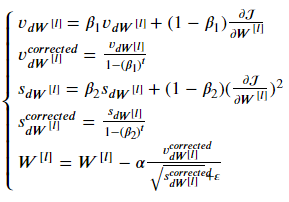
이대로 함수를 만들어주면 된다.

def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01, beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}
    
    for l in range(1, L+1):
        v["dW" + str(l)] = beta1*v["dW" + str(l)] + (1-beta1)*grads['dW' + str(l)]
        v["db" + str(l)] = beta1*v["db" + str(l)] + (1-beta1)*grads['db' + str(l)]
        
        v_corrected["dW" + str(l)] = v["dW" + str(l)]/(1-beta1**t)
        v_corrected["db" + str(l)] = v["db" + str(l)]/(1-beta1**t)
        
        s["dW" + str(l)] = beta2*s["dW" + str(l)] + (1-beta2)*grads['dW' + str(l)]*grads['dW' + str(l)]
        s["db" + str(l)] = beta2*s["db" + str(l)] + (1-beta2)*grads['db' + str(l)]*grads['db' + str(l)]
        
        s_corrected["dW" + str(l)] = s["dW" + str(l)]/(1-beta2**t)
        s_corrected["db" + str(l)] = s["db" + str(l)]/(1-beta2**t)
        
        parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate*v_corrected["dW" + str(l)]/(np.sqrt(s_corrected["dW" + str(l)])+epsilon)
        parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate*v_corrected["db" + str(l)]/(np.sqrt(s_corrected["db" + str(l)])+epsilon)
        
    return parameters, v, s, v_corrected, s_corrected

t, learning_rate, beta1, beta2, epsilon에 각각 값을 넣어주고 실행시켜 아래처럼 parameter값들을 뽑아낼 수 있다.

Model with different Optimization algorithms

아래에서는 "moons"라는 데이터셋으로 각각 다른 optimization 방법들을 테스트 해 볼 것이다. 이 데이터셋은 초승달 두개가 겹쳐 보인다고 해서 "moons"라 불린다.

어떻게 생겼는지 데이터를 불러오며 확인해보자.

train_X, train_Y = load_dataset()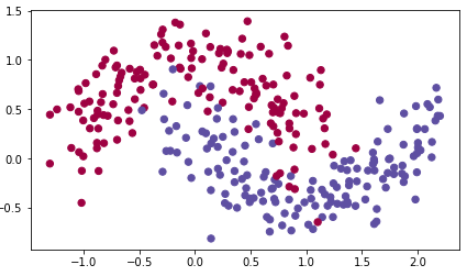

아래 모델 함수에서는 위에서 만들었던 함수들을 사용할 것이다.
모두
update_parameters_with_gd() : Mini-batch gradient descent
initialize_velocity(), update_parameters_with_momentum() : Mini-batch Momentum
initialize_adam(), update_parameters_with_adam() : Mini-batch Adam
이다.

모델함수를 빌드해보자.

def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9, beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 5000, print_cost = True):
    L = len(layers_dims)
    costs = []
    t = 0
    seed = 10
    m = X.shape[1]
    
    parameters = initialize_parameters(layers_dims)
    
    if optimizer == "gd":
        pass     #초기화 필요없음
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)
    elif optimizer == "adam":
        v,s = initialize_adam(parameters)
    
    for i in range(num_epochs):
        seed = seed+1
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
        cost_total = 0
        
        for minibatch in minibatches:
            (minibatch_X, minibatch_Y) = minibatch
            a3, caches = forward_propagation(minibatch_X, parameters)
            cost_total += compute_cost(a3, minibatch_Y)
            grads = backward_propagation(minibatch_X, minibatch_Y, caches)
            if optimizer == "gd":
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
            elif optimizer == "adam":
                t = t + 1 # Adam counter
                parameters, v, s, _, _ = update_parameters_with_adam(parameters, grads, v, s,
                                                               t, learning_rate, beta1, beta2,  epsilon)
        cost_avg = cost_total / m
        
        # Print the cost every 1000 epoch
        if print_cost and i % 1000 == 0:
            print ("Cost after epoch %i: %f" %(i, cost_avg))
        if print_cost and i % 100 == 0:
            costs.append(cost_avg)
                
    # plot the cost
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters

이제 각각 다른 세개의 optimization방법으로 3-레이어 모델을 돌려보자.

Mini-Batch Gradient Descent

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)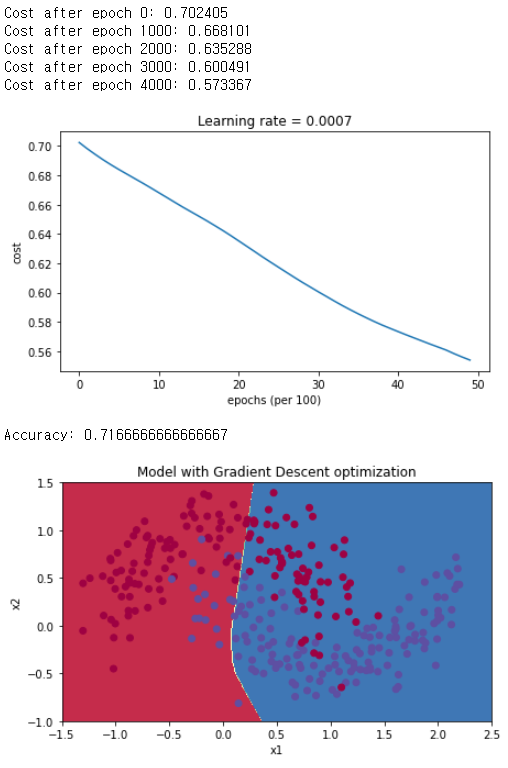

Mini-Batch Gradient Descent with Momentum

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)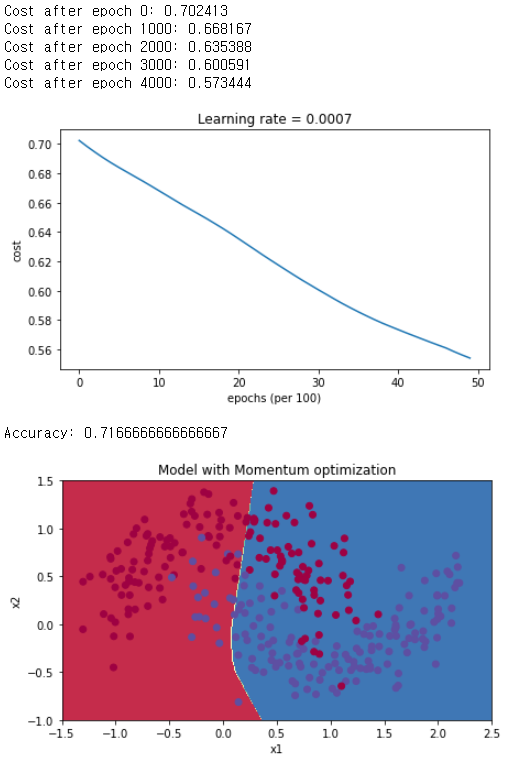

Mini-Batch with Adam

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)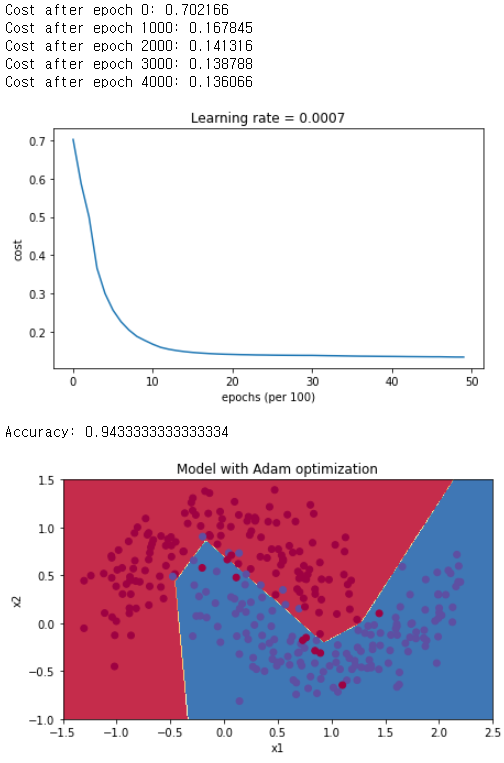

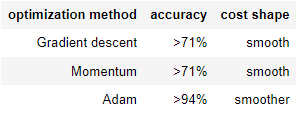
Analysis

Adam에 관련된 논문은 여기서 확인할 수 있다.

Learning Rate Decay and Scheduling

지금까지 베타값을 조절하는 방법에 대해서 언급했다. 이번에는 또 다른 hyperparameter인 learning rate에 대해 알아보자.
learning rate가 크다면 보폭이 크다고 생각하면 된다. 보폭이 크면 우리가 원하는 최소값에 도달하기 힘들고, 어쩌면 그 주위를 계속 맴돌게 될 수도 있다. learning rate값을 서서히 낮추면 더 작은 보폭으로 점점 최솟값에 가까워 질 수 있다. 이 아이디어가 바로 Learning Rate Decay의 아이디어이다.

이제 방금 설명한 세 가지의 다른 optimizer method에서 다른 learning rate로 인해 어떻게 값이 바뀌는지 확인해보자.

여기엔 learning rate decay라는 개념 이외에도 decay와 decay_rate라는 parameter들이 새로 등장한다.

모델을 빌드해보자.

def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8, num_epochs = 5000, print_cost = True, decay=None, decay_rate=1):
    
    L = len(layers_dims)
    costs = []
    t = 0
    seed = 10
    m = X.shzpe[1]
    lr_rates = []
    learning_rate0 = learning_rate
    
    parameters = initialize_parameters(layers_dims)
    
    if optimizer == "gd":
        pass
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)
    
    for i in range(num_epochs):
        seed = seed + 1
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
        cost_total = 0
        
        for minibatch in minibatches:
            (minibatch_X, minibatch_Y) = minibatch
            a3, caches = forward_propagation(minibatch_X, parameters)
            cost_total += compute_cost(a3, minibatch_Y)
            grads = backward_propagation(minibatch_X, minibatch_Y, caches)
            
            # Update parameters
            if optimizer == "gd":
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
            elif optimizer == "adam":
                t = t + 1 # Adam counter
                parameters, v, s, _, _ = update_parameters_with_adam(parameters, grads, v, s,
                                                               t, learning_rate, beta1, beta2,  epsilon)
        cost_avg = cost_total / m
        if decay:
            learning_rate = decay(learning_rate0, i, decay_rate)
        # Print the cost every 1000 epoch
        if print_cost and i % 1000 == 0:
            print ("Cost after epoch %i: %f" %(i, cost_avg))
            if decay:
                print("learning rate after epoch %i: %f"%(i, learning_rate))
        if print_cost and i % 100 == 0:
            costs.append(cost_avg)
                
    # plot the cost
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters

learning rate를 저하시키기 위해서 "exponential learning rate decay"를 시도할 것이다. 아래와 같은 수식을 갖는다.

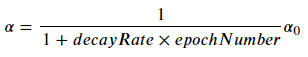
learning_rate를 업데이트 해 주는 함수를 만들자.

def update_lr(learning_rate0, epoch_num, decay_rate):
    learning_rate = 1/(1+decay_rate*epoch_num)*learning_rate0
    
    return learning_rate

아래는 업데이트 한 모습이다.

learning_rate = 0.5
print("Original learning rate: ", learning_rate)
epoch_num = 2
decay_rate = 1
learning_rate_2 = update_lr(learning_rate, epoch_num, decay_rate)

print("Updated learning rate: ", learning_rate_2)

이렇게 업데이트가 된다.
이번엔 Gradient Descent로 3-레이어 모델을 학습시키고, 예측하고 그래프로 나타내보자.

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd", learning_rate = 0.1, num_epochs=5000, decay=update_lr)

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)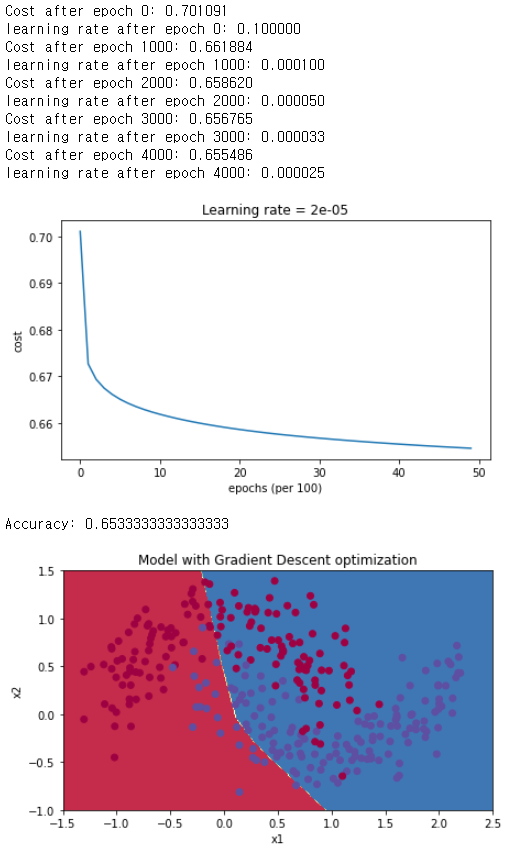

매번 learning rate decay를 설정하면 learning rate가 너무 빨리 0에 가까워지게 된다.
적은 epoch에 대해서는 문제가 크게 발생하지 않는다. 그러나 epochs가 많을수록 optimization algorithm의 업데이트는 중단될 수 있다. 이런 문제의 해결 법 중 하나는 몇 단계마다 learning rate를 decay해주는 것이다. 이것을 fixed interval scheduling이라고 부른다.

Fixed Interval Scheduling

이것을 이용해서 learning rate를 다시 계산해보자.
새로운 공식이 등장한다.

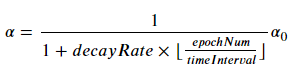
여기서 꼭 주의해야 할 점은

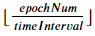
이 부분을 np.floor를 이용해서 정수값을 내 줘야 한다는 것이다! np.floor에 대한 설명은 여기를 참고하자.

def schedule_lr_decay(learning_rate0, epoch_num, decay_rate, time_interval=1000):
    learning_rate = learning_rate0/(1+decay_rate*np.floor(epoch_num/time_interval))
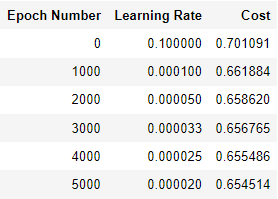
    return learning_rate

변수를 만들어주고 출력해주자. 원래 lr, 10번의 epoch후 lr, 100번의 epoch후 lr을 출력한다.

learning_rate = 0.5
print("Original learning rate: ", learning_rate)

epoch_num_1 = 10
epoch_num_2 = 100
decay_rate = 0.3
time_interval = 100
learning_rate_1 = schedule_lr_decay(learning_rate, epoch_num_1, decay_rate, time_interval)
learning_rate_2 = schedule_lr_decay(learning_rate, epoch_num_2, decay_rate, time_interval)
print("Updated learning rate after {} epochs: ".format(epoch_num_1), learning_rate_1)
print("Updated learning rate after {} epochs: ".format(epoch_num_2), learning_rate_2)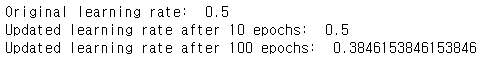

위와 같은 learning rate값을 얻는다.

Using Learning Rate Decay for each Optimization Method

이번엔 각각의 Optimization method에 Learning rate decay를 적용시켜보자.

Gradient Descent

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd", learning_rate = 0.1, num_epochs=5000, decay=schedule_lr_decay)

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)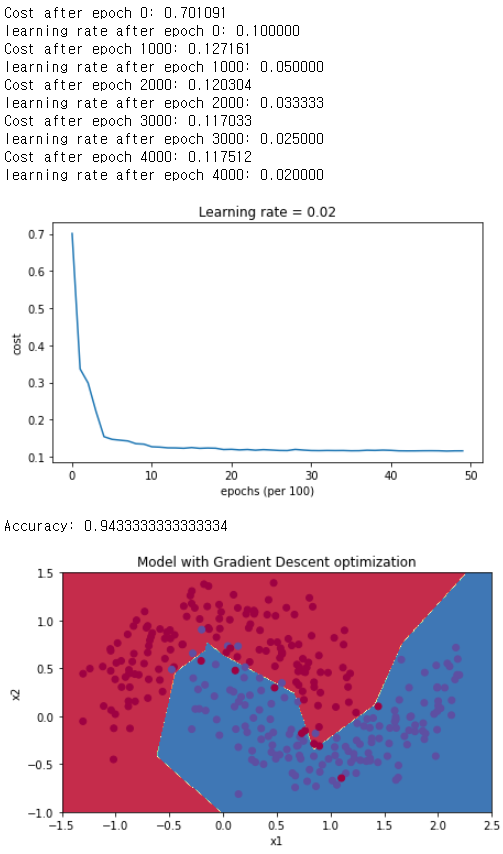

Gradient Descent with Momentum

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "momentum", learning_rate = 0.1, num_epochs=5000, decay=schedule_lr_decay)

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Gradient Descent with momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)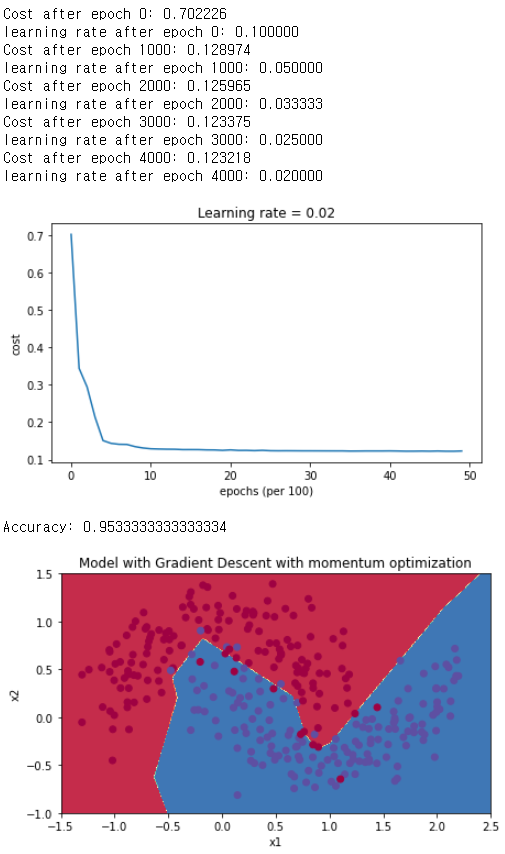

Adam

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam", learning_rate = 0.01, num_epochs=5000, decay=schedule_lr_decay)

# Predict
predictions = predict(train_X, train_Y, parameters)

# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)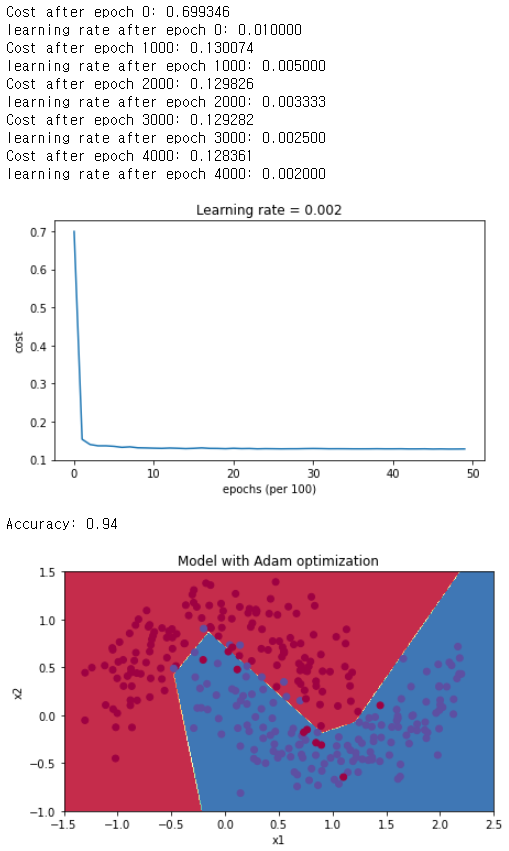

Analysis

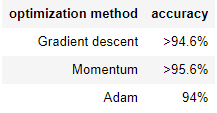
아까 분석때는 Adam의 정확도가 훨씬 높았는데, learning rate decay를 적용하고 난 후에는 두개의 방법 다 Adam과 비슷해졌다는 것을 발견할 수 있다.

Adam의 경우 정확도는 비슷할지 몰라도, 속도는 확실히 빨라졌다.

여기서 Optimization method에 대한 설명을 마친다.