1. Introduction

reject option이라고 불리는 selective prediction의 문제를 deep neural network에서 고려하고 integrated reject option을 가진 deep neural architecture인 SelectiveNet를 제안한다.

기존의 rejection 메커니즘들은 대부분 미리 훈련된 network의 prediction confidence에서 threshold로 수행되는데, SelectiveNet은 classification과 rejection을 동시에 최적화하면서 훈련이 됨

reject option은 크게 두 가지 아이디어로 나뉜다.

1) cost-based model: selective moel이 abstention에 대한 cost를 track하는 loss function을 최소화하게끔 하는 cost-based model
2) 나머지는 prediction confidence에 대한 proxy를 serve하는 function에서 built됨

2. Selective Prediction Problem Formulation

f는 prediction function, g는 X -> {0, 1}인 selective function일 때, selective model은 다음과 같은 binary qualifier로 표현됨

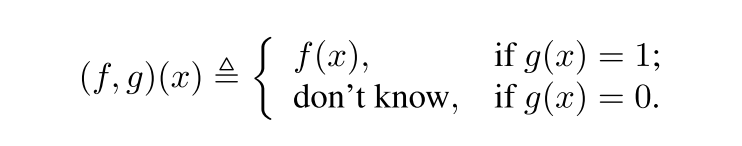
selective model의 성능은 coverage와 risk로 수치화되는데, coverage는 다음과 같이 non-rejected region의 probability mass로 정의됨

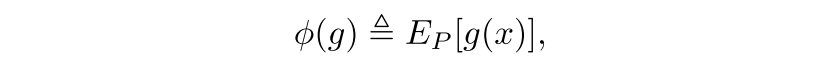
(f, g)의 selective risk는 다음과 같이 정의되는데, coverage에 대한 trade-off가 발생한다.

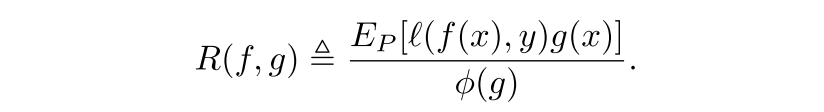
true selective risk와 true coverage는 any given labeled set S_m에 대해서 계산될 수 있는 각각의 empricial counterparts를 가짐

empirical selective risk (non-rejected xi에 대해서만 loss를 평균한 것을 empirical coverage로 나눈 것, empirical coverage가 1이면 full coverage로 non-selective한 상황으로 그냥 loss와 같음)

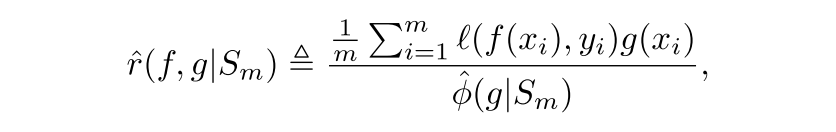
empirical coverage, Sm에 대해서 각 xi에 대한 selective function g의 평균.. 실제로 어느정도 비율로 cover했냐 (1이면 non-selective한 상황임)

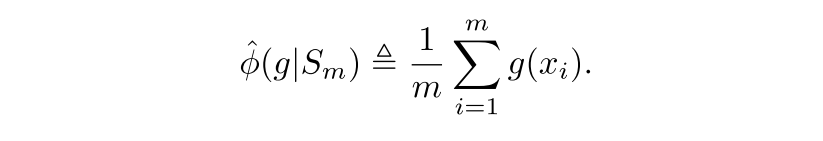
optimal selective model은 coverage에 대한 constraint를 주고 selective rick를 최적화하거나 반대로 (risk에 constraint) 최적화하는 것으로 정의될 수 있는데, 여기선 coverage에 constraint를 주는 쪽으로 함. 0 < c <= 1이고 hypothesis class $\Theta$일 때, optimal selective model은 다음과 같음

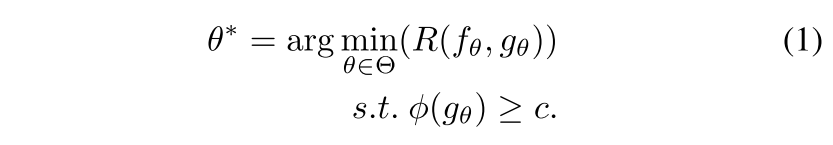
$\Theta$는 f와 g에 대해 주어진 deep network architecture에 대한 파라미터 집합

3. Related Work

reject option techniques에 대한 문헌은 매우 광범위, 주로 hypothesis class와 SVM, nearest neighbours, boosting와 같은 알고리즘을 학습하는 것에 집중하였음.

selective predictor를 build하는 흔한 방식은 이미 훈련된 모델에 selection mechanism을 더하는 것

다른 방식으로 "Learning with rejection"는 predictor와 selection function을 jointly 학습하도록 제안했는데 이 연구에서 이런 방식을 따른다.

NN에 selective prediction을 고려할 때, straightforward하고 effective한 기술은 이미 모든 point에 대해 최적화되어있는 미리 훈련된 net으로부터 나온 confidence score에 대해 threshold를 설정하는 것. "Selective classification for deep neural networks"은 이를 DNN으로 확장해서 confidence score로부터 어떻게 selective classifier를 유도하는지 보여줬다.

이후 연구들에서는 NN으로부터 confidence score를 추출하는 두 가지 기술에 대해 의논된다.

첫번째는 Softmax Response (SR), maximal activation in the softmax layer
두번째는 Monte-Carlo droput (MC-dropout) proposed by "Dropout as a bayesian approximation: representing model uncertainty in deep learning", dropout이 적용된 network를 여러 번 feed-forward시켜 나온 통계값을 사용하는 것으로 single net에서 confidence score를 추출하는 유일한 non-Bayesian technique. 하지만, 여러 번 뽑다보니 cost가..

confidence score function의 다른 family는 multiple model의 ensemble에서의 통계값을 사용하는 것이 있는데 이 연구에서는 selective classifier의 ensemble이 결과를 더 향상시킬 것이라고 noting하면서 single classifier에서의 selective classification에 focus한다.

4. SelectiveNet

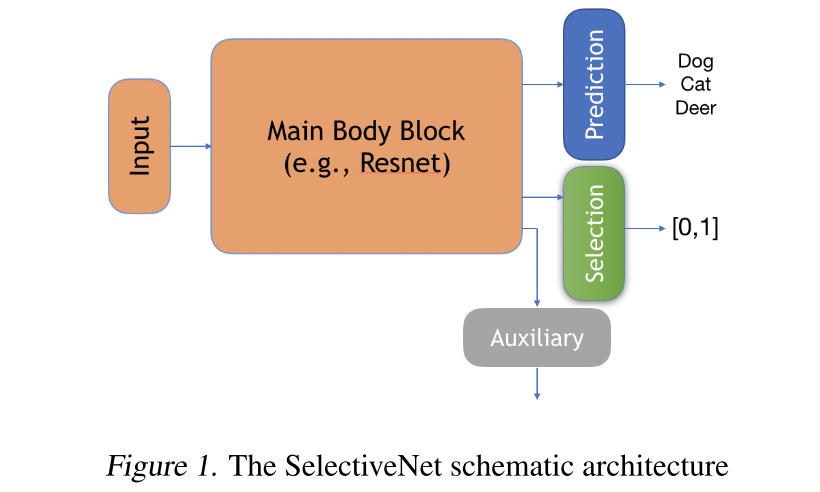
SelectiveNet Architecture

3 output heads

• prediction (depending on the application, softmax or linear)
• selection (final layer is a single neuron with a sigmoid activation)
• auxiliary (prediction과 같은 task에 standard loss function 학습)

SelectiveNet Optimization

coverage constraint를 enforce하기 위해 잘 알려진 Interior Point Method (IPM)의 variant를 적용함. 그러면 S_m의 sample들에 걸친 평균이 되는 다음의 unconstrained objective를 만듬

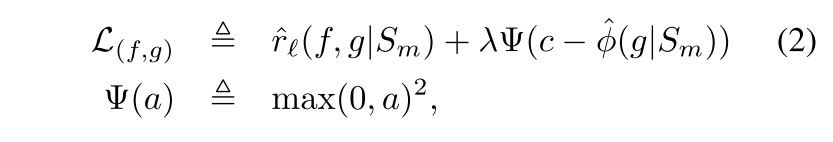
c는 target coverage고 $\lambda$는 constraint의 상대적 중요성을 제어하는 hyperparameter고 $\Psi$는 quadratic penalty function

auxiliary head, h는 f에 할당된 똑같은 prediction task를 standard loss function으로 풀도록 훈련됨

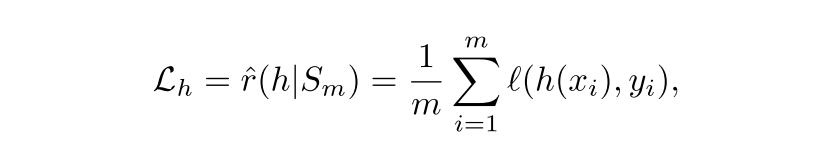
overall training objective는 다음과 같음

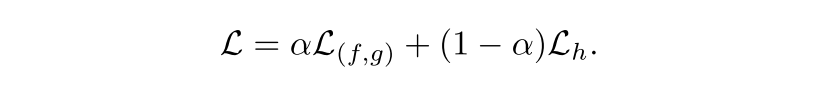
L_h가 없으면 정확한 low-level feature가 만들어지기 전에 훈련셋의 fraction c에 focus하게 되고 훈련 셋의 잘못된 subset에 overfit되는 경향이 발생할 것이다.

alpha가 너무 작게 설정하면, SelectiveNet은 poor selective risk를 초래할 것이다.
모든 실험에서 alpha는 0.5로 설정했음

5. Coverage Accuracy

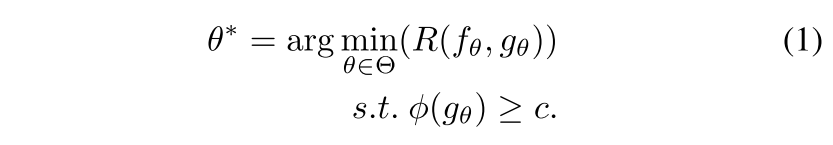
Eq 1와 같이 constrained ERM (Empirical risk minimization)을 학습할 때, test set에서는 constraint를 위반할 것을 예상할 수 있음

여기에선 이건 실제 coverage $\theta(g)$가 요구되는 target coverage c보다 작을 수 있음을 의미함

반면에 constraint가 위반하지 않더라도 sub-optimal model인 (f, g)에 취약하다?

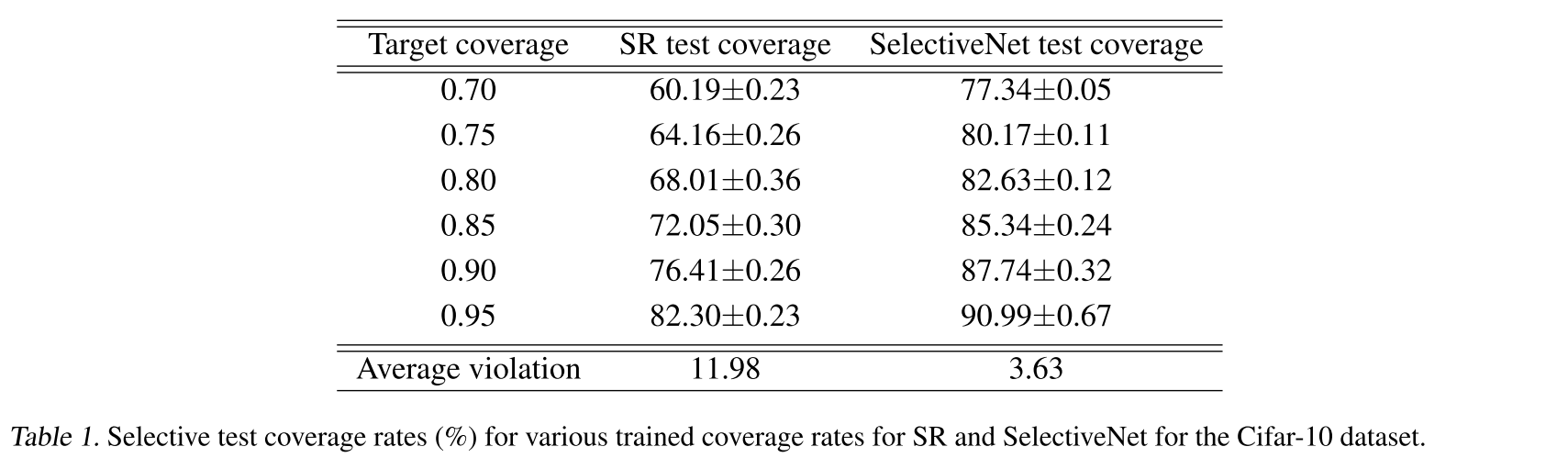
SelectiveNet이 SR보단 coverage accuracy가 확실히 높으나 가능한 target coverage에 가까운 test coverage를 가지는 selective model을 만드는 거에 관심이 있음

간단한 post-training coverage calibration 기술로 쉽게 달성될 수 있음

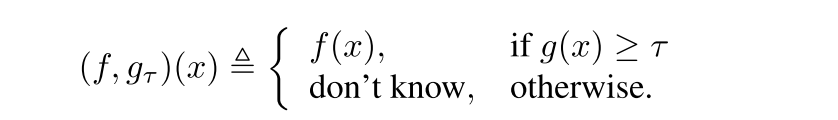
주어진 unlabeled validation set V_n에서 $\tau$는 g(xi)의 100(1-c)%.

g(xi) >= $\tau$는 Bernoulli variable임을 알면 Hoeffding bound를 바로 적용할 수 있음. to bound the probability of (double sided) coverage violation greater than $\epsilon$

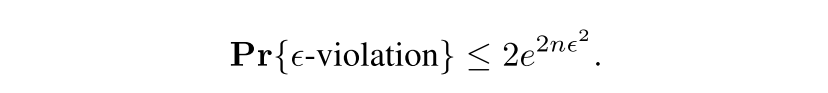
6. Experiment design and details

dataset

Street View House Numbers - 10 classes, 32 x 32 x 3
CIFAR-10 - 10 categories, 32 x 32 x 3
Cats VS Dogs (from ASIRRA dataset) - 2 classes, 64 x 64 (from 360 x 400)
Concrete Compressive Strength (from UCI repository) - 8 features (7 its ingredients and age), 1 target value (compressive strength)

baseline models

Softmax Response (SR)
Monte Carlo-dropout (MC-Dropout) - classification: dropout (p=0.5), 100 feed-forward MC iterations / regression: dropout (p=0.05), 200 iterations

architectures and hyperparameters

VGG-16을 썼는데, 바뀐 점은 (i) only one fully connected layer with 512 neurons (original one has two fully connected layers of 4096 neurons), (ii) batch normalization, (iii) dropout 사용

data aug.: horizontal flips, vertical and horizontal shifts, and rotations

SGD with a momentum of 0.9, initial learning rate of 0.1, and a weight decay of 5e-4. The learning rate was reduced by 0.5 every 25 epochs, and trained fro 300 epochs

full coverage validation accuracy: 96.79% for SVHN, 93.21% for Cifar-10 and 96.42% for Cats vs. Dogs.

7. Experiments

Selective Classification

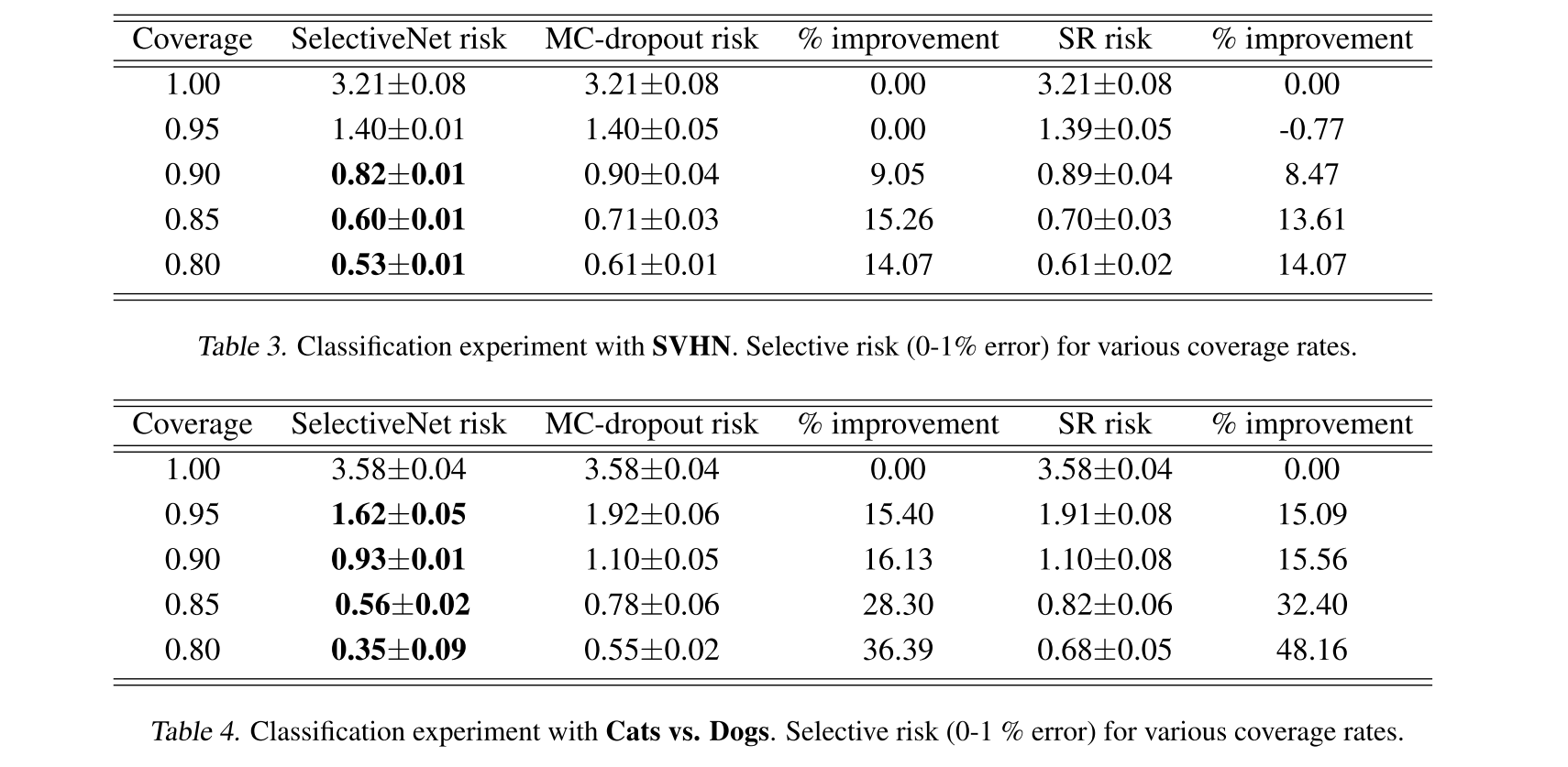
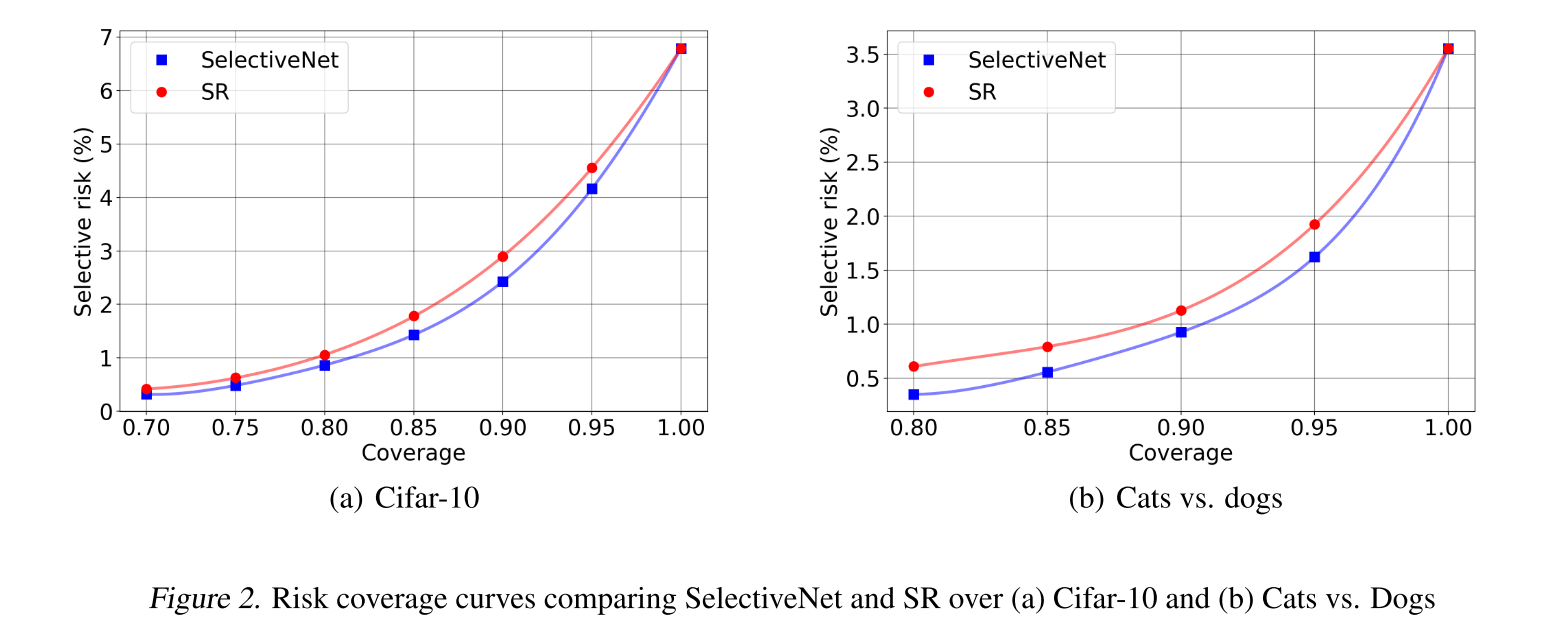
Selective Regression

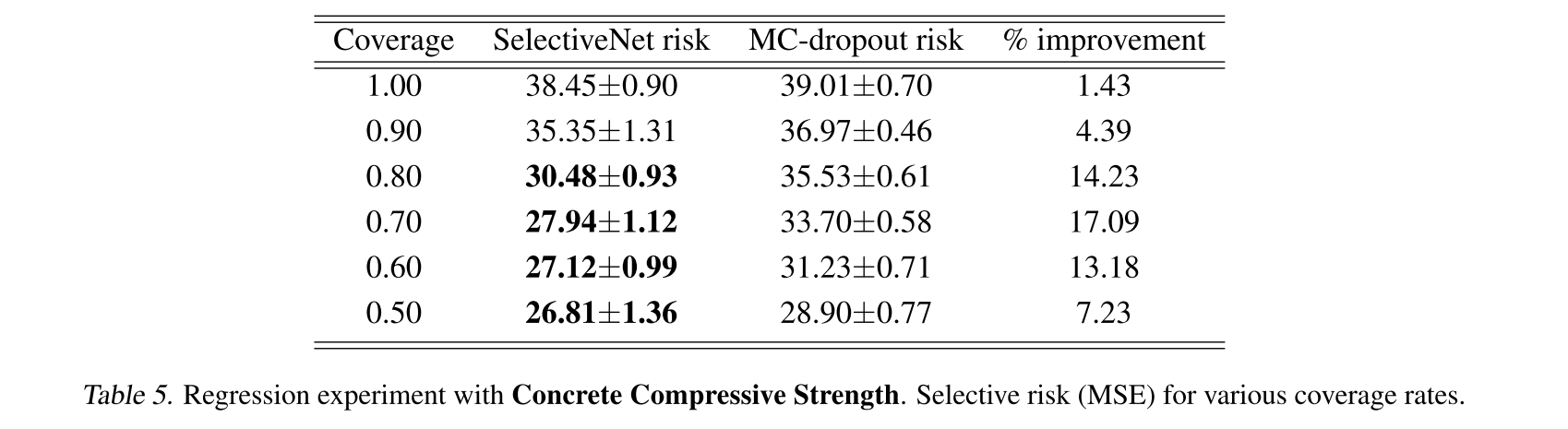
risk는 selective prediction에서의 loss와 같으므로 낮을수록 좋은 거 ㅇㅇ

8. Empirical Observations

Coverage Calibration

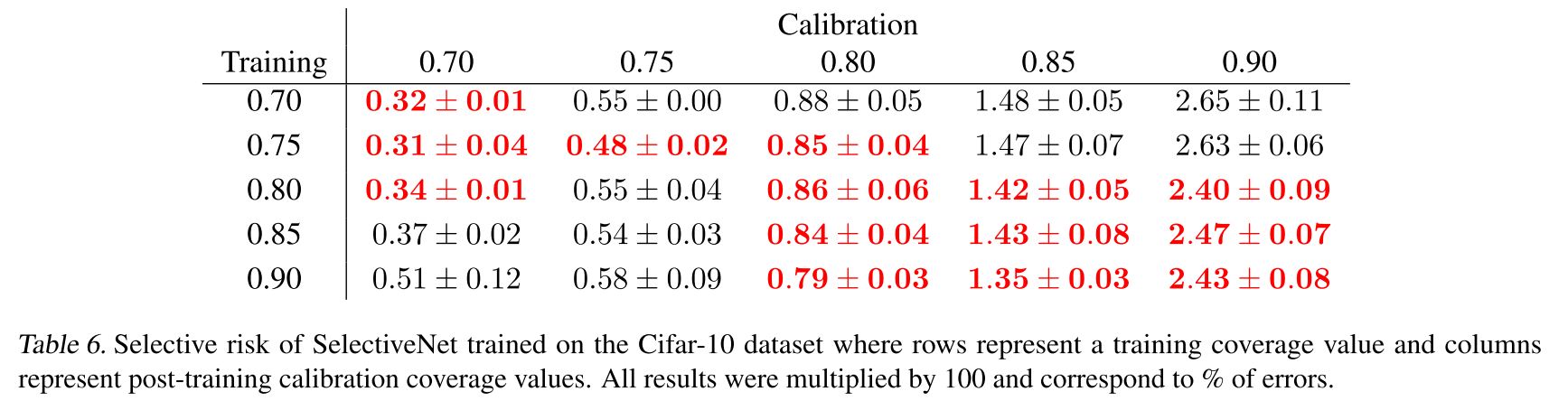
diagonal이 가장 성능이 좋은 게 당연하지만, off-diagonal 다른 coverage로 훈련한 모델들도 특정 coverage로 calibration함으로써 유사한 성향으로 risk가 떨어지거나 오르더라

"The fact that the off-diagonal elements often tend to admit inferior selective risks indicates that the calibrated SelectiveNet effectively optimizes its coverage-specific selective risk."

Learned Representation

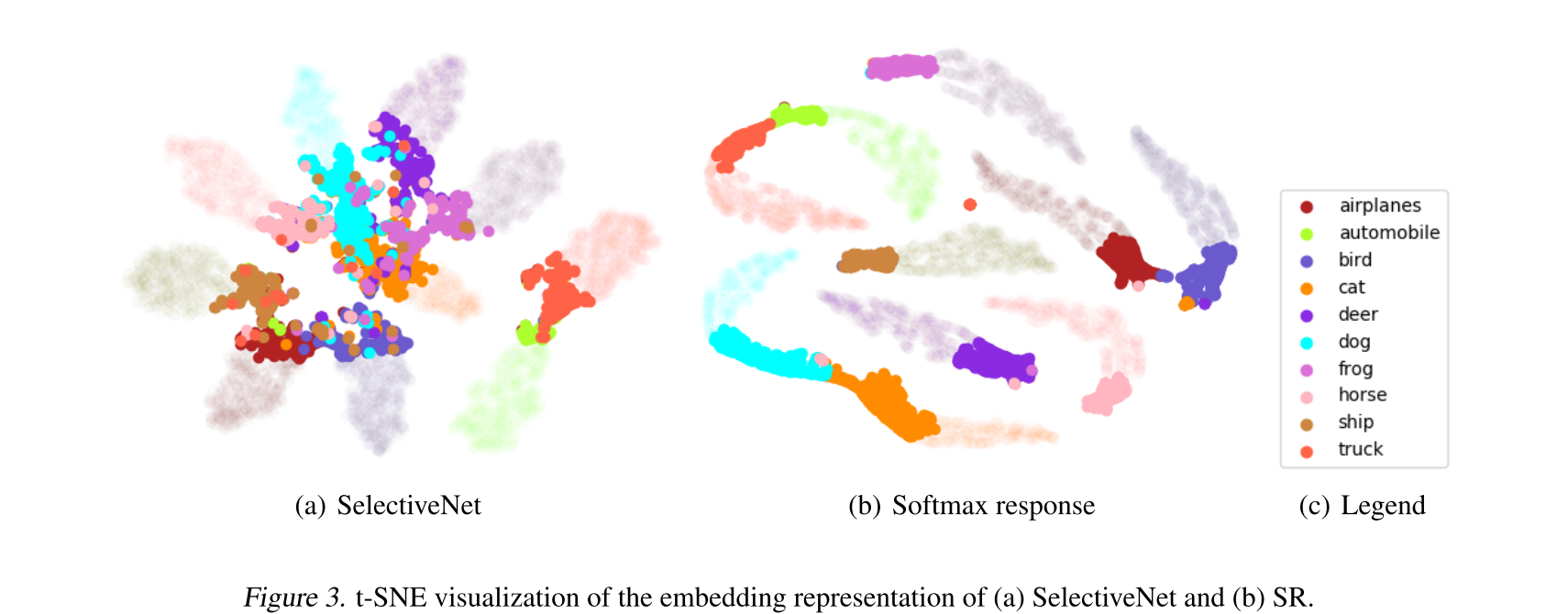
Rejected된 게 bold dots

SR을 보면 rejected끼리도 well-separated되어있는데, SelectiveNet은 rejected를 나누는데 representational capacity를 낭비하지 않았다?

그리고 중앙에 모여있는 구조는 selection function g에 capture되기 더 쉽게 만들 수 있다

9. Concluding Remarks

동일 네트워크 안에서 selection과 prediction 모델들의 mutual training을 하는 이 새로운 모델은 모델이 reject되지 않을 가장 관련있는 instance에 focus하도록 강제하는 이점을 가진다.

그리고 regression에서는 성능이 좋은 것뿐만 아니라 가장 빠르므로 fast inference를 요구하는 deep regression (visual tracking or detection 등) 적용에서 사용해볼만하다.